Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский кооперативный институт (филиал РУК)

Предмет:

Макроэкономическое планирование и прогнозирование

Файл:

МатАн_ЛинАлг_080100 / ПланыПЗ_МА_080100.pdf

Скачиваний:

Добавлен:

26.02.2016

Размер:

496.78 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Тема 8. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов

8.1. Типовые примеры

Пример 8.1.1. Вычислить интеграл ∫3 x +1 dx .

Решение. Найдем первообразную функции 3 x +1 и вычислим интеграл

7			33	(x +1)	4		7		3					45
7					4
∫	3	x +1 dx =									4	4
								=		2		−1	=		.
				4				=	4	2		−1	=	4	.
0				4			0		4					4
							π
Пример 8.1.2. Вычислить интеграл ∫4								(1 − x)sin 2xdx .
						0

Решение. Применив формулу интегрирования по частям, получим

			π										u =1 − x									dv = sin 2xdx
		4											u =1 − x									dv = sin 2xdx
			∫(1 − x)sin 2xdx =																								1					=
			∫(1 − x)sin 2xdx =																			v = −					1		cos 2x			=
		0											du = −dx									v = −					2		cos 2x
																											2
									π		π																									π
					1				π		4		1												1						1					π
				−					4	−	4			cos 2xdx							= 0		+				cos0 −					sin 2x				4	=

= (1 − x)					2	cos 2x					∫		2												2						4
					2						∫		2												2						4
									0		0																									0
							=		1	−	1 sin					π		=		1 −		1 =		1 .
									2		4					2				2		4		4
																			4		xdx
Пример 8.1.3. Вычислить интеграл ∫																					xdx			.
Пример 8.1.3. Вычислить интеграл ∫																								.
																			0		x +		1
																			0
Решение.
				x =t2
4	xdx														2		t	2	2tdt				2			2								1
	xdx			dx = 2tdt													t		2tdt							2								1
			=									=										=2		t				− t		+1	−				dt =
∫0 x +			=				t = 0					=			∫0			t	+1			=2		t				− t		+1	−				dt =
∫0 x +		1		x = 0			t = 0								∫0			t	+1				∫0										t +1
							t = 2
				x = 4			t = 2
	t3			t	2	+ t − ln		t +1					2	=2					8	−	2 +									= 2		8		− ln 3
					2

= 2		−																					2 − ln 3														.
	3			2									0						3													3
	3			2									0						3													3

Пример 8.1.4. Найти площадь криволинейной трапеции D , ограниченной

параболой y = 4x − x2 и осью абсцисс y = 0 .
Решение. Построим область	D (рис. 8.1.1). Найдем y
точки пересечения параболы с осью Ox
4x − x2 = 0 x(4 − x) x1 = 0,				0		D
4x − x2 = 0 x(4 − x) x1 = 0,				0			4 x
	x2 = 4.				РИС. 8.1.1
Ветви параболы смотрят вниз.					РИС. 8.1.1
Ветви параболы смотрят вниз.
Получили криволинейную трапецию с основанием [0,4], ограниченную
кривой y = 4x − x2 , y ≥ 0 при x [0,4]. Вычислим ее площадь
S = ∫4 (4x − x2 )dx = 2x2 −		x3	4 =	32 (кв.ед.).
		x3

0	3		0	3
Пример 8.1.5. Вычислить площадь фигуры				D , ограниченной параболой

y = x2 − 2 и прямой y = −x .

Решение. Построим фигуру D (рис. 8.1.2). Найдем абсциссы точек пересечения параболы и прямой. Для этого решим систему уравнений

y = x2 − 2,

y = −x.

Получим

x2 − 2 = −x x2 + x − 2 = 0x1 = −2, x2 =1.

y	y = x2	− 2

–2	y = −x	x
	y = −x	x
	–2
	РИС. 8.1.2

Пределы интегрирования найдены. Это

a = −2

и b =1. Верхняя кривая:

(x)= −x , а нижняя – y

(x)= x2

− 2 . Найдем площадь фигуры D .

S = ∫ −x

− x

+ 2 dx = −

−

−2

1 −

1 + 2 + 2 − 8

1 (кв.ед.)

= −

+ 4 = 4

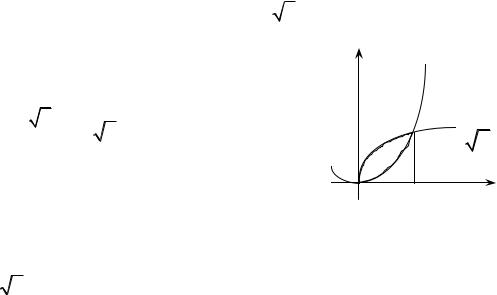
Пример 8.1.6. Найти объем тела, полученного от вращения вокруг оси

Ox фигуры, ограниченной графиками функций y = x, y = x2 .

Решение. Построим чертеж (рис. 8.1.3) и найдем абсциссы точек пересечения кривых:

	x
y =	x	x = x2
		x = x2
y = x2

x = x4 x(1 − x3 )= 0 x1 = 0, x2 =1.

Найдем объем полученного тела вращения:

y = x2

	y =	x
0	1	x
	РИС. 8.1.3

	1			2			2		1						x	2			x		5		1			3
	1			2			2		1							2					5		1
V = π∫ (			x )		− (x2 )			dx	= π∫(x − x4 )dx = π								−							=				π.
V = π∫ (			x )		− (x2 )			dx	= π∫(x − x4 )dx = π								−							=		10		π.
	0								0					2				∞		5			0			10
																		∞				dx
Пример 8.1.7. Вычислить несобственный интеграл ∫																						dx					.
Пример 8.1.7. Вычислить несобственный интеграл ∫																				(1		− x)			3		.
																	3			(1		− x)
Решение.
∞	dx				∞	(1 − x)−3 d (1 − x)= −(1					− x)		−2	∞ =							1						∞ =
∞					∞								−2
∫			= −∫
∫	(1 − x)	3	= −∫								−2							2(1 − x)						2
3	(1 − x)				3						−2			3				2(1 − x)								3
						= lim			1	− 1 = 0	−	1	= −1 .
						= lim			− x)2	− 1 = 0	−		= −1 .
						x→∞ 2(1			− x)2	8		8		8
Интеграл сходится и его значение равно											−	1 .
												8

8.2.Контрольные вопросы

1)Сформулируйте определение определенного интеграла.

2)Перечислите свойства определенного интеграла.

3)Запишите формулу Ньютона-Лейбница.

4)Какой вид имеет формула интегрирования по частям для определенного интеграла?

5)Запишите формулу замены переменной в определенном интеграле.

6)Что называется криволинейной трапецией?

7)Чему равна площадь криволинейной трапеции?

8)Как найти площадь произвольной фигуры D ?

9) Запишите формулу для вычисления объема тела, полученного от вращения криволинейной трапеции D : y = 0 , x = a , x =b , y = y(x) вокруг оси

Ox .

10) Запишите формулу для вычисления объема тела, полученного от враще-
ния плоской	фигуры	D :	x = a, x =b, y = y1	(x), y = y2 (x),
y1 (x)≤ y2 (x),	x [a,b] вокруг оси Ox .

11)Сформулируйте определение несобственного интеграла с бесконечным верхним пределом интегрирования.

12)Какой вид имеет формула Ньютона-Лейбница для вычисления несобственного интеграла?

8.3.Практические задания

8.3.1. Вычислить определенный интеграл, используя формулу Ньютона – Лейбница:

2	(3x2 − x +1)dx ;			4	( x + x x )dx ;	2	5dx
а) ∫				б) ∫		в) ∫	5dx		;
а) ∫				б) ∫		в) ∫	2x +	3	;
−1				0		−1	2x +	3
−1				0		−1
3		dx		π		π
3		dx		5		4
г) ∫1			;	д) ∫sin 5xdx ;		е) ∫sin2 xdx .
г) ∫1		x2 +1	;	д) ∫sin 5xdx ;		е) ∫sin2 xdx .
				0		0

8.3.2. Вычислить определенный интеграл, используя формулу интегрирования по частям:

∫2 xcos xdx ;

б) ∫2 (x + 3)sin xdx ;

а)

в) ∫(

3x + 2)e−xdx ;

г) ∫ln

(x +1)dx .

8.3.3. Вычислить определенный интеграл:

sin xdx

а)

∫

;

б) ∫(ex −1)4exdx ;

в)

∫

dx ;

г)

;

∫1

0 cos x + 3

+1)

1 + ln x

−1

д)

∫

;

е) ∫x3 sin xdx ;

ж)

∫

dx ;

з) ∫

(11 + 5x)

x + x

0 1 + e

−2

8.3.4. Вычислить определенные интегралы методом замены переменной:

xdx

а) ∫

;

б) ∫

;

в) ∫

;

x −1

1 +

1 + x

ln 2

3 cos xdx

г) ∫

;

д) ∫ ex −1dx ;

е) ∫

;

x +1(

x +1

sin

3 xdx

(x +1)dx

ж) ∫

;

з) ∫

;

и) ∫

x( x +

x +1(x −8)

x +

−6

8.3.5. Вычислить площадь криволинейной трапеции, ограниченной линиями:

а) y = x2 , y = 0, x = 2 ;		б) y = 3 ,	y = 0, x =1, x = 2 ;
		x
в) y = x3 , y = 0, x = −1, x =1;		г) y = x2 − 6x, y = 0 ;
д) y = x, xy =1,	y = 0, x = 2 ;	е) y = ln x,	y = 0, y =1, x = 0 .
8.3.6. Вычислить площадь плоской фигуры, ограниченной линиями:
а) y = x2 , y = 4 ;		б) y = x2 , y = 2x + 3;
в) y = −x2 + 9, y = x + 7 ;		г) y = ex , y = e−x , x =1;
д) y = x, y = 1 ,	x = 2 ;	е) y = x2 ,	y = x .
x

8.3.7. Найти объем тела, полученного от вращения вокруг оси Ox криволинейной трапеции D , ограниченной линиями:

а) y = x2 , y = 0, x =3;	б) y = e2x , y = 0, x =1, x = 2 ;
в) y = 2x − x2 , y = 0 ;	г) y =sin x,	y = 0,	0 ≤ x ≤ π;
д) xy = 2, y = 0, x =1, x = 3;	е) y = x, y =	1 ,	y = 0, x = 3.
		x

8.3.8. Найти объем тела, полученного от вращения вокруг оси Ox плоской фигуры D , ограниченной линиями:

а)	y = x2 ,	y = x + 2 ;	б) y = x2 +1, y =3x −1;
в)	y = x2 ,	y =8 − x2 ;	г) y2 = 4x, x =1.
			46

8.3.9. Вычислить несобственные интегралы с бесконечным верхним пределом интегрирования и установить их сходимость или расходимость:

∞

а) ∫dx2 ;

б) ∫

;

в) ∫

;

+ x

x +1

∞

д) ∫

;

г) ∫

;

е) ∫

(

)

1 + 3x

x −

xln x

8.3.10. Вычислить несобственные интегралы:

∞

∞ arctg xdx

∞

а) ∫x2e−x

dx ;

б) ∫

;

в) ∫

;

г) ∫

+ x

xln

8.3.11. Исследовать на сходимость интегралы:

∞

а) ∫dxk ;

б) ∫

x(ln x)

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в папке МатАн_ЛинАлг_080100

#
26.02.2016494.69 Кб56Лекции_Математика_2_Дифференциальное исчисление.pdf
#
26.02.2016573.11 Кб53Лекции_Математика_3_Интегральное исчисление.pdf
#
26.02.20161.52 Mб65МА_экз_1курс_экономика_заочн.doc
#
26.02.2016855.38 Кб49Математика_Словарь терминов.pdf
#
26.02.2016630.28 Кб52ПланыПЗ_ЛА_080100.pdf
#
26.02.2016496.78 Кб61ПланыПЗ_МА_080100.pdf