
- •ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
- •080100.62 Экономика
- •Раздел. I. ПРЕДЕЛ ФУНКЦИИ
- •Тема 1. Элементы теории множеств. Понятие функции
- •1.1. Типовые примеры
- •1.2. Контрольные вопросы
- •1.3. Практические задания
- •Тема 2. Теория пределов
- •2.1. Типовые примеры
- •2.2. Контрольные вопросы
- •2.3. Практические задания
- •Тема 3. Предел и непрерывность функции
- •3.1. Типовые примеры
- •3.2. Контрольные вопросы
- •3.3. Практические задания
- •Раздел. II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- •Тема 4. Вычисление производных
- •4.2. Контрольные вопросы
- •4.3. Практические задания
- •Тема 5. Исследование функций на экстремумы и интервалы монотонности
- •5.2. Контрольные вопросы
- •5.3. Практические задания
- •Тема 6. Исследование функций двух переменных
- •6.1. Типовые примеры
- •6.2. Контрольные вопросы
- •6.3. Практические задания
- •Раздел. III. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
- •Тема 7. Решение задач на нахождение неопределенных интегралов. Нахождение неопределенных интегралов различными методами
- •7.2. Контрольные вопросы
- •7.3. Практические задания
- •Тема 8. Вычисление определенных интегралов. Приложения определенного интеграла. Исследование сходимости несобственных интегралов
- •8.1. Типовые примеры
- •8.2. Контрольные вопросы
- •8.3. Практические задания
- •РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
РАЗДЕЛ. I. ПРЕДЕЛ ФУНКЦИИ |
|
|||||
Тема 1. Элементы теории множеств. Понятие функции |
||||||
1.1. Типовые примеры |
|
|
|
|
|
|
Пример 1.1.1. Для функции f (x)= |
x |
|
, x [2,∞) найти |
|||
x2 +1 |
||||||
|
|
|
|
|||
f (−3), f (2), f (4), f (x2 ), f (x +1), |
1 |
. |
||||
f (x) |
||||||
|
|
|
|
|
||
Решение:
Значение функции f (−3)
ласти определения функции.
f (2)= |
2 |
= |
2 |
; f (4)= |
|
22 +1 |
5 |
||||
|
|
|
не вычисляем, т.к. x = −3 не принадлежит об-
|
4 |
= |
|
4 |
; f (x2 )= |
x2 |
|
= |
|
x2 |
; |
4 |
2 |
17 |
2 |
x |
4 |
||||||
+1 |
|
|
(x2 ) +1 |
|
+1 |
|
|||||
f (x +1)= |
x +1 |
|
= |
x +1 |
; |
1 |
= |
x2 +1 |
. |
|
|
|
(x +1)2 |
|
x2 + 2x + 2 |
f (x) |
|
|
|
|
|||||
|
+1 |
|
|
x |
|
|
|
|||||
Пример 1.1.2. Найти область определения функции y = |
x3 |
|||||||||||
|
|
. |
||||||||||
x2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
− 4 |
||
Решение. Функция представлена в виде дроби, которая определена при всех значениях x , для которых определены числитель и знаменатель, и знаменатель не обращается в нуль. Области определения не принадлежат значения x , для которых
x2 − 4 = 0 x2 − 4 = (x + 2)(x − 2) x = −2, x = 2 . |
||||
|
|
|
1 |
2 |
−2 |
2 |
x |
D =(−∞, − 2) (−2,2) (2,∞). |
|
РИС. 1.1.1 |
|
|
|
|
Пример 1.1.3. Найти |
область |
определения, область |
значений функции |
|
y = x −1 и найти значения функции в точках: x1 =1, x2 =5, |
x3 = 0. |
|||
|
|
|
4 |
|
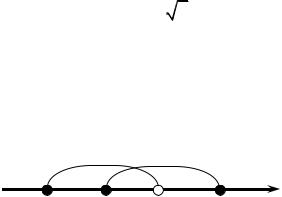
Решение. Область определения D находится из условия x −1 ≥ 0 x ≥1.
Следовательно, D =[1, ∞). |
Область значений E =[0, |
∞) |
(корень арифмети- |
ческий). Частные значения: |
f (1) = 0, f (5)= 4 = 2, |
f (0) |
– не существует. |
Пример 1.1.4. Даны два числовых множества: |
A =[−23,9) и B =[1,17]. |
||
Найти A∩B, A Β, A\B, B\A. |
|
|
|
Решение. Изобразим заданные множества на числовой оси (рис. 1.1.2).
|
A |
B |
|
–23 |
1 |
9 |
17 |
|
РИС. 1.1.2 |
|
|
Тогда решением задачи будут множества |
|
|
|
A ∩ B =[1,9) , A B =[−23,17] , |
A \ B =[−23,1) , B \ A =[9,17]. |
||
1.2.Контрольные вопросы
1)Что называется функцией, областью определения функции, областью значений функции?
2)Какие функции называются основными элементарными функциями?
3)Дайте определение следующих свойств функции: четность, нечетность; периодичность, ограниченность, приведите примеры.
4)Что называется графиком функции?
5)Что называется пересечением множеств?
6)Что называется объединением множеств?
7)Что называется разностью множеств?
1.3.Практические задания
1.3.1. Для функции f (x)= |
x |
|
|
, |
x [2, ∞) найти |
|
|
|
||||
|
|
|
|
|
|
|||||||
|
x2 +1 |
|
|
|
|
|
|
|
||||
f (−3), f (2), |
f (4), |
f (x2 ), |
f (x +1), |
|
1 |
. |
||||||
f |
(x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
1.3.2. Для функции f (x)=1 + 2 |
1 |
|
|
x (0, ∞) найти |
|
|
|
|||||
x |
, |
|
|
|
||||||||
f (0), |
f (1), |
f ( |
5), f |
1 |
, f (a −1). |
|
|
|||||
|
|
|
||||||||||
|
|
|
|
|
|
x2 |
|
|
|
|
||
Построить график функции и вычислить частные значения.
5
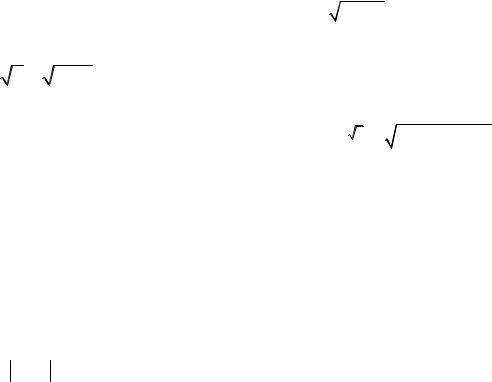
|
3 + x |
при |
x ≤ 0, |
|
|
|
|||
1.3.3. Пусть |
|
|
|
|
|
Найти f (−3), |
f (0), f (1), |
f (4). |
|
f (x)= |
|
|
при |
|
|||||
|
2x |
|
x > 0. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
при |
x < 0, |
|
|
|
||
1.3.4. Пусть |
f (x)= |
|
|
|
|
в точках |
|||
x |
|
|
Найти значения функции |
||||||
|
|
|
2 |
при |
x ≥ 0. |
|
|
|
|
|
|
x |
|
|
|
|
|||
x1 = −2, x2 = 0, x3 =3. |
|
|
|
|
|
|
|||
|
|
0 |
|
при |
x < −1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3.5. Пусть |
f (x)= x +1 |
при |
−1 ≤ x ≤ 0, |
Найти |
|
|
|||
|
1 − x |
при |
0 < x ≤1, |
|
|
|
|||
|
|
0 |
|
при |
x >1. |
|
|
|
|
|
|
|
|
|
|
||||
|
f (−3), f (−1), |
f (0), |
f 1 , |
f (2). |
|
||||
|
|
|
|
|
|
|
2 |
|
|
Найти область определения функций:
1.3.6. y = |
|
x3 |
|
|
||
x2 − 4 |
|
|
||||
|
|
|
||||
1.3.8. y = |
x + |
2 − x |
||||
1.3.10. y = |
1 |
|
+ lg(5x +1) |
|||
x −1 |
||||||
|
|
|
|
|||
1.3.12. y = |
ln x |
|
|
|||
x2 −9 |
||||||
|
|
|||||
Построить графики функций:
1.3.14. y = x2 −1 1.3.16. y = 2x−3
1.3.18. y = cos x
1.3.7. y = |
3x −1 |
|
|
|
|
|
||||
1.3.9. y = |
|
x2 |
|
|
+ |
|
2 |
|
||
x2 + |
|
|
x +1 |
|||||||
|
1 |
|
||||||||
1.3.11. y = 2 x |
+ |
|
|
−x2 − 2x + 3 |
||||||
1.3.13. y = |
1 + |
|
|
|
1 |
|
|
|
||
|
x2 −1 |
|||||||||
|
|
x |
|
|||||||
1.3.15. y = −x3
1.3.17. y = log4 (x + 2)
1.3.19.y =3sin x + π
3
6
