Курсовая работа по курсу «Модулярная арифметика»

Студент Фадеев М.А.

Группа А-06-08

Преподаватель Набебин А.А.

Москва 2010

Задача №23.21

. Зашифровать и расшифровать сообщение с помощью криптосистемы RSA (R. Rivest, A. Shamir, L. Adleman). Простые числа p и q определяются вариантом задания. В качестве исходного текста взять три первых латинских буквы своей фамилии.

p = 5879, q = 5503.

Решение.

Вычисление ключей. Каждый адресат вычисляет свой открытый ключ и ему соответствующий секретный ключ. Адресат должен выполнить следующее:

1. Выбрать два больших различных простых числа p и q примерно одного размера.

2. Найти n = pq и функцию Эйлера φ = φ(n) = (p - 1)(q - 1).

3. Взять случайное число e, 1<e< φ такое, что нод(e, φ) = 1.

4. Найти такое целое a (1, φ), что ea ≡ 1 (mod φ). Для этого с помощью расширенного алгоритма Евклида найти такие целые a, x, что ea + φx = 1. Тогда ea ≡ 1 (mod φ). Пусть произвольное k Z. Сложив ea ≡ 1 (mod φ) и ekφ ≡ 0 (mod φ), получим e(a + kφ) ≡ 1 (mod φ). Если a 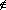(1,φ), то найти такое целое k, что a + kφ (1, φ), и в качестве a взять a + kφ.

5. Открытый ключ адресата есть пара чисел (n,e). Секретный ключ адресата есть число a.

Шифрование. Адресат A шифрует свой текст t и отправляет его адресату B. B дешифрует сообщение от A и получает исходный текст t. Адресат A должен выполнить следующее:

1. Получить открытый ключ (n,e) адресата B.

2. С помощью какого-либо метода M, который публикуется, представить своё письмо t как сообщение в виде натурального числа m из сегмента [0, n-1].

3. Вычислить шифротекст c = m^e (mod n).

4. Отправить свой шифротекст c адресату B.

Дешифрование. Чтобы извлечь текст t из шифротекста c, адресат B должен выполнить следующее:

1. Взять свой секретный ключ a и вычислить сообщение m = c^a (mod n).

2. Вычислить текст t адресата A с помощью метода M.

Адресат A пишет письмо t = SAM адресату B.

Вычисление ключей. Адресат B выполняет следующее:

1. Выбирает два разных простых числа p = 5879, q = 5503.

2. Вычисляет n = pq = 32358581 и функцию Эйлера φ = (p - 1)(q - 1) = 32347200.

3. Выбирает случайное число e = 402631 (1, φ) с нод(e, φ) = 1.

4. С помощью расширенного алгоритма Евклида находит такое a = 7209271 (1, φ), что ea ≡ 1 (mod φ).

5. Открытый ключ адресата B есть пара чисел (n = 32358581, e = 402631). Секретный ключ адресата B есть число a = 7209271.

Шифрование. Адресат А выполняет следующее:

1. Получает открытый ключ (n = 32358581, e = 402631) адресата B.

2. Представляет свой текст t = FAD в виде натурального числа m из [0, n-1] с помощью 27-ричной системы счисления следующим образом. Нумеруются буквы алфавита:

пробел	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20

U	V	W	X	Y	Z
21	22	23	24	25	26

Текст FAD представляется в виде числа m = 6 * 27² + 1 * 27 + 4 = 14610

3. Шифрует своё сообщение m = 13891 числом c = m^e (mod n) =14610⁴⁰²⁶³¹ (mod 32358581) = 16028906.

4. Посылает свой шифротекст c адресату B.

Дешифрование. Чтобы дешифровать шифротекст c от A, адресат B выполняет следующее:

1. Находит (с помощью своего секретного ключа a) число m = c^a (mod n) = 16028906^7209271 (mod 32358581) = 14610.

2. Представляет число m в 27-ричной системе счисления: m = (19 1 13)₂₇ и получает исходный текст FAD.

Замечание. Криптографическая стойкость криптосистемы RSA основана на трудной практической осуществимости проблемы факторизации больших чисел. На практике для криптографической стойкости модуль n задаётся двоичным числом с 1024 и более двоичными разрядами.

Текст t в компьютере представляется бинарным массивом, который рассматривается как бинарная запись некоторого числа m. Предложенный выше способ представления текста числом носит иллюстративный характер и выбран из желания оперировать небольшими числами.

Задача 24.21

Зашифровать и расшифровать сообщение с помощью криптосистемы RSA (R. Rivest, A. Shamir, L. Adleman). Простые числа p и q взять из задачи 29. В качестве исходного текста взять три первых латинских буквы своей фамилии.

p = 490663, q = 27259, t = FAD.

Вычисление ключей. Каждый адресат создает открытый ключ и ему соответствующий секретный ключ. Адресат должен выполнить следующее.

1. Выбрать два больших различных случайных простых числа p и q примерно одного размера.

2. Найти n = p ∙ q и функцию Эйлера φ = φ(n) = (p − 1)(q − 1).

3. Взять случайное число e, 1 < e < φ, такое, что нод(e, φ) = 1.

4. Найти такое целое a (1,φ), что ea ≡ 1 (mod φ). С помощью расширенного алгоритма Евклида найти то единственное целое a, 1 < d < φ, для которого ea ≡ 1 (mod φ).

5. Открытый ключ адресата есть пара чисел (n, e). Секретный ключ адресата есть число a.

Вычисление подписи. Адресат А подписывает свой текст t. Любой адресат B может проверить подпись A и извлечь из нее текст t. Адресат A должен выполнить следующее.

1. Каким – либо методом M (который публикуется) представить свой текст t в виде целого числа m, 1 < m < n – 1.

2. Найти число w = R(m) с помощью открытой функции

R : [0, n – 1] → M_R , где M_R есть некоторое числовое множество, например,

R(m) = m*m, где a*b есть результат приписывания слова b к слову a. Тогда M_R = {w = m*m: m [0, n – 1]}.

3. Найти число s = w ^a(mod n).

4. Отправить подписанный шифротекст s адресату В.

Проверка подписи и вычисление сообщения. Чтобы проверить подпись s адресата A и извлечь из нее сообщение m, адресат B должен выполнить следующее.

1. Получить открытый ключ (n, e) адресата A.

2. Найти число w = s ^e(mod n).

3. Проверить, что w M_R . Если нет, отвергнуть подпись s.

4. Найти число m = R^–1(w).

5. С помощью метода M найти отправленный текст t.

Решение:

Адресат A подписывает свой текст t. Любой адресат B может проверить подпись A.

Вычисление ключей. Адресат А выполняет следующее.

1. Выбирает разные простые числа p = 490663 и q = 27259.

2. Находим n = p ∙ q = 490663 * 27259 = 13374982717 и функцию Эйлера

φ = φ(n) = (p − 1)(q − 1) = 490662 * 27258 = 13374464796.

3. Выбирает случайное число e = 405577, 1 < e < φ, с нод(e, φ) = 1.

4. С помощью расширенного алгоритма Евклида находит то единственное целое a = 4233244969(1,φ), которое удовлетворяет сравнению

ea ≡ 1 (mod φ), это сравнение 405577d ≡ 1 (mod 13374464796).

6. Открытый ключ для А есть пара (n = 13374982717, e = 405577).

7. Секретный ключ для А есть число a = 4233244969.

Вычисление подписи. Адресат А подписывает свой текст t = FAD и выполняет следующее.

1. Представим свой текст t = FAD числом каким – либо методом M, например, в 27 – ричной системе счисления числом

m = 6 * 27² + 1 * 27 + 4 = 14079.

Нумеруются буквы алфавита:

пробел	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18

S	T	U	V	W	X	Y	Z
19	20	21	22	23	24	25	26

2. Вычисляет w = R(m) = R(14079) = 14079*14079 = 1407914079.

3. Вычисляет подпись

s = w ^a(mod n) = 1407914079^4233244969 (mod 13374982717) = 16252024181622.

4. Отправляет подписанный шифротекст s адресату В.

Проверка подписи и вычисление сообщения. Адресат B получает от A подписанный шифротекст s и делает следующее.

1. Получить открытый ключ (n = 13374982717, e = 405577) адресата A.

2. С помощью открытого ключа (n, e) адресата А вычисляет:

w = s ^e(mod n) = 16252024181622⁴⁰⁵⁵⁷⁷ (mod 13374982717) = 1407914079.

3. Так как w = 1407914079 = 14079*14079 и M_R , то B принимает

подпись А.

4. Вычисляет m = R^–1(w) = 14079.

5. Представляет число m = (14079)₁₀ в 27 – ричной системе счисления

m = (6 1 4)₂₇ и получает исходный текст t = FAD.

Замечание. Допустима цифровая подпись RSA,основанная на использовании криптографической хэш – функции h: {0, 1}* → _n, где n есть число элементов в мультипликативной группе G. Предполагается, что каждый элемент r из G может быть представлен в бинарной записи f(r) с тем, чтобы можно было вычислить значение хэш – функции h(f(r)).

Алгоритм вычисления значений хэш – функции публикуется.

Заметим, что содержимое любого файла есть некоторый текст t, представляемый в компьютере как последовательность нулей и единиц, которая есть некоторое бинарное слово m (в алфавите {0, 1}), являющееся битовым набором m, составленным из кодов ASCII для последовательных символов текста t. Хэш – функция h сопоставляет бинарному набору m уникальный бинарный набор фиксированной длины (на практике это набор длины 128, 160 или 256 бит, в зависимости от выбранной хэш – функции), который может рассматриваться как двоичное число (в системе счисления по основанию 2) и которое затем, вообще говоря, можно представить числом в системе счисления по любому основанию h. В конечном итоге с помощью хэш – функции тексту t ставится в соответствие уникальное число в системе счисления по любому нужному основанию.

Значение хэш – функции есть большое число, выходящее за пределы величин целых чисел, допустимых в алгоритмических языках программирования. MatCad, например, допускает целые (10 – ричные) числа длины не более 18 цифр. Для работы с большими целыми числами с длиной десятеричной записи в 100 и более цифр приходится писать специальный программный процессор. Поэтому в последующих примерах значение хэш – функции записывается искусственно, для примера, небольшим числом.

Вычисление ключей. Пусть по-прежнему: пара (n = 13374982717, e = 405577) есть открытый ключ для А и число a = 4233244969 есть секретный ключ для A.

Вычисление подписи. Адресат А подписывает свой текст t произвольной длины. Любой адресат B может проверить подпись A под его текстом t. Адресат A должен выполнить следующее.

1. Вычислить значение хэш – функции h = h(t). Пусть для примера текст

t = FAD, m = 6 * 27² + 1 * 27 + 4 = 14079, h = h(m) = m = 14079.

2. Вычислить s = h ^a (mod n) = 14079^4233244969 (mod 13374982717). Число s есть подпись A под его текстом t.

Проверка подписи и вычисление сообщения. Чтобы проверить подпись s адресата A, адресат B должен выполнить следующее.

1. Получить открытый ключ (n = 13374982717, e = 405577) адресата A.

2. Вычислить значение хэш – функции h = h(t). Если текст t не изменялся, то h = 14079.

3. Вычислить h1 = s ^e(mod n) = 16252024181622⁴⁰⁵⁵⁷⁷ (mod 13374982717) = = 14079.

4. Принять подпись, если h = h1, и отвергнуть в противном случае. Так как h = h1 = 14079, то подпись принимается.

Задача 25.21

Зашифровать и расшифровать сообщение с помощью криптосистемы ЭльГамаля. В качестве простого числа p взять большее число варианта из задачи 29. В качестве исходного текста взять три первые латинские буквы совей фамилии.

p = 490663, t = FAD

Вычисление ключей. Каждый адресат создает свой открытый ключ и ему соответствующий секретный ключ. Адресат должен выполнить следующее.

1. Выбрать случайное простое число p и найти генератор α мультипликативной группы ^*_р целых чисел по модулю p, используя алгоритм Гаусса.

2. Выбрать случайное число a [1, p – 2] и найти y = α^a (mod p).

3. Открытый ключ адресата есть тройка чисел (p, α, y). Секретный ключ адресата есть число a.

Шифрование. Адресат А шифрует свой текст t и отправляет шифротекст адресату В. В дешифрует сообщение от А и получает исходный текст t. Адресат А должен выполнить следующее.

1. Получить открытый ключ (p, α, y) адресата В.

2. С помощью какого – либо метода М, который публикуется, представить свое письмо t как сообщение в виде натурального числа m из сегмента [0,p–1]

3. Выбрать случайное число k, 1 ≤ k ≤ p – 2.

4. Вычислить γ = α^k (mod p) и δ = m · y^k (mod p).

5. Отправить свой шифротекст c = (γ, δ) адресату В.

Дешифрование. Чтобы получить исходный текст t по c = (γ, δ), адресат В должен выполнить следующее.

8. Взять свой секретный ключ a и вычислить целое число γ ^{p – 1 – a} (mod p).

9. Вычислить m = (γ ^{– a} · δ)(mod p), где γ ^{– a} = (γ ^{– 1} )^а , а число γ ^{– 1} есть решение сравнения х · γ ≡ 1(mod p) и вычисляется с помощью расширенного алгоритма Евклида.

10. Вычислить исходный текст t от А с помощью метода M.

Решение:

Адресат А пишет письмо t = FAD адресату В.

Вычисление ключей. Адресат В выполняет следующее.

1. Выбирает простое число p = 490663 и находит генератор α = 3 для мультипликативной группы 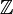^*₄₉₀₆₆₃ .

2. Выбирает случайное число а = 405577 1 ≤ а ≤ р – 2, и вычисляет

y = α^a (mod p) = 3⁴⁰⁵⁵⁷⁷ (mod 490663) = 188403.

3. Открытый ключ адресата В есть тройка (р = 490663, α = 3, у = 188403). Секретный ключ адресата В есть число а = 405577.

Шифрование. Адресат А шифрует свой текст t = FAD и выполняет следующее.

1. Получает открытый ключ (р = 490663, α = 3, у = 188403) для В.

2. Представляет свой текст t = FAD в виде натурального числа m из

[0, p – 1], с помощью какого – либо метода, например, с помощью 27 – ричной системы счисления числом m = 6*27² + 1*27 + 4 = 14079.

3. Выбирает случайное число k = 1751, 1 ≤ k ≤ р – 2.

4. Вычисляет γ = α^k (mod p) = 3¹⁷⁵¹ (mod 490663) = 208275,

δ = m · y^k (mod p) = 14079 · 188403¹⁷⁵¹ (mod 490663) = 87345.

5. Посылает шифротекст с = (γ = 208275, δ = 6008227329) адресату В.

Дешифрование. Чтобы дешифровать шифротекст c = (γ = 208275, δ = 87345) от А, адресат В выполняет следующее.

1. Вычисляет

γ ^{p – 1 – a} (mod p) = 208275⁸⁵⁰⁸⁵ (mod 490663) = 62974.

m = (γ ^{p -1 - a} · δ)(mod p) = ((γ ^{p -1 - a})(mod p) · δ)(mod p) =

(208275⁸⁵⁰⁸⁵ (mod 490663) ∙ 87345)(mod 490663) = 131800.

2. Представляет число m 27– ричной системе счисления: m = (6 1 4)₂₇ и получает исходный текст FAD.

Замечание. Криптографическая стойкость криптосистемы ЭльГамаля основана на трудной практической осуществимости проблемы нахождения дискретного логарифма в группе ^*_р при больших простых числах р. На практике для криптографической стойкости простое число р задается двоичным числом с 1024 и более двоичными разрядами.

Программный код:

См. Приложение.

Вычисление ключей.

1.

_2.

_3. (р = 490663, α = 3, у = 188403)

Шифрование.

1. (р = 490663, α = 3, у = 188403)

2. t := FAD

_3.

4.

_{5. c = (γ = 208275, δ = 87345)}

Дешифрование.

1.

_2.

m = (6 1 4)

Задача 26.21

Вычислить и проверить подпись под сообщением с помощью криптосистемы ElGamal для электронной подписи. В качестве простого числа р взять большое число из задачи 23. В качестве исходного текста взять слова своего полного имени: фамилия, имя, отчество.

p = 5897 t = FMA

При использовании схемы цифровой подписи ЭльГамаля по тексту письма t вычисляется значение хэш – функции h(t), которое затем используется при вычислении и проверке цифровой подписи под текстом сообщения.

Вычисление ключей. Каждый адресат создает открытый ключ и ему соответствующий секретный ключ. Далее адресат должен выполнить следующее.

1. Выбрать случайное простое число p и найти генератор α мультипликативной группы ^*_р .

2. Выбрать произвольное число a, 1 ≤ a ≤ р – 1.

3. Вычислить y = α^a (mod p).

4. Открытый ключ адресата есть тройка чисел (p, α, y). Секретный ключ адресата есть число a.

Вычисление подписи. Адресат А подписывает свой текст t (произвольной длины). Любой адресат B может проверить подпись адресата A под его текстом t. Адресат A должен выполнить следующее.

3. Вычислить значение хэш – функции h(t).

2. Выбрать случайное секретное целое число k из [1, p – 2] такое, что нод(k, p – 1) = 1.

3. Вычислить k ^{– 1} (mod (p – 1)).

4. Вычислить r = α^k (mod p).

5. Вычислить s = k ^{– 1} (h(t) – ar) (mod (p – 1)).

6. Подпись адресата А под его текстом t есть пара (r, s).

Проверка подписи. Чтобы проверить подпись (r, s) адресата A под его текстом t, адресат B должен выполнить следующее.

11. Вычислить значение хэш – функции h(t).

12. Получить открытый ключ (p, α, y) адресата А.

13. Проверить, что r [1, p – 1]; если нет, отвергнуть подпись.

14. Вычислить v₁ = y^r r^s (mod p).

15. Вычислить v₂ = α^h(m)(mod p).

16. Принять подпись, если v₁ = v₂ и опровергнуть в противном случае.

Решение:

Адресат А подписывает свой текст t. Любой адресат В может проверить подпись А.

Вычисление ключей. Адресат А выполняет следующее.

1. Выбирает простое число p = 5897 и находит генератор α = 3 мультипликативной группы ^*_р целых чисел по модулю р.

2. Выбрать случайное целое a = 1751, 1 ≤ a ≤ р – 1.

3. Вычисляет y = α^a (mod p) = 3¹⁷⁵¹ (mod 5897) = 3818.

4. Открытый ключ адресата A есть тройка чисел (p = 5897, α = 3, y = 3818). Секретный ключ адресата A есть число a = 1751.

Вычисление подписи. Адресат А подписывает свой текст t и для этого выполняет следующее.

1. Вычисляет значение хэш – функции h(t). Пусть для примера h(t) =1550.

2. Выбрать случайное секретное целое число k = 1579 из [1, p – 2] такое, что нод(k, p – 1) = 1.

3. Вычислят k ^{– 1} (mod (p – 1)) = 1579 ^{– 1} (mod 5896) = 1369.

4. Вычисляет r = α^k (mod p) = 3¹⁵⁷⁹ (mod 5897) = 5032.

5. Вычисляет s = k ^{– 1} (h(t) – ar) (mod (p – 1)) =

= 1369 ∙ (1550 – 1751∙ 5032)(mod 5897) = 3825.

6. Подпись адресата А есть пара (r = 5032, s = 3825).

Проверка подписи. Чтобы проверить подпись (r = 5032, s = 3825) адресата A под его текстом t, адресат B должен выполнить следующее.

1. Вычисляет значение хэш – функции h(t). Если текст t не изменялся, то h(t) =1550.

2. Получает открытый ключ (p = 5897, α = 3, y = 3818) адресата А.

3. Проверяет, что r = 5032 [1, p – 1] = [1, 5896].

4. Вычисляет число v₁ = y^r r^s (mod p) = 3818⁵⁰³² ∙ 5032³⁸²⁵ (mod 5897) = 1582.

5. Вычисляет число v₂ = α^h(t)(mod p) = 3¹⁵⁵⁰ (mod 5897) = 1582.

6. Принимает подпись, ибо если v₁ = v₂ .

Для Криптографической стойкости рекомендуется брать р длиной между 512 бит (лучше 768) и 1024 бит включительно.

Код программы:

См. Приложение

Вычисление ключей.

1.

2.

_3.

4. (p = 5897, α = 3, y = 3818)

Вычисление подписи.

_1.

2.

_3.

4.

5.

s = 3825

6. (r = 5032, s = 3825)

Проверка подписи.

_1.

2. (p = 5897, α = 3, y = 3818)

3. r = 5032

4.

v1 = 1582

5.

_{6. v1 = v2}

Задача 27.21

Зашифровать и расшифровать сообщение с помощью (обобщенной) криптосистемы ЭльГамаля над (конечным) полем Галуа GF(p^m). Взять простое число р = 31, натуральное m = 3. Неприводимый полином над _р определяется номером варианта. В качестве исходного текста взять три первые латинские буквы своей фамилии.

23х³ + 6, р = 31, m = 3, t = FAD.

Решение:

Числовая схема шифрования ЭльГамаля может быть обобщена для работы в любой конечной циклической группе G . Криптографическая стойкость схемы ЭльГамеля в группе G основана на трудности решения проблемы дискретного логарифма в G. Группа G должна удовлетворять следующим условиям.

1. Эффективность, то есть групповые операции в G должны вычисляться относительно просто.

2. криптографическая стойкость, то есть решение проблемы дискретного логарифма в Gдолжно быть практически неосуществимой.

Ниже следуют удовлетворяющие этим двум условиям группы, из которых первые три наиболее употребительны.

1. Мультипликативная группа ^*_р целых чисел по модулю простого числа р.

2. Мультипликативная группа ^*₂^s конечного поля ₂^s характеристики два.

3. Группа точек эллиптической кривой над конечным полем.

4. Мультипликативная группа ^*_q конечного поля |F_q , где q = p ^s , р есть простое число, s есть положительное простое число.

5. Группа обратимых элементов ^*_n , где n есть составное целое число.

6. Якобиан гиперэллиптической кривой над конечным полем.

7. Класс групп мнимого квадратичного числового поля (imaginary quadratic number field).

Адресат А шифрует свой текст t и отсылает шифротекст адресату В. В дешифрует сообщение от А и получает исходный текст t.

Вычисление ключей. Каждый адресат создает свой открытый ключ и ему соответствующий секретный ключ. Далее адресат должен выполнить следующее.

1. Выбрать подходящую (мультипликативную) циклическую группу G порядка n.

2. Найти генератор α группы G.

3. Выбрать случайное целое число a, 1 ≤ a ≤ n – 1.

4. Вычислить элемент y = α^a группы G.

5. Открытый ключ адресата есть пара чисел (α, y) элементов группы G. Открыто также описание умножения элементов в G. Секретный ключ адресата есть число a.

Шифрование. Адресат А шифрует свой текст t и отправляет шифротекст адресату В. Адресат А должен выполнить следующее.

1. С помощью какого – либо метода М, который публикуется, представить свое письмо t как элемент m группы G.

2. Получить открытый ключ (α, y) адресата В.

3. Выбрать случайное целое число k, 1 ≤ k ≤ n – 1.

4. Вычислить γ = α^k и δ = m · y^k .

5. Отправить свой шифротекст c = (γ, δ) адресату В.

Дешифрование. Чтобы получить исходный текст t по c = (γ, δ), адресат В должен выполнить следующее.

17. Взять свой секретный ключ a и вычислить целое число γ ^{– a} и найти γ ^{– a} = (γ ^a ) ^{– 1}.

18. Вычислить m = (γ ^{– a} · δ).

19. Вычислить исходный текст t от А с помощью метода M.

Замечание. Все адресаты могут выбрать одну и ту же циклическую группу G и ее генератор α.

Криптосистема ЭльГамаля с мультипликативной группой конечного поля |F_p^m , р = 35, m = 3. Пусть для удобства элемент поля а₂ х² + а₁ х + а₀ представляется р – ричной стрингом (а₂ а₁ а₀).

Адресат А подписывает свой текст t = FAD и отправляет шифротекст адресату В. В дешифрует сообщение от А и получает исходный текст t.

Вычисление ключей. Адресат В выполняет следующее.

1. Выбирает мультипликативную группу G конечного поля (Е³₃₅ , {+, ∙}), элементы которого представляются полиномами из ₃₅ [х] над ₃₅ степени меньше 3 и умножение в котором выполняется по модулю неприводимого полинома f(x) = (23 0 0 6) = 23х³ + 6 из ₃₅ [х]. Группа G имеет порядок

n = p^m – 1 = 35³ – 1 = 42874.

2. Находит генератор α = х + 5 = (0 1 5) группы G.

3. Выбрать случайное целое число a = 2, 1 ≤ a ≤ n – 1.

4. Вычислить элемент y = α^a (mod f(x)) = (х + 5)² (mod f(x)) = х² + 10х + 25 = (1 10 25) группы G.

5. Открытый ключ адресата для В есть пара чисел (α = (0 1 5),

y = (1 10 25)) вместе с полиномом f(x), который определяет умножение в G, если f(x) и α не есть параметры, общие всем адресатам. Секретный ключ для В есть число a = 2.

Шифрование. Адресат А шифрует свой текст t и отправляет шифротекст адресату В. Адресат А должен выполнить следующее.

1. Представляет свой текст t = FAD как элемент m1 группы G. Чтобы зашифровать письмо t, адресат А кодирует текст t каким – либо способом, например, в 27 – ричной системе счисления 10 – ричным числом

u = 6 * 27² + 1 * 27 + 4 = 14079₁₀ , а затем вычисляет 35 – ричное представление числа u в виде сообщения m1 = (6 1 4)₃₅ , рассматриваемом как полином 6х² + 1х + 4 из ₃₅ [х].

2. Получить открытый ключ (α = (0 1 5), y = (1 10 25)) адресата В.

3. Выбрать случайное целое число k = 1575, 1 ≤ k ≤ n – 1.

4. Вычислить γ = α^k = (х + 5)¹⁵⁷⁵ (mod f(x)) = 5х² + 25х + 23 = (5 25 23),

y^k = (х² + 10х + 25)¹⁵⁷⁵ (mod f(x)) = 15х² + 25х + 24=(15 25 24) δ = m1 · y^k = (11 17 9) · (15 25 24) = (11х² + 17х + 9) ∙ (15х² + 25х + 24)

(mod f(x)) = 19х² + 33х + 26 = (19 33 26).

5. Отправить свой шифротекст c = (γ =(5 25 23), δ =(19 33 26)) адресату В.

Дешифрование. Чтобы получить исходный текст t по c = (γ, δ), адресат В должен выполнить следующее.

1. Пользуясь своим секретным ключом a, адресат В вычисляет следующие элементы группы

γ ^a = (5 25 23)² = (5х² + 25х + 23)² (mod f(x)) = 15х² + 25х + 24 = (15 25 24),

γ ^{– a} = (γ ^a ) ^{– 1} = (15 25 24)^{– 1} = (15х² + 25х + 24) ^{– 1} (mod f(x)) = (7 6 11) .

2. Вычислить m1 = (γ ^{– a} · δ) = (7 6 11) ∙ (19 33 26) (mod f(x)) =

= (7х² + 6х + 11) ∙ (19х² + 33х + 26) (mod f(x)) = 11х² + 17х + 9 = (11 17 9).

3. Чтобы получить текст t по элементу m, адресат В производит следующие вычисления.

m1 = (11 17 9)₃₅ = 11*35² + 17*32 + 9 = 14079₁₀ = (19 8 12)₂₇ , откуда текст

t = FAD.

Программный код:

См. Приложение

Вычисление ключей.

1. f(x) := (23 0 0 6)

2.

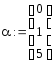
3. a := 2

4.

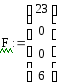
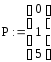
5. (α = (0 1 5), y = (1 10 25))

Шифрование.

1.

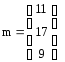
_2. (α = (0 1 5), y = (1 10 25))

3.

4.

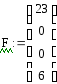
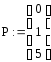
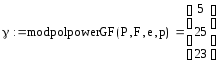
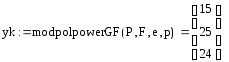
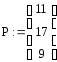
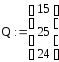
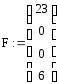
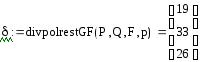
5. c = (γ = (5 25 23), δ = (19 33 26))

Дешифрование.

1.

₌

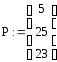
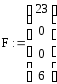
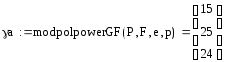
2.

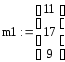
3.

Задача 28.21.

Вычислить и проверить подпись под сообщением с помощью (обобщенной) криптосистемы ЭльГамаля для электронной подписи над (конечным) полем Галуа GF(p^m). Взять простое число р = 31, натуральное

m = 3. Неприводимый полином над _р взять из задачи 27. В качестве исходного текста взять слова своего полного имени: фамилия, имя, отчество.

23х³ + 6, р = 31, m = 3, t = FMA.

Решение:

Схема электронной цифровой подписи ЭльГамаля, основанная на мультипликативной группе ^*_р , может быть обобщена на любую конечную абелеву группу G. Алгоритм подписи использует криптографическую хэш – функцию h: {0, 1}*→ _n , где n есть число элементов в G. Предполагается, что каждый элемент r из G может быть представлен в бинарной записи f(r) c тем, чтобы можно было вычислить значение хэш – функции h(f(r)).

Алгоритм вычисления хэш – функции публикуется.

Криптографическая стойкость подписи основана на трудной осуществимости проблемы нахождения дискретного логарифма в группе G большого порядка.

При использовании схемы цифровой подписи ЭльГамаля по тексту письма t вычисляется значение хэш – функции h(t), которое затем используется при вычислении и проверке цифровой подписи под текстом письма.

Вычисление ключей. Каждый адресат создает свой открытый ключ и ему соответствующий секретный ключ. Далее адресат должен выполнить следующее.

1. Выбрать подходящую (мультипликативную) циклическую группу G порядка n.

2. Найти генератор α группы G.

3. Выбрать случайное целое число a, 1 ≤ a ≤ n – 1.

4. Вычислить элемент y = α^a группы G.

5. Открытый ключ адресата есть пара чисел (α, y) элементов группы G. Открыто также описание умножения элементов в G. Секретный ключ адресата есть число a.

Вычисление подписи. Адресат А подписывает свой текст t (произвольной длины). Любой адресат B может проверить подпись адресата A под его текстом t. Адресат A должен выполнить следующее.

4. Вычислить значение хэш – функции h(t).

2. Выбрать случайное секретное целое число k из [1, n – 1], для которого нод(k, n) = 1.

3. Вычислить целое число k ^{– 1} (mod (n)).

4. Вычислить элемент r = α^k группы G.

5. Вычислить значение хэш – функции h(r).

6. Вычислить число m = k ^{– 1} (h(t) – ar(r)) (mod (n)).

7. Подпись адресата А под его текстом t есть пара (r, m).

Проверка подписи. Чтобы проверить подпись (r, m) адресата A под его текстом t, адресат B должен выполнить следующее.

20. Вычислить значение хэш – функции h(t).

21. Получить открытый ключ (α, y) для адресата А.

22. Вычислить значение хэш – функции h(r).

23. Вычислить в группе G элементы: v₁ = y^h(r) r^m, v₂ = α^h(t).

24. Принять подпись, если v₁ = v₂ и опровергнуть в противном случае.

Схема электронной (цифровой) подписи ЭльГамаля с мультипликативной группой конечного поля |F_p^m , р = 31, m = 3. Пусть для удобства элемент поля а₂ х² + а₁ х + а₀ представляется р – ричной стрингом (а₂ а₁ а₀).

Адресат А подписывает свой текст t = FMA. Любой адресат В может проверить подпись А.

Вычисление ключей. Адресат А выполняет следующее.

1. Выбирает мультипликативную группу G = ₃₁³ – {0} конечного поля (₃₁³ , {+, ∙}), элементы которого представляются полиномами из ₃₁ [х] над ₃₁ степени меньше 3 и умножение в котором выполняется по модулю неприводимого полинома f(x) = (23 0 0, 6) = 23х³ + 6 из ₃₁ [х]. Группа G имеет порядок n = p^m – 1 = 31³ – 1 = 29790.

2. Находит генератор α = х + 5 = (0 1 5) группы G.

3. Выбрать случайное целое число a = 2, 1 ≤ a ≤ n – 1.

4. Вычислить элемент y = α^a (mod f(x)) = (х + 5)² (mod f(x)) = х² + 10х + 25 = (1 10 25) группы G.

5. Открытый ключ адресата для А есть пара чисел (α = (0 1 5),

y = (1 10 25)) вместе с полиномом f(x), который определяет умножение в G, если f(x) и α не есть параметры, общие всем адресатам). Секретный ключ для А есть число a = 2.

Вычисление подписи. Адресат А подписывает свой текст t. Адресат А выполняет следующее.

2. Вычисляет значение хэш – функции h(t). Пусть для примера h(t) =1550.

2. Выбрать случайное секретное целое число k = 1579 из [1, n – 1], такое, что нод(k, n) = 1.

3. Вычисляет целое число k ^{– 1} (mod (n)) = 1579 ^{– 1} (mod 29790) = 5869.

4. Вычисляет в группе G элемент r = α^k = (0 1 5)¹⁵⁷⁹ = (х + 5)¹⁵⁷⁹ (mod f(x)) = (3 21 18).

5. Вычисляет значение хэш – функции h(r), например, следующим образом. По r = (3 21 18) вычисляет в _n 10-ричное число (3 21 18)₃₁ = 3х² + 21х + 18 = 3*31² + 21*31 + 18 = 3552₁₀. Пусть для примера h(r) = 3552₁₀.

6. Вычисляет в _n число m = k ^{– 1} (h(t) – ah(r)) (mod (n)) = 1579 ^{– 1} · (1550 – - 2*3552) (mod (n)) = 23624.

7. Подпись адресата А под его текстом t есть пара(r=(3 21 18), m=23624₁₀).

Проверка подписи. Чтобы проверить подпись (r, m) адресата A под его текстом t, адресат B выполняет следующее.

1. Вычислить значение хэш – функции h(t). Если текст t не изменялся, то h(t) = 1550₁₀ .

2. Получить открытый ключ (α = (0 1 5), y = (1 10 25)) адресата А.

3. Вычислить значение хэш – функции h(r). Если вектор r не менялся, то h(r) = 3552₁₀.

4. Вычислить в группе G элементы:

v₁ = y^h(r) r^m = (1 10 25)³⁵⁵² ∙ (3 21 18)²³⁶²⁴ =(х² + 10х +25)³⁵⁵² · (3х² + 21х + 18)²³⁶²⁴ (mod (f(x))) = (21 8 12),

v₂ = α^h(t) = (0 1 5)¹⁵⁵⁰ = (x + 5)¹⁵⁵⁰ (mod (f(x))) = (21 8 12).

4. Так как v₁ = v₂ , то В принимает подпись адресата А.

Программный код:

См. Приложение

Вычисление ключей.

1. f(x) = (23 0 0 6)

2.

3.

4.

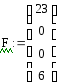
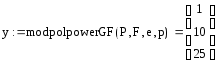
5. α = (0 1 5), y = (1 10 25)

Вычисление подписи.

1. h1 := 1550

2. _{n := 29790}

_{3. = 5869}

4.

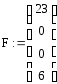
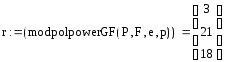
5.

6.

m = 23624

7. r = (3 21 18), m = 23624

Проверка подписи.

1. h1 := 1550

2. (α = (0 1 5), y = (1 10 25))

3. h2 = 3552

4.

₌

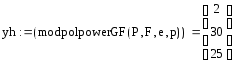
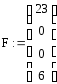
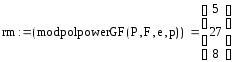
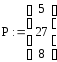
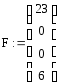
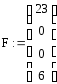
5. v1 = v2

Задача 29.21.

Вычислить и проверить подпись под сообщением с помощью криптосистемы DSA (Digital Signature Algorithm) для электронной подписи. Простые числа p и q определяются вариантом задания. В качестве исходного текста взять слова своего полного имени: фамилия, имя, отчество.

р = 490663, q = 27259, t = FMA

Вычисление ключей. Каждый адресат создает свой открытый ключ и ему соответствующий секретный ключ. Адресат должен выполнить следующее.

1. Выбрать простое число q, 2¹⁵⁹ < q < 2¹⁶⁰ .

2. Выбрать число t, 0 ≤ t ≤ 8, и простое число р, 2^{511 + 64 t} < p < 2^{512 + 64 t} такое, что q делит p – 1.

3. Найти генератор α 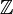^*_р для циклической подгруппы порядка q в группе ^*_р . Для этого адресат должен выполнить следующее.

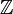   1. Выбрать элемент g ^*_р и найти α = g^{(p – 1)/q} (mod p).

   2. Если α = 1, то перейти к шагу 3.1 с другим g.

4. Выбрать произвольное число а, 1 ≤ а ≤ q – 1.

5. Вычислить y = α ^a (mod p).

6. Открытый ключ адресата есть (p, q, α, y); секретный ключ адресата есть число а.

Вычисление подписи. Адресат А подписывает свой текст t (произвольной длины). Любой адресат В может проверить подпись А под текстом t с помощью открытого ключа адресата А. Адресат А выполняет следующее.

1. Вычисляет значение хэш – функции h(t).

2. Выбрать произвольное секретное число k, 0 < k < q.

3. Вычислить k ^{– 1} (mod q).

4. Вычислить r = (α^k (mod p)) (mod q).

5. Вычислить s = k ^{– 1} (h(t) + ar) (mod q).

6. Подпись адресата А есть пара чисел (r, s).

Проверка подписи. Чтобы проверить подпись (r, s) адресата А под его текстом t, адресат В должен выполнить следующее.

1. Вычислить значение хэш – функции h(t).

2. Взять открытый ключ (p, q, α, y) адресата А.

3. Проверить, что 0 < r < q и 0 < s < q. Если нет, то отвергнуть подпись.

4. Вычислить w = s ^{– 1} (mod q) и h(m).

5. Вычислить u₁ = w · h(m) (mod q) и u₂ = r w (mod q).

6. Вычислить v = (α ^u1 y ^u2 (mod p)) (mod q).

7. Принять подпись, если v = r и отвергнуть в противном случае.

Решение:

Адресат А подписывает свой текст t и всякий адресат В может проверить подпись А.

Вычисление ключей. Адресат должен выполнить следующее.

1. Выбрать простое число q = 27259.

2. Выбрать простое число р = 490663, для которого q делит (p – 1). Пусть (p – 1)/ q = 18.

3. Выбрает случайное число g=2575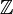^*_р и вычисляет α = g^{(p – 1)/q} (mod p) = = 2575¹⁸ (mod 490663) = 459706. Так как α ≠ 1, то α есть генератор для единственной циклической подгруппы порядка q в группе ^*_р . (Если α = 1, то следует выбрать другое g).

4. Выбрать случайное число а = 75 [1, q – 1].

5. Вычислить y = α ^a (mod p) = 459706⁷⁵ (mod 490663) = 169635.

6. Открытый ключ адресата есть (p = 490663, q = 27259, α = 459706,

y = 169635); секретный ключ адресата А есть число а = 75.

Вычисление подписи. Чтобы подписать свой текст t (произвольной длины), адресат А делает следующее.

1. Вычисляет значение хэш – функции h(t). Пусть для примера h(t) =1557.

2. Выбирает случайное секретное число k = 57[0, q].

3. Вычисляет k ^{– 1} (mod q) = 16738.

4. Вычисляет r = (α^k (mod p)) (mod q) = (459706⁵⁷ (mod 490663))

(mod 27259) = 25077.

5. Вычисляет s = k ^{– 1} ∙ (h(t) + ar) (mod q) = 16738 ∙ (1557 + 75 ∙ 25077)

(mod 27259) = 2895.

6. Подпись адресата А под его текстом t есть пара чисел (r = 25077,

s = 2895).

Проверка подписи. Чтобы проверить подпись (r = 25077, s = 2895)

адресата А под его текстом t, адресат В должен выполнить следующее.

1. Вычисляет значение хэш – функции h(t). Если текст t не изменялся, то

h(t) = 1557.

2. Берет открытый ключ адресата А: (p = 490663, q = 27259, α = 459706,

y = 169635).

3. Проверяет, что r = 25077 [0, q] = [0, 27259] и s = 2895 [0, q] =

= [0, 27259]. Если проверка не проходит, то подпись отвергнут.

4. Вычисляет w = s ^{– 1} (mod q) = 25244.

5. Вычисляет u₁ = w · h(t) (mod q) = 25244 ∙ 1557(mod 27259) = 24689,

u₂ = r w (mod q) = 25077 ∙ 25244(mod 27259) = 8031.

6. Вычисляет v = (α ^u1 y ^u2 (mod p)) (mod q) = (459706²⁴⁶⁸⁹ ∙ 169635⁸⁰³¹

(mod 490663))(mod 27259) = 25077.

7. Так как v = 25077 = r , то В принимает подпись А.

Для криптографической стойкости рекомендуется брать q длиной 160 бит, размер р при любом кратном 64 лежит между 512 (лучше 768) и 1024 бит включительно.

Текст программы:

См. Приложение

Вычисление ключей.

_1.

2.

_3.

_4.

_5.

6. (p = 490663, q = 27259, α = 459706, y = 169635)

Вычисление подписи.

1. h(t) := 1557

2.

_3.

4.

_5.

6. (r = 25077, s = 2895)

Проверка подписи.

1. h(t) := 1557

2. (p = 490663, q = 27259, α = 459706, y = 169635)

3. r = 25077[0, q] s = 2895[0, q]

_4.

5.

6.

7. v = 25077 r = 25077

Московский энергетический институт

(технический университет)