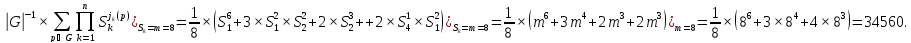- •Курсовая работа по курсу «Комбинаторика»
- •Курсовая работа по курсу «Модулярная арифметика»
- •Курсовая работа по курсу «Графы»
- •2 4 E3
- •Алгоритм построения совершенного паросочетания для двудольного графа.
- •X1 y1
- •X1 y1 Шаг 4.
- •Алгоритм построения совершенного паросочетания в полном нагруженном двудольном графе.
- •X1 y1 x1 0 3 4 3
- •4X1 y1 0 x1 x1 x2
- •7 X2 y2 0 y3 y3
- •8 X3 y3 0
- •7 X4 y4 0
- •3X1 y1 0 x2 x1 x2 x3
- •6 X2 y2 0 y2 y3 y2
- •8 X3 y3 1
- •7 X4 y4 0
- •3X1 y1 0 x3 x1 x2 x3
- •3X1 y1 0 x4 x1 x1 x3 x4
- •6 X2 y2 0 y2 y1 y4 y1
- •7 X3 y3 1 x1
- •6 X4 y4 0 y4
- •3 X1 y1 0
- •6 X2 y2 0
- •7 X3 y3 1
- •6 X4 y4 0
- •Приложение
3 X1 y1 0



6 X2 y2 0


7 X3 y3 1
6 X4 y4 0
G P4 ∑ = 23
Рис. 6
Задача 10.21 Построить плоское изображение графа, если это возможно.
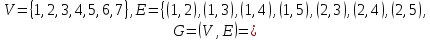

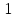


7 2





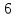 3
3
5
4
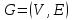
Решение:
Шаг
1.
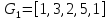
1 3
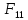
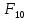
5 2

Граф
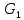 определяет две грани
определяет две грани
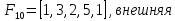

Остаток
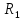 графа
графа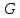 относительно
относительно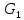 распадается в две компоненты связности
распадается в две компоненты связности


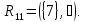
Куски графа
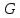 относительно
относительно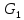 и
их контактные точки
и
их контактные точки
1
 4 2
4 2
3
Кусок
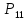 совместим с гранями
совместим с гранями
Выбираем
кусок
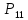 и в нем цепь
и в нем цепь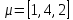
1 3
4



5 2
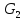
Шаг 2.Плоский граф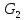 построен
построен
Граф
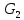 определяет гранью
определяет гранью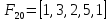
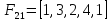
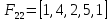
1 3
4




5 2
Остаток
 графаGотносительно
графаGотносительно
Есть

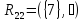
Куски графа
Gотносительно и их контактные точки
и их контактные точки
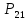 7 4
7 4
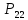 4 3
4 3
Кусок
 совместим с гранью
совместим с гранью
Выбираем
кусок
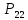 и в нем цепь
и в нем цепь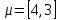
1 3
4




5 2

Шаг 3.
Плоский граф построен
построен
Граф
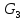 определяется
гранью
определяется
гранью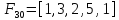

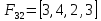
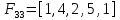
1 3
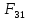
4
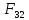





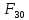
5 2
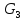
Остаток
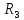 графаGотносительно
графаGотносительно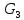
Есть
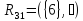
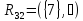
Куски графа
Gотносительно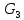 и их контактные точки
и их контактные точки
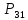 7 4
7 4
Кусок
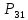 совместим с гранью
совместим с гранью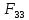
Выбираем
кусок
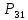 и в нем цепь
и в нем цепь
1 3
4
7





5 2
Шаг 4.
Плоский граф построен
построен
Граф
 определяется
гранью
определяется
гранью
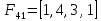

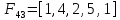
1 3
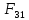
4
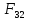
7
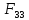






5 2
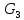
Остаток
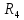 графаGотносительно
графаGотносительно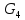
Есть
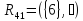
Куски графа
Gотносительно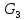 и их контактные точки
и их контактные точки
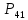 7 6
7 6
Кусок
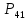 совместим с гранью
совместим с гранью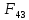
Выбираем
кусок
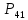 и в нем цепь
и в нем цепь
1 3
4
7 6




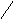


5 2

Шаг 5.
Плоский граф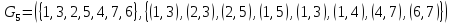
Ни одного
куска относительно графа
 есть плоская укладка графаG.
есть плоская укладка графаG.
Задача 11.21.
В заданном неориентированном графе G найти все максимальные и все наиболее внутренне устойчивые (независимые) множества вершин.
G = (V, E) = (V = {1, 2, 3, 4, 5, 6, 7}, E = {(1,2), (1,3), (1,4), (2,3), (2,4), (2,5), (3,4), (3,5), (3,7), (4,5), (5,6), (5,7), (6,7)}).
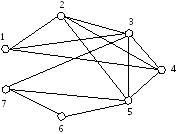
Решение.
Условие внутренней устойчивости графа G:
F
=
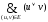 =
(12)(13)(14)(23)(24)(25)(34)(35)(37)(45)(56)(57)(67)
=1235612357124571345713456234572346.
=
(12)(13)(14)(23)(24)(25)(34)(35)(37)(45)(56)(57)(67)
=1235612357124571345713456234572346.
Максимальными внутренне устойчивыми множествами вершин будут множества:
V-{1,2,3,5,6}={4,7}; V-{1,3,4,5,6}={2,7};
V-{1,2,3,5,7}={4,6}; V-{2,3,4,5,7}={1,6};
V-{1,2,4,5,7}={3,6}; V-{2,3,4,6}={1,5,7};
V-{1,3,4,5,7}={2,6}.
Выбираем из них наибольшие: {1,5,7}.
Задача 12.21.
В заданном ориентированном графе G найти все максимальные и все наиболее внутренне устойчивые (независимые) множества вершин.
G = (V, E) = (V = {1, 2, 3, 4, 5, 6, 7}, E = {(1,2), (1,3), (1,4), (2,3), (2,4), (2,5), (3,4), (3,5), (3,7), (4,5), (5,6), (5,7), (6,7)}).

Условие внутренней устойчивости графа G:
F
=
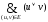 =
(12)(13)(14)(23)(24)(25)(34)(35)(37)(45)(56)(57)(67)
= 1235612357124571345713456234572346.
=
(12)(13)(14)(23)(24)(25)(34)(35)(37)(45)(56)(57)(67)
= 1235612357124571345713456234572346.
Максимальными внутренне устойчивыми множествами вершин будут множества:
V-{1,2,3,5,6}={4,7}; V-{1,3,4,5,6}={2,7};
V-{1,2,3,5,7}={4,6}; V-{2,3,4,5,7}={1,6};
V-{1,2,4,5,7}={3,6}; V-{2,3,4,6}={1,5,7};
V-{1,3,4,5,7}={2,6}.
Выбираем из них наибольшие: {1,5,7}.
Задача 13.21.
В заданном неориентированном графе G найти все минимальные и все наименьшие внешне устойчивые (доминирующие) множества вершин.
G = (V, E) = (V = {1, 2, 3, 4, 5, 6, 7}, E = {(1,2), (1,3), (1,4), (2,3), (2,4), (2,5), (3,4), (3,5), (3,7), (4,5), (5,6), (5,7), (6,7)}).

Условие внешней устойчивости графа G:
F
=
 =
(1234)(21345)(312457)(41235)(523467)
=
(1234)(21345)(312457)(41235)(523467)
(657)(7356) = 151617252627353637454647.
Все минимальные внешне устойчивые множества: {1,5}, {1,6}, {1,7}, {2,5},{2,6}, {2,7}, {3,5}, {3,6}, {3,7}, {4,5}, {4,6}, {4,7}.
Из полученных множеств выбираем наименьшие по мощности. Они составляют все наименьшие внешне устойчивые множества вершин: {1,5}, {1,6}, {1,7}, {2,5},{2,6}, {2,7}, {3,5}, {3,6}, {3,7}, {4,5}, {4,6}, {4,7}.
Задача 14.21.
В заданном ориентированном графе G найти все минимальные и все наименьшие внешне устойчивые (доминирующие) множества вершин.
G = (V, E) = (V = {1, 2, 3, 4, 5, 6, 7}, E = {(1,2), (1,3), (1,4), (2,3), (2,4), (2,5), (3,4), (3,5), (3,7), (4,5), (5,6), (5,7), (6,7)}).

Условие внешней устойчивости графа G:
F
=
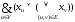 =
(1234)(2345)(3457)(45)(567)
=
(1234)(2345)(3457)(45)(567)
(67) = 152535454647.
Все минимальные внешне устойчивые множества: {1,5}, {2,5}, {3,5}, {4,5}, {4,6}, {4,7}.
Из полученных множеств выбираем наименьшие по мощности. Они составляют все наименьшие внешне устойчивые множества вершин: {1,5}, {2,5}, {3,5}, {4,5}, {4,6}, {4,7}.
Задача 15.21.
Найти хроматическое число графа и оптимальную раскраску графа G.
G = (V,E) = (V={1, 2, 3, 4, 5, 6, 7, 8, 9}, E={(1, 4), (1, 9), (2, 5), (2, 9), (3, 5), (3, 7), (4, 6), (4, 7), (4, 9), (6, 7), (7, 8), (8, 9)})

Условие внутренней устойчивости графа G:
F
=
 =
(14)(19)(25)(29)(35)(37)(46)(47)(49)(67)(78)(89)
=
124578123478123468124567123467457934568923479234689567923679.
=
(14)(19)(25)(29)(35)(37)(46)(47)(49)(67)(78)(89)
=
124578123478123468124567123467457934568923479234689567923679.
Рассматривая полученные дизъюнктивные слагаемые как множества и дополняя их до множества вершин V, получим, что множество S = {S1,S2,S3,S4,S5,S6,S7,S8,S9,S10,S11} =
{{3,6,9}, {5,6,9}, {5,7,9}, {3,8,9}, {5,8,9}, {1,2,3,6,8}, {1,2,7}, {1,5,6,8}, {1,5,7}, {1,2,3,4,8}, {1,4,5,8}}
есть список всех максимальных (тупиковых) внутренне устойчивых множеств вершин графа G.
Условие оптимальной раскраски вершин графа:
R
=
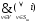 =
(6Ú7Ú8Ú9Ú10Ú11)(6Ú7Ú10)(1Ú4Ú6Ú10)(10Ú11)(2Ú3Ú5Ú8Ú9Ú11)(1Ú2Ú6Ú8)(3Ú7Ú9)
=
(6Ú7Ú8Ú9Ú10Ú11)(6Ú7Ú10)(1Ú4Ú6Ú10)(10Ú11)(2Ú3Ú5Ú8Ú9Ú11)(1Ú2Ú6Ú8)(3Ú7Ú9)
(4Ú5Ú6Ú8Ú10Ú11)(1Ú2Ú3Ú4Ú5) = 2*3*102*7*102*9*101*3*103*6*103*8*101*5*7*105*6*7*105*6*9*105*7*8*102*8*9*101*7*8*104*7*8*104*8*9*101*9*104*6*9*104*8*9*104*6*7*10*112*6*7*112*6*9*113*6*115*6*7*115*6*9*115*6*7*8*114*6*7*8*11
4*6*8*9*111*6*9*114*6*9*114*6*7*111*7*112*4*7*113*4*7*8*11
4*5*6*7*114*5*7*8*114*7*8*114*6*7*9*114*6*7*11.
Из полученных дизъюнктивных слагаемых выбираем наименьшие: 2*3*10, 2*7*10, 2*9*10, 1*3*10, 3*6*10, 3*8*10, 1*9*10, 3*6*11, 1*7*11. Построим оптимальные раскраски вершин графа по множествам {S2,S3,S10}, {S2,S7,S10}, {S2,S9,S10}, {S1,S3,S10}, {S3,S6,S10}, {S3,S8,S10}, {S1,S9,S10}, {S3,S6,S11}, {S1,S7,S11}.
Задача 16.21
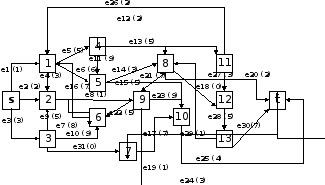
Найти максимальный поток и минимальный разрез между вершинами s и t в транспортной сети с ориентированным графом
G = (V,E), где
V = {s,1,2,3,4,5,6,7,8,9,10,11,12,13,t),
E = {(s,1),(s,2),(s,3),(1,2),(1,4),(1,5),(2,6),(2,9), (3,2),(3,6),(3,7),(4,5),(4,8),
(4,11),(5,8),(5,10),(6,1), (7,10),(7,t),(8,t),(8,9),(8,12),(9,6),(9,10),(9,t),
(10,t),(11,1),(11,12),(12,13),(13,8),(13,t)}.
Вес
wij
дуги
(i,j) равен
N(i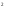 +j
+j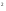 )+i
)+i +
j
+
j +i+j
по
модулю
10
(остаток от деления wij
на 10). N
есть номер варианта.
+i+j
по
модулю
10
(остаток от деления wij
на 10). N
есть номер варианта.
Решение:
Согласно варианту N=21 получаем транспортную сеть S=(V,E,s,t,c) для графа G, где
V = {s,1,2,3,4,5,6,7,8,9,10,11,12,13,t),
E={e1=(s,1,1),e2=(s,2,2),e3=(s,3,3),e4=(1,2,3),e5=(1,4,5),e6=(1,5,6),e7=(2,6,8),
e8=(2,9,1),e9=(3,2,5),e10=(3,6,9),e11=(4,5,9),e12=(4,8,2),e13=(4,11,5),e14=(5,8,3),
e15=(5,10,5),e16=(6,1,7),e17=(7,10,7),e18=(8,12,0),e19=(7,t,1),e20=(8,t,2),e21=(8,9,7),
e22=(9,6,5),e23=(9,10,9),e24=(9,t,3),e25=(10,t,4),e26=(11,1,2),e27=(11,12,3),
e28=(12,13,5),e29= (13,8,1),e30=(13,t,7),e31=(3,7,0)}.
Граф схема транспортной сети S:
Положим начальный поток f0 нулевым. Пометим вершины сети.

Поток f0
Ход от вершин t до вершины s: t, 10, 9, 2, s.
s->2->9->10->t – очередная цепь µ между s и t;
 –направленность
дуг в цепи µ;
–направленность
дуг в цепи µ;
2 1 9 4 – пропускная способность c(e) дуг;
0 0 0 0 – старый поток;
2
1 9 4 –
1
1 1 1 – новый поток
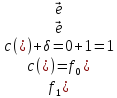
Новый поток f1 и новая разметка вершин сети приведена на рис.2.

Поток f1 (Рис.2)
Ход от вершин t до вершины s: t, 10, 9, 8, 5, 1, s.
s->1->5->8->9->10->t – очередная цепь µ между s и t;
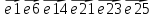 –направленность
дуг в цепи µ;
–направленность
дуг в цепи µ;
1 6 3 7 9 4 – пропускная способность c(e) дуг;
0 0 0 0 1 1 – старый поток;
1
6 3 7 8 3 –
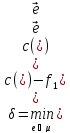
1
1 1 1 2 2 – новый поток
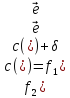
Новый поток f2 и новая разметка вершин сети приведена на рис.3.

Поток f2 (Рис.3)
Ход от вершин t до вершины s: t, 10, 9, 8, 5, 1, 6, 2, s.
s->2->6->1->5->8->9->10->t – очередная цепь µ между s и t;
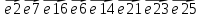 –направленность
дуг в цепи µ;
–направленность
дуг в цепи µ;
2 8 7 6 3 7 9 4 – пропускная способность c(e) дуг;
1 0 0 1 1 1 2 2 – старый поток;
1
8 7 5 2 6 5 2 –
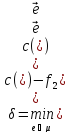
2
1 1 2 2 2 3 3 – новый поток
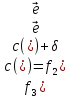
Новый поток f3 и новая разметка вершин сети приведена на рис.4.

Поток f3 (Рис.4)
Ход от вершин t до вершины s: t, 8, 4, 1, 6, 3, s.
s->3->6->1->4->8->t – очередная цепь µ между s и t;
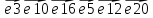 –направленность
дуг в цепи µ;
–направленность
дуг в цепи µ;
3 9 7 5 2 2 – пропускная способность c(e) дуг;
0 0 1 0 0 0 – старый поток;
3
9 6 5 2 2 –

2
2 3 2 2 2 – новый поток
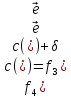
Новый поток f4 и новая разметка вершин сети приведена на рис.5.

Поток f4 (Рис.5)
Ход от вершин t до вершины s: t, 13, 12, 11, 4, 1, 6, 3, s.
s->3->6->1->4->11->12->13->t – очередная цепь µ между s и t;
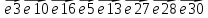 –направленность
дуг в цепи µ;
–направленность
дуг в цепи µ;
3 9 7 5 5 3 5 7 – пропускная способность c(e) дуг;
2 2 3 2 0 0 0 0 – старый поток;
1
7 4 3 5 3 5 7 –
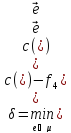
3
3 4 3 1 1 1 1 – новый поток
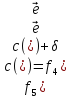
Новый поток f5 и новая разметка вершин сети приведена на рис.6.

От s до t новой цепи построить не удается (e1,e2,e3 – полностью насыщены). Вершина t пометки не получила. Последний поток f5 есть максимальный поток и величина потока Mf5=8. Максимально возможная величина потока (нагружающая дуги истока, равно как и дуги стока) Mfmax=8.
Минимальный разрез MS={e21, e30, e24, e26, e19}.
Ответ:
MS={e21, e30, e24, e26, e19}, Mfmax=8.
Задача №17.21
Найти число ожерелий, которые можно составить из семи бусин не более чем m цветов. Число цветов m равно числу букв в фамилии студента. Бусины обозначить буквами фамилии. Недостающие буквы взять из алфавита.

Решение:
Ожерелье типа (n,m) есть правильные n – угольник, вершины которого раскрашены в не более чем k цветов.
Два ожерелья неотличимы (одинаковы), если одно можно получить из другого, поворачивая его относительно точки симметрии или симметрично отражая относительно одной из осей симметрии.
Для подсчета числа ожерелий типа (n, m) нужно найти группу G вращений и симметрий правильного n-угольника, которая есть некоторая группа подстановок на множестве Х = {1, 2, …, n}, потом составить многочлен циклов, а затем применить теорему Пойа.
Подсчитаем число ожерелий, которые можно составить из семи бусин не более чем m = 8 цветов.
Для перечисленных операций соответствующая группа G состоит из 14 подстановок.
Повороты:
p0=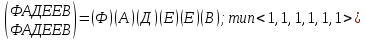
p1
=
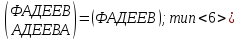
p2
=
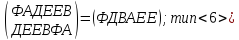
p3
=

p4
=

p5
=

Симметрия относительно прямых, проходящих через вершины и середины противоположных сторон:
p6
=
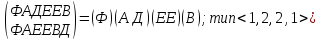
p7
=
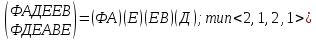
p8
=

p9
=
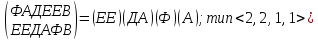
p10
=
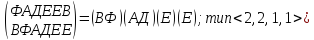
p11
=
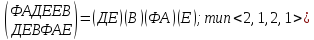
p12
=
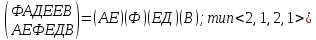
Мы получили следующее:
1 подстановка типа <1, 1, 1, 1, 1, 1> соответствует слагаемому S17 многочлена циклов;
6 подстановок типа <6> соответствуют слагаемому 6×S71 многочлена циклов;
7 подстановок типа <1, 2, 2, 2 > соответствуют слагаемому 6×S11×S23 многочлена циклов;
По теореме Пойа многочлен циклов:
N(G)
=
 .
.
Из семи бусин не более чем m=8 цветов можно составить:
N(G)
=
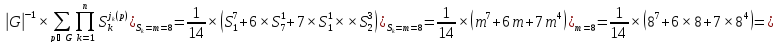
 .
.
Задача №18.21
Найти число различных раскрасок вершин многогранника М в не более чем m цветов. Многогранник М составлен из двух одинаковых правильных четырехугольных пирамид, с общим основанием и вершинами, расположенными по разные стороны от основания. Число цветов m равно числу букв в фамилии студента. Вершины многогранника обозначит буквами фамилии. Недостающие буквы взять из алфавита.

Д
Решение:
Две раскраски считаются одинаковыми, если вращением многогранника М в пространстве их раскраски можно совместить. Шесть вершин нашей фигуры не более чем восемью красками можно раскрасить 86 = 262144 способами. Многие раскраски окажутся одинаковыми.
Для вычисления числа раскрасок вершин фигуры нужно вычислить группу G вращений многогранника:
Повороты относительно прямой, проходящей через центр основания:
p0
=
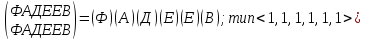
p1
=

p2
=

p3
=
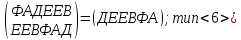
Симметрия относительно диагоналей в основании:
p4
=
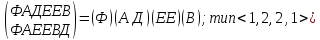
p5
=

Симметрия относительно прямых, проходящих через середины сторон основания:
p6
=

p7
=
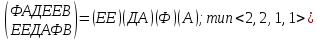
В группе подстановок вращений G фигуры:
1 подстановка типа <1, 1, 1, 1, 1, 1 > соответствует слагаемому S16 многочлена циклов;
3 подстановки типа < 1, 1, 2, 2 > соответствуют слагаемому 3×S12×S22 многочлена циклов;
2 подстановки типа < 2, 2, 2 > соответствуют слагаемому 2×S23 многочлена циклов;
2 подстановки типа < 4, 1, 1 > соответствуют слагаемому 2×S41×S12 многочлена циклов;
По теореме Пойа многочлен циклов:
N(GМ)
=
 .
.
Число различных раскрасок вершин фигуры в не более чем m=9 цвета есть число:
N(GМ)
=