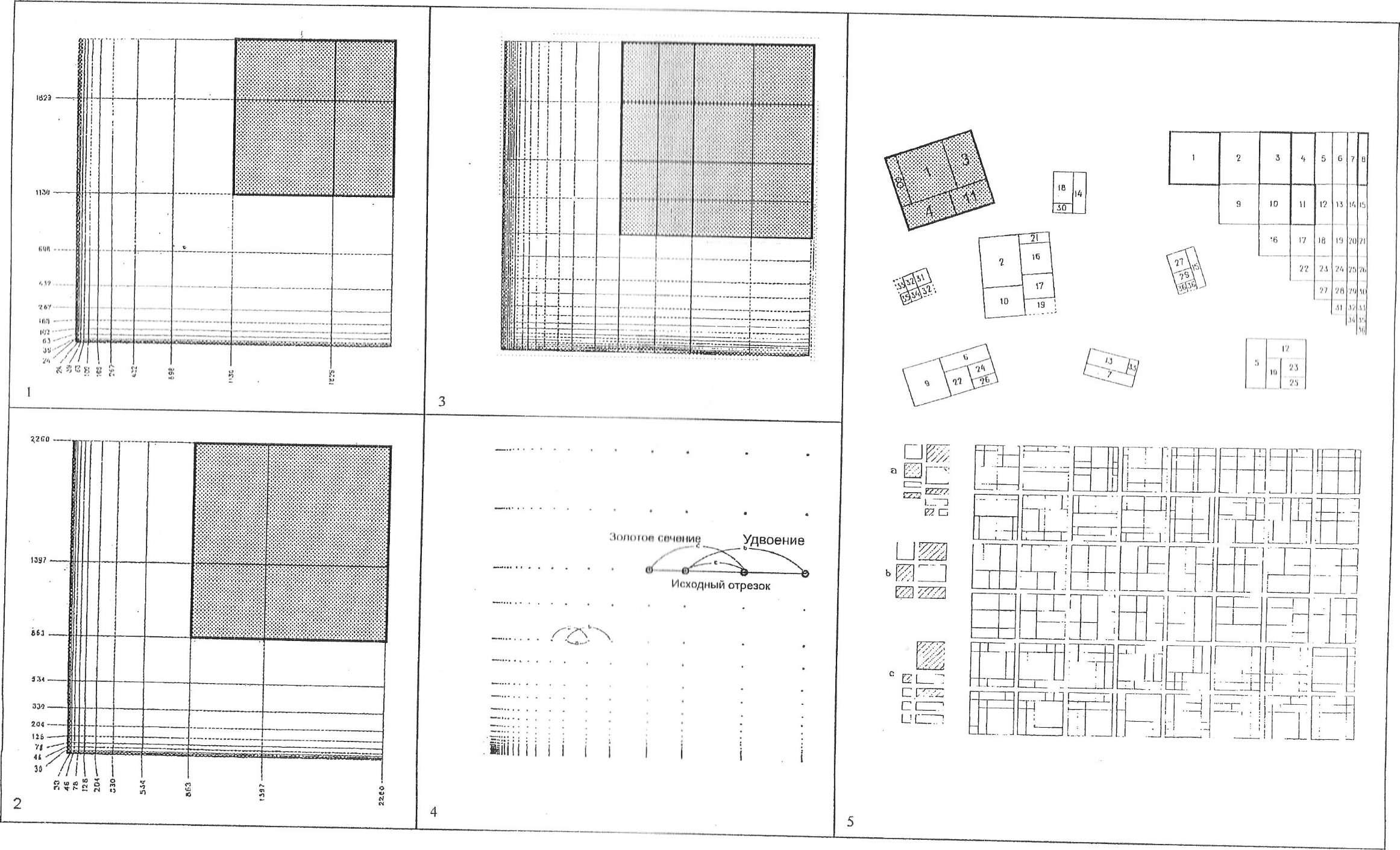
1. Пропорционирование

Пропорционирование — это использование пропорций для организации формы в целостную структуру, т.е. применение определенного способа количественного согласования частей и целого.

Пропорциональная зависимость может быть выражена величинами, располо­женными: а) по одной координате, б),в) по двум координатам, г) по трем коорди­натам.

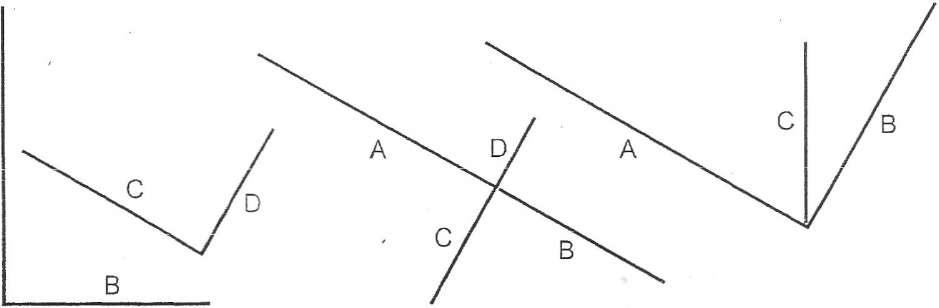
А) Б) В) Г)

В подобных прямоугольниках диагонали или параллельны (прямая пропор­ция) или перпендикулярны друг другу (обратная пропорция). На этом основан геометрический метод построения пропорций (рис. а, б.).

Линии при помощи которых устанавливается подобие (диагонали) Ле Кор­бюзье назвал регулирующими линиями. «Выбор регулирующих линий фиксиру­ет основную геометрию произведения... Подлинные регулирующие линии те, с помощью которых удается привести в согласие каждый отдельный элемент со всем целым, детали друг с другом, найти математическое отношение, способное вдохнуть душу равно во все элементы сооружения... Выбор регулирующих линий относится к решающим моментам вдохновения, это одна из капитальных опера­ций архитектуры».

На рисунках в), г), д) приведены примеры построения членений формы в за­кономерной связи с высотой и шириной самих форм. Каждое построение пропор­ций во всем своем многообразии обусловливается композиционным решением в целом.

А)

ОБРАТНАЯ ПРОПОРЦИЯ

РАСЧЛЕНЕНИЕ СОПОДЧИНЕНИЕ

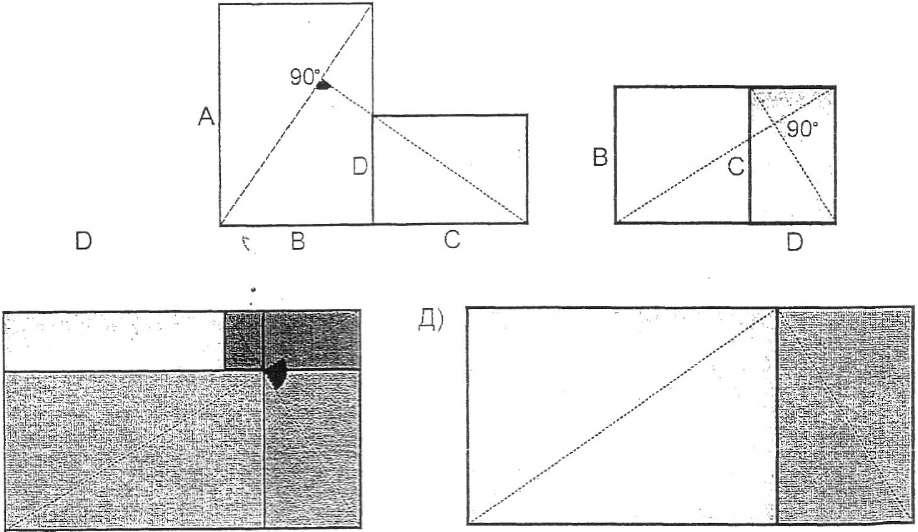
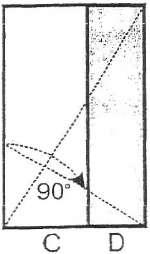
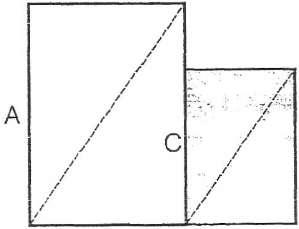
ПРЯМАЯ ПРОПОРЦИЯ

/

Построение пропорционального ряда «золотого сечения».

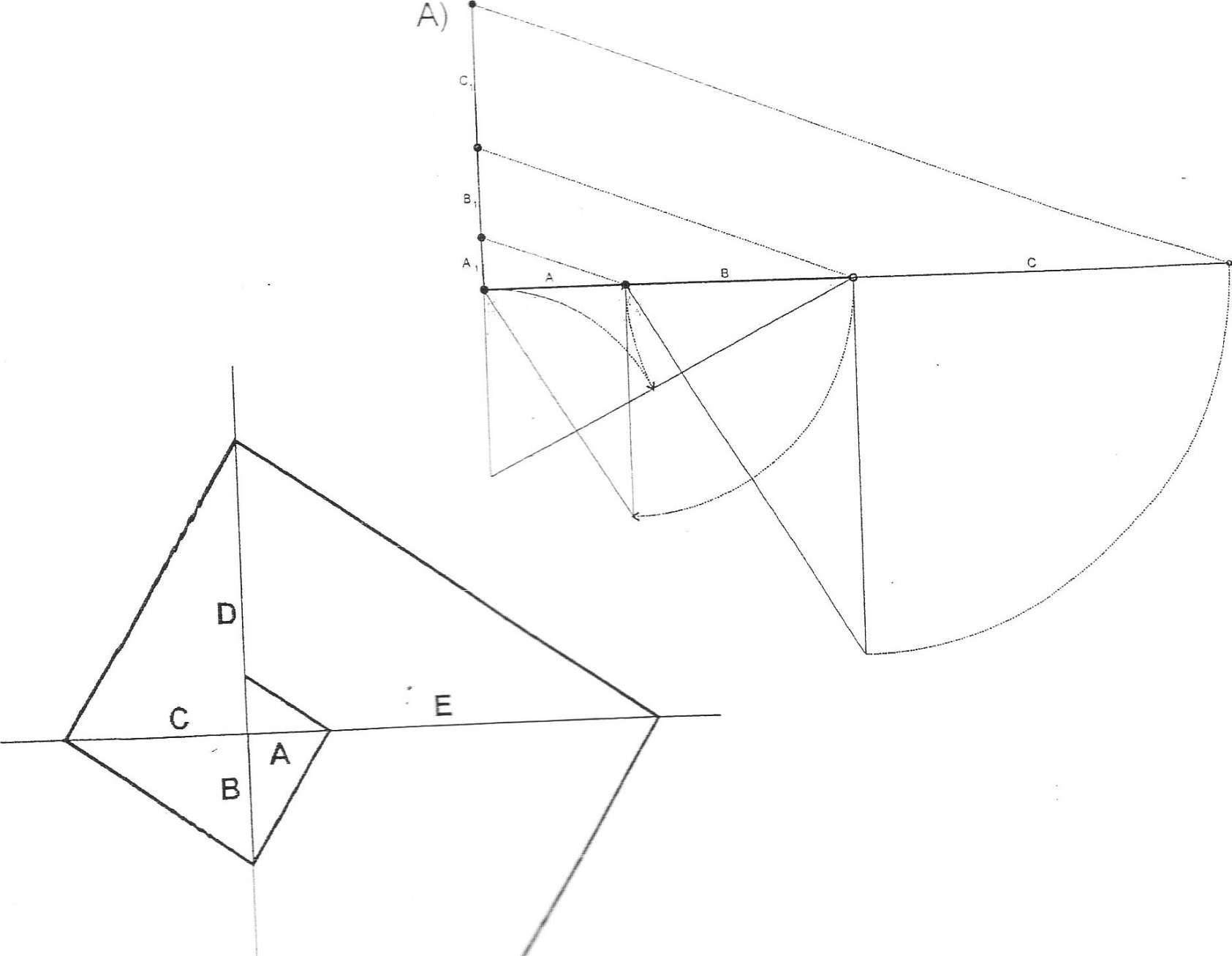
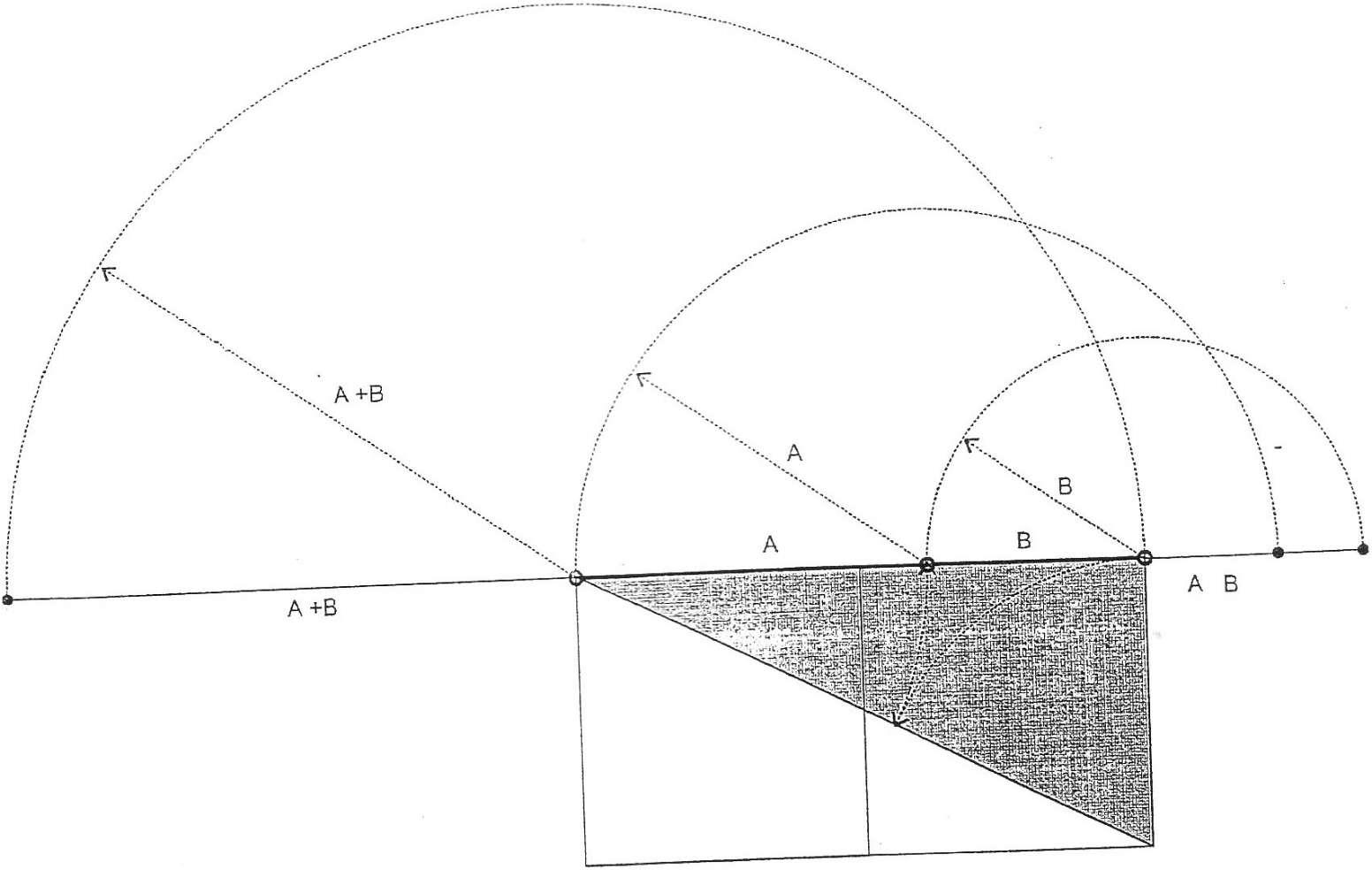
Построение геометрически пропорционального ряда по заданному отноше- нию между отрезками А и В:

Литература для 1 курса по теме «Пропорции». Теории пропорций. Краткий обзор.

Общие:

2. Петрович Д. Теоретики пропорций. М., 1979 г.

'3. Авксентьев В.Л. Архитектурная пропорция. К., 1986 г.

2. Основы архитектурной композиции и проектирования. К.,1976 (стр.149-173)

Персоналии:

1 Мёссель Э. Пропорции в античности, и в средние века. М_м 1936 г.

2. Врунов Н.И. Пропорции в античной и средневековой архитектуре. М., 1935 г,

3. Гурьев О.И. Композиция Андреа Палладио. Вопросы пропорциональности. Л.,1984 г.

4. Палладио Андреа. Четыре книги об архитектуре. М., 1936 г.

5. Хэмбидж Э. Динамическая симметрия в архитектуре. М.,1936 г.

6. Гика М. Эстетика пропорции в природе и искусстве. М., 1936 г.

7. Ле Корбюзье. Модулор М-1, М-2. М.. 1976 г.

8. Шевелев И.Ш. Геометрическая гармония. К., 1963. Логика архитектурной гар­монии. М., 1973. Принцип пропорции. М., 1986 г.

9. Krier Rob. «Immeuble dihabitation Ritterstrasse. Berlin». / [.'Architecture d'haujourdhui. T-1, № 213.1986 г./

Модулор ле корбюзье

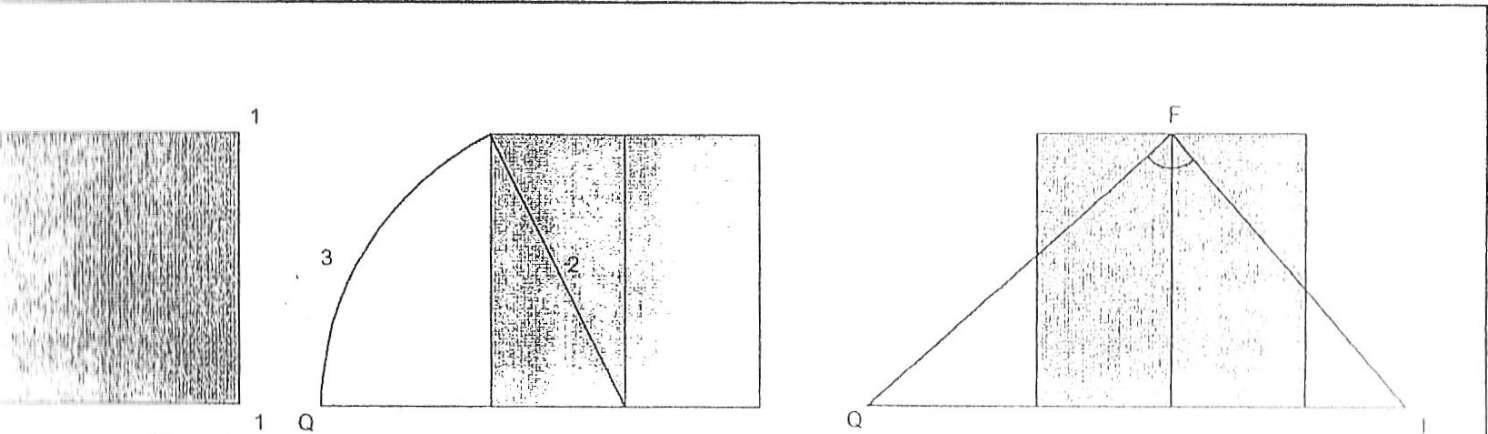
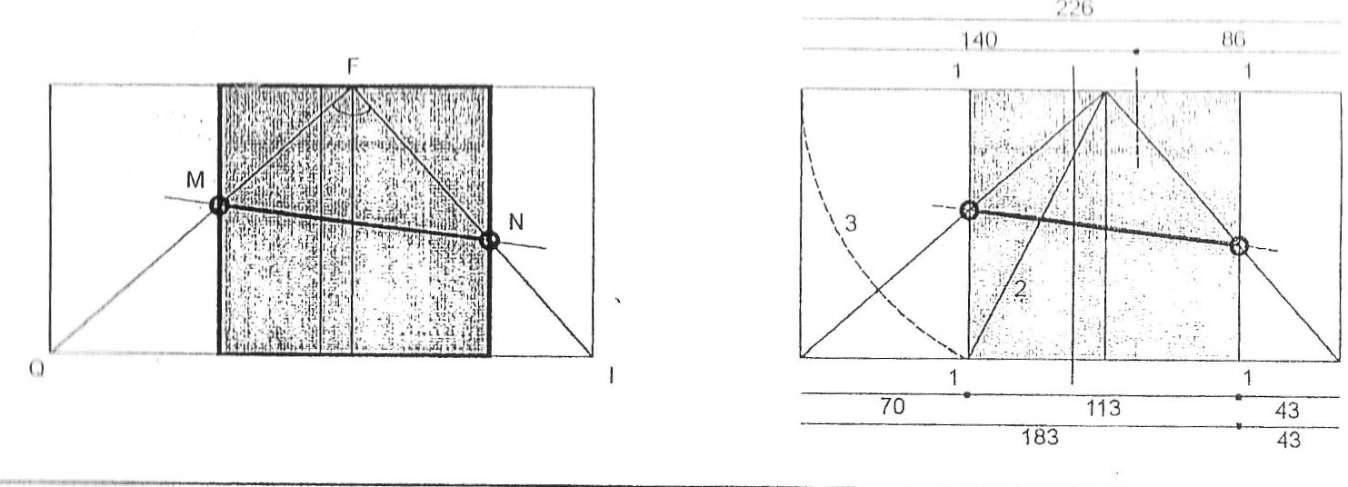
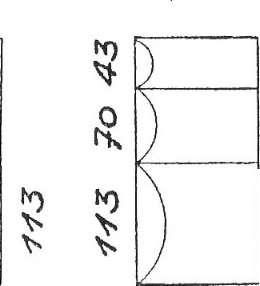
По мнению Ле Корбюзье - вы­дающегося французского архи­тектора XX века, новый инст­румент пропорционнроваиия архитектурных форм должен явиться основным средством объединения и сочетания чело­веческого труда, разобщенного присутствием двух труднопри- миримых между собой систем: антропоцентрической англосак­сонской фут - дюйм (фут — сто­па, дюйм — большой палец), с одной стороны, п абстрактной метрической (метр - сорока- миллнонная часть земного ме­ридиана) с другой. «Модулор» - это средство измерении, осно­вой которого является рост человека и математика. Чело­век с поднятой рукой дает нам точки, определяющие занятое им пространство - нога, солнеч­ное сплетение, голова, кончик пальцев поднятой руки, - три интервала, обусловливающие серию золотого сечения, назы­ваемую рядом Фибоначчи. С другой стороны, математика предлагает здесь некоторое изменение, очень простое и в то же время весьма существенное: простой квадрат, удвоение и два золотых сечения.(рис.1). Окон­чательный вариант «Модулора» основывается на росте человека в 6 футов (182,9 см.) 1). Три размера: 113, 70, 43 (в сантимет­рах), которые согласуются с Ф (золотое сечение) и рядом Фи­боначчи: 43 + 70 = 113, или ИЗ - 70 = 43. В сумме они дают: 113 + 70 = 183; 113 + 70 + 43 = 226.

2. . Эти три размера (113 - сол­нечное сплетение, 183 - верши­на головы, 226 - конец пальцев поднятой руки) определяют величину пространства, зани­маемого человеком шести футов

3. . Размер 113 определяет золо­тое сечение 70, показывая нача­ло первой красной серии: 4 - 6 - 10 -16 - 27 - 43 - 70 - 113 - 183 - 296 и т.д. Второе отношение Ф, 140 - 86, вводит четвертую су­щественную точку фигуры че­ловека — точку опоры опущен­ной руки: 86 сантиметров. Раз­мер 226 (2 х 113 - удвоение) определяют золотое ссчспне 140 - 86, показывая начало второй, синей серии: 13 - 20,3 - 33 - 53 - 86 - 140 - 226 - 366 - 592 и т. д. (рис. 2) Из таблицы видно, что отсчет числовых значений «Мо­дулора» ведется вниз и вверх от горизонтальной линии, прове­денной под числом 113, которое и «порождает» ряд красной серии. Исходные величины в «Модулоре» закономерно раз­биваются на более мелкие. Каж­дый отрезок красной серии ра­вен половине одного из отрезков синей серии. Таким образом, в цепи «Модулора» возникает связь золотого ряда и сдвоенно­сти. «Модулор» благодаря сво­им комбинационным возможно­стям является как бы клавиа­турой, которая позволяет сыг­рать большое количество гамм, где каждый элемент связан с соседним и всеми остальными в единое целое.

«I

В метрической системе мер				В дюймовой системе мер
' красный ряд		синий ряд		красный ряд	синий ряд
см	м	см	м

95	280,7
58	886,7
36	894,0
22	402,7
18	901,3
8	591,4
5	80», 8
3	281,6
2	028,2
1	258,5
	774,7
	478,8
	295,9
	182,9
	113,0
	69,8
	43,2
	26,7
	16,5
	10,2
	6,3
	8,9
	' 2,4
	1,5
	0,9
	0,6

952,80 588,86 363,94 224,92 139y0f 85,91 53,10 32,81 20,28 12,53 7,74 4,79 2,96 1,83 1,13

117 773,5 72 788,0 44 985,5 27 802,5 17 182,2 10 619,6 6 563,3 4 056,3 2 506,9 1 549,4 957,6 591,8 365,8 226,0

1177,73 727,88 449,85 278,02 171,83 106,19 65,63 40,56 25,07 15,49 9,57 5,92 3,66 2,26

139,7

4. 33,0 20,4 12,6

7,8 4,8

0. 1,8

0,70 0,43 *0,26 0,16 0,10 0,06 0,04 0,02 0,01

1,40 0,86 0,53 0,38 0,20 0,12 0,08 0,04 0,08 0,01

304"962(805") 188"479<188"*Л) 116"491 (116*7,) 72*000(72'') 44*497(44" V»)

27"499(27"¹/*)

16 "906(17")

10 "Boeiio"*/*) 6"495(0"^,/i)

• C>

609*931(610") 376*966(377") 232*984(233") 143*994(144") 88*993(89") 55"000(55")

83^,,992(34") 21*007(21") 12*988(13") 8"Q28(8")

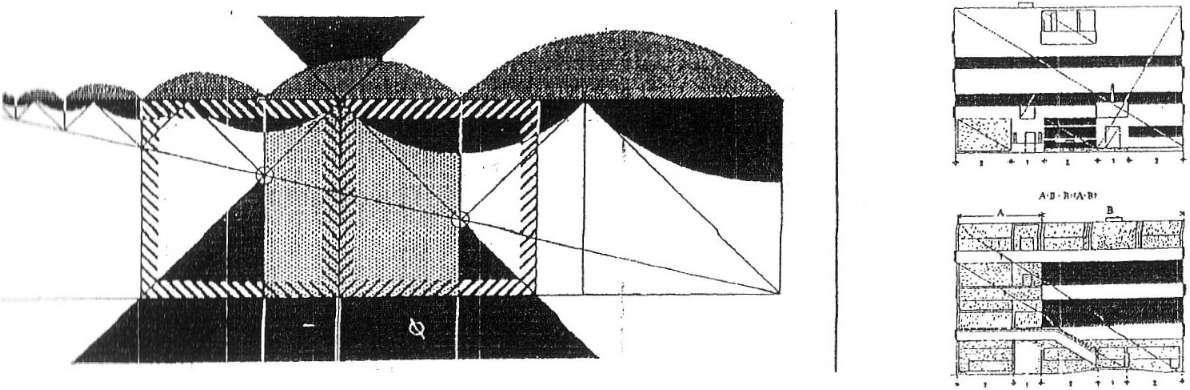
1. СЕТКА "МОДУЛОРА", ПОСТРОЕННАЯ НА ОСНОВЕ КРАСНОГО РЯДА.

2. СЕТКА "МОДУЛОРА", ПОСТРОЕННАЯ НА ОСНОВЕ СИНЕГО РЯДА.

3. СОВМЕЩЕ ИНАЯ СИ ПСА КРАСНОГО И СИНЕ­ГО РЯДОВ.

4. ТОЧКИ ЛЕРЕСЕЧП11ИЯ СЕТОК, ОПРЕДЕЛЯЮ­ЩИЕ ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ.

5. РАЗЛИЧНЫЕ ВАРИАНТЫ ЧЛ, ПЛОСКОСТИ НА ОСНОВЕ ПЕРь НИЯ СЕТОК КРАСНОГО И СИНЕГО 1 ДОВ.