
/j^^utSt 2
®
Тема: Пропорции. План лекции:
-
Введение. Гармония как эстетическая категория.
-
Простые и иррациональные отношения. Подобие.
-
Типы пропорций. Пропорционирование.
1. Введение. Гармония как эстетическая категория.
В VI веке до нашей эры, ученики Пифагора абсолютизировали найденные ими числовые отношения, положив их в основу учения о гармонии мира - «гармонии сфер». Они полагали, что гармония между микрокосмосом и макрокосмосом определяется математическими законами пропорционального единства. Пифагорейцы представляли числа не только абстрактно но и пластически - в виде определённых геометрических тел. «Следовательно, числовое становление мыслилось пифагорейцами как становление прежде всего космических тел, издающих при своём движении определенного рода тоны с гармоническим сочетанием этих тонов в одно прекрасное и вечное целое»,- замечает А.Ф.Лосев.
В эстетике эллинизма (между 323 и 30 годами до н.э.) учение о гармонии развивалось не только применительно к музыке, но и по отношению к другим видам искусства, в частности к живописи и архитектуре. Витрувий (вторая половина 1 века до н.э.) считал, что понятие архитектуры раскрывается посредством следующих шести элементов: строя (ordinatio), расположения (dispositio), эвритмии (euritmia), благообразия (decor), расчета (distributio), соразмерности (summetria). Среди них главным является понятие соразмерности. Впрочем эвритмия, также как и пропорция, тоже является видом соразмерности, но в отличие от пропорции это - внешний тип соразмерности, соразмерность полученная при восприятии внешнего вида архитектурного объекта.
Гармония была одним из важнейших понятий в истории эстетики и занимала одно из центральных мест в системе эстетических категорий. Можно выделить по крайней мере три типа понимания гармонии, которые фигурировали на протяжении всей истории эстетической мысли,- математическое, эстетическое и художественное. В математическом смысле гармония понималась как равенство или соразмерность частей друг с другом и части с целым и выражалась в виде определенных числовых пропорций.
Миф о пропорции, или как её называл современник и друг великого Леонардо да Винчи Лука Пачоли (итальянский математик, живший ок. 1445 г.), - «божественной пропорции», является очевидно одним из наиболее древних в истории профессии. О ней удивительно много написано, исследованию различных аспектов пропорции посвятили свои труды выдающиеся зодчие и теоретики архитектуры. Необходимость изучения пропорций обосновывалась самыми различными способами: теологическим, эстетическим, антропологическим, математическим и т.д. Но во всём этом обширном и невообразимо пёстром материале мы должны, исходя из задач нашей дисциплины, выделить и зафиксировать геометрический и специфический инструментальный аспекты архитектурной пропорции, создав тем самым предпосылки для практического освоения этого важнейшего средства профессиональной деятельности.
I s I
![]()
2. Простые и иррациональные отношения. Подобие.
Если в математике под отношением понимают частное от деления одной величины на другую, то понятие отношения в архитектуре гораздо шире и включает в себя все виды взаимосвязи величин, характеризующих объективные свойства формы.
В архитектуре, так же как и в математике, различают два вида закономерных или гармонических отношений пространственных величин: рациональные или простые и иррациональные.
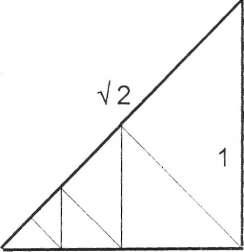
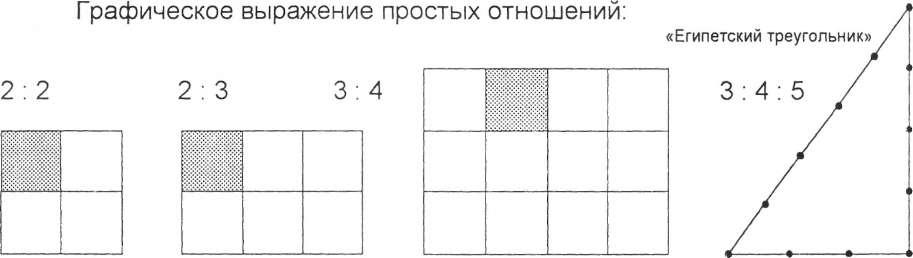
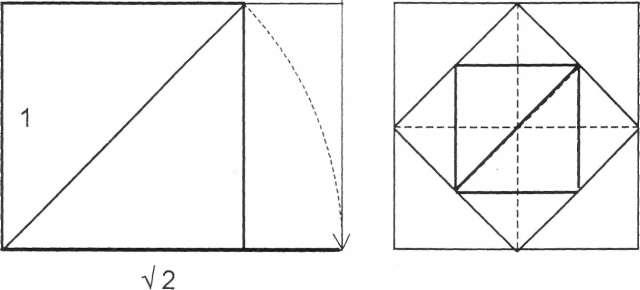
2.2. Иррациональные отношения не могут быть выражены конечным числом и основываются на простой геометрической закономерности их построения. Графическое выражение иррациональных отношений: а). Отношение диагонали квадрата к его стороне а : в = 1 : V2. Сторона описанного квадрата равна диагонали вписанного. 1
б). Отношение высоты равностороннего
треугольника к половине его основания
а : в = 1 : V3.
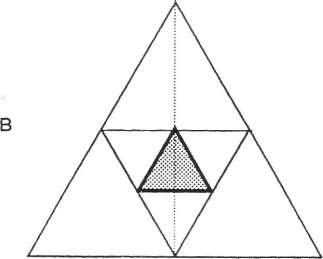
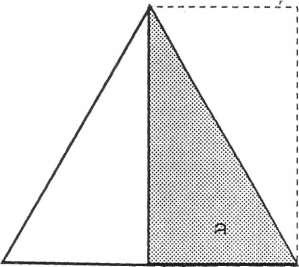
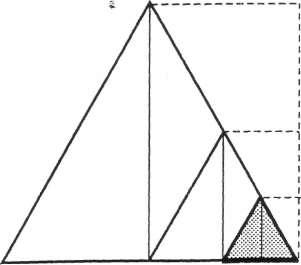
1
в). Отношение, называемое «золотым
сечением» а : б = 1,62..
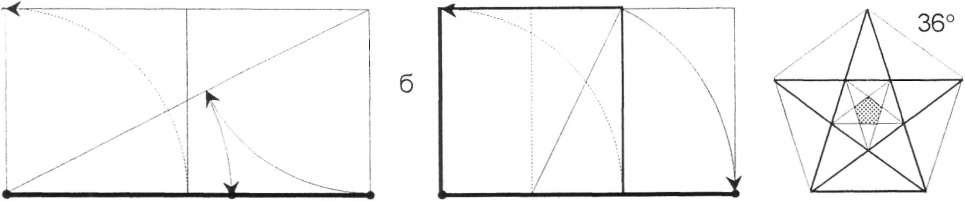
а б а 72° 72°
Пифагорейское учение о гармонии было связано с музыкальной теорией, акустикой и теорией звука. Была высказана идея о связи высоты тона с быстротой движения и частотой колебаний. Архит заметил, что высота тонов зависит от длины струны, причём она изменяется в отношении обратнопропорциональном к этой длине. Т.е. чем выше тон, тем меньше длина струны.
Отношение колебаний
Интервалы тонов и длины струны
2.3. Подобие.
Наиболее общим признаком наличия пропорциональной зависимости служит геометрическое подобие (греч. analogia - соответствие) отрезков и фигур. Там, где есть подобие, есть и пропорции; где подобия нет, там нет и пропорционпльнлсти элементов формы.
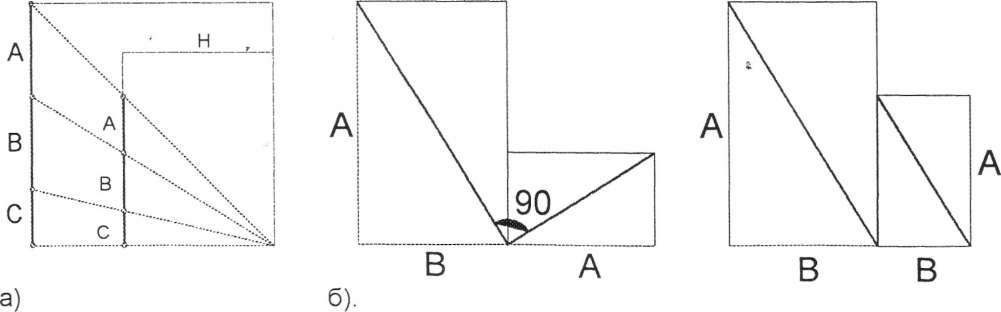
На схеме а), показана геометрическая зависимость двух линейных элементов, расчлененных в отношении: A:a=B:B = C:c=H:h. Взаимосвязь между элементами достигается благодаря подразделению их на геометрически подобные части (теорема о подобии треугольников)
На схеме б)., при равенстве отношений А : В = а : в, приходится иметь дело уже не столько со сходством или подобием отрезков, сколько с геометрическим подобием фигур. Параллельное или перпендикуляроне расположение диагоналей сходных и соответственно расположенных фигур служит подтверждением геометрического подобия последних.
Н
3 Типы пропорций.
Пропорция (лат. proportio) математич. - есть равенство двух отношений.
«...но невозможно сочетать две вещи без наличия третей: между ними необходим связующий элемент. Нет лучше связи, чем та, которая образует из самой себя и связуемых ею вещей одно неделимое целое. И такова природа пропорции»^ Платон., «Тимей».)
Пропорция в архитектуре есть понятие, отражающее однородность (закономерность) изменений количественной меры при переходах от одной части формы к другой, и к форме в целом.
Пытаясь определить числовую величину музыкальных интервалов, пифагорейцы (Архит) пришли к учению о трех типах пропорций - арифметической, геометрической и гармонической.
Арифметические (модульные) пропорции основаны на арифметической прогрессии. Взаимосвязь частей и целого осуществляется повторением единого заданного размера, полученного в виде разности каждой пары членов:
(а - в) = (в - с) = ... = М (модуль). С-В = С
В-А С например: !, 2, 3, 4,...; 6, 9, 12... .
Геометрические (непрерывные) пропорции основаны на геометрической прогрессии. Взаимосвязь частей и целого осуществляется при равенстве отношений между членами:
(а : в) = (в : с) =...= К (коэффициент).
С-В = С
В-А В например: 1, 2, 4, 8,..., 4, 6, 9,... .
Гармонические пропорции являются разновидностью геометрических. Они основываются на гармонической прогрессии, представляющей собой ряд чисел обратных ряду чисел арифметической прогрессии, например: 1/3, !/4, 1/5, 1/6, 1/7, .
С-В = С
В-А А например: 2, 3, 6, ... , 6, 8, 12,... .
