
- •17. Дифференциальное исчисление
- •17.1. Дифференцирование функции с переменной
- •I уровень
- •II уровень
- •III уровень
- •17.2. Дифференцирование функций, заданных
- •I уровень
- •II уровень
- •III уровень
- •17.3. Необходимое и достаточное условия
- •I уровень
- •II уровень
- •III уровень
- •17.4. Производные и дифференциалы высшего
- •I уровень
- •II уровень
- •III уровень
- •17.5. Правило Лопиталя. Формула Тейлора
- •I уровень
- •II уровень
- •III уровень
- •17.6. Исследование функций. Наибольшее
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1.
Вычислите дифференциал функции
![]() в точке
в точке![]() при заданном значении
при заданном значении![]()
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
1.2.
Найдите главную часть приращения
![]() функции
функции![]() в точке
в точке![]()
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
1.3. Вычислите дифференциал функции:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
1.4.
Вычислите приближенно с помощью
дифференциала значение функции
![]() в точкеx:
в точкеx:
1)
![]() 2)
2)![]()
![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
II уровень
2.1.
Вычислите дифференциал функции
![]() в точке
в точке![]() если аргумент изменяется от
если аргумент изменяется от![]() до
до![]()
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
2.2. Вычислите дифференциал функции:
1)
![]() 2)
2)![]()
3)
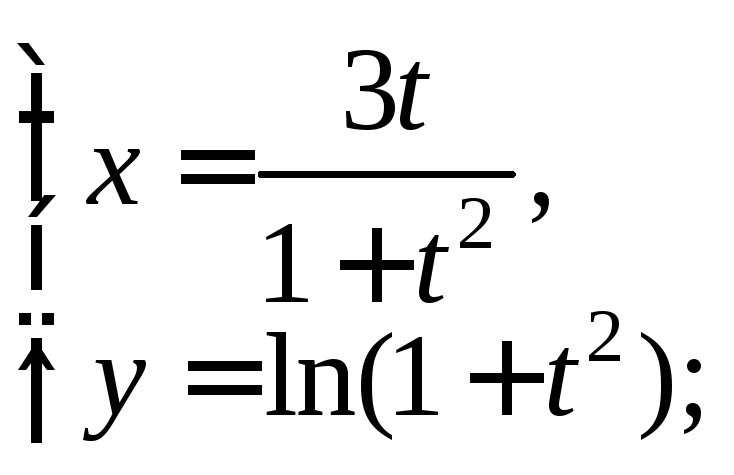 4)
4)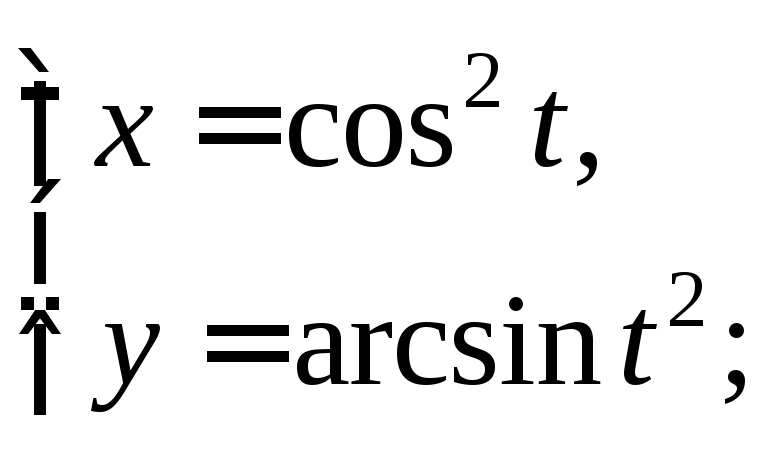
5)
![]() 6)
6)
![]()
2.3.
Проверьте, удовлетворяет ли функция
![]() заданному уравнению:
заданному уравнению:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
2.4. Вычислите с помощью дифференциала приближенное значение выражения:
1)
![]() 2)
2)![]() 3)
3)![]()
4)
![]() 5)
5)![]() 6)
6)![]()
2.5. Даны два тетраэдра, ребра которых равны соответственно 4 и 4,21. Определите, на сколько объем первого тетраэдра меньше объема второго.
2.6. Определите, на сколько увеличится при нагревании объем куба, ребро которого равно 10 см, если удлинение ребра куба равно 0,03 см.
2.7. Сторона квадратного листа жести, равная 15 см, после охлаждения уменьшилась на 0,001 см. Вычислите приближенно, на сколько изменилась площадь этого листа.
III уровень
3.1.
Докажите, что функция
![]() заданная в неявном виде уравнением
заданная в неявном виде уравнением![]() удовлетворяет уравнению:
удовлетворяет уравнению:
1)
![]() если
если![]()
2)
![]() если
если![]()
3)
![]() если
если![]()
3.2. Вычислите приближенно значение выражения:
1)
![]() 2)
2)![]()
3.3. Боковую поверхность стального конуса с диаметром основания 20 см и высотой 10 см отшлифовали, после чего диаметр стал равен 19,95 см. Определите, на сколько приблизительно изменилась масса конуса, если плотность стали равна 7,80 г/см3.
17.4. Производные и дифференциалы высшего
порядка
Производная
![]() определенная на некотором множестве
определенная на некотором множестве![]() является также функцией отx.
В случае ее дифференцируемости можно
вычислить ее производную. Производная
от производной
является также функцией отx.
В случае ее дифференцируемости можно
вычислить ее производную. Производная
от производной
![]() называетсяпроизводной
второго порядка:
называетсяпроизводной
второго порядка:
![]()
Аналогично
![]()
Начиная с четвертого,
порядок производной обозначают в скобках
(сверху):
![]() Производные порядка 1–3 также обозначают
Производные порядка 1–3 также обозначают![]()
![]()
![]() По определению
По определению![]() В случае дифференцируемости производной
В случае дифференцируемости производной![]()
![]() производная порядкаn
определяется равенством
производная порядкаn
определяется равенством
![]() (17.12)
(17.12)
Для производных высшего порядка справедливо свойство линейности:
![]()
где
![]() – произвольные действительные числа;f(x),
g(x)
– n
раз дифференцируемые функции,
– произвольные действительные числа;f(x),
g(x)
– n
раз дифференцируемые функции,
![]()
Если f(x)
и g(x)
– n
раз дифференцируемые функции,
![]() то вернаформула
Лейбница:
то вернаформула
Лейбница:
![]() (17.13)
(17.13)
где
![]() – биномиальные коэффициенты:
– биномиальные коэффициенты:![]()
Коэффициенты
![]() можно найти также из треугольника
Паскаля.
можно найти также из треугольника
Паскаля.
Если функция у(х)
задана в неявном виде уравнением
![]() то для нахождения производной второго
порядка (в случае ее существования)
надо продифференцировать найденную
первую производную по аргументуx,
продолжая рассматривать y
как функцию от x.
Затем вместо
то для нахождения производной второго
порядка (в случае ее существования)
надо продифференцировать найденную
первую производную по аргументуx,
продолжая рассматривать y
как функцию от x.
Затем вместо
![]() надо подставить найденное ранее значение.
надо подставить найденное ранее значение.
Если функция задана параметрически в виде
![]()
то находят вначале производную 1-го порядка по формуле (17.6) и записывают:
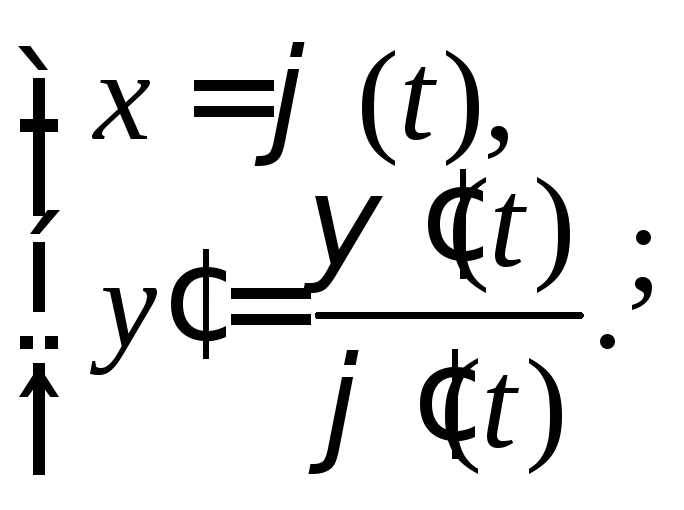 (17.14)
(17.14)
Для нахождения производной второго порядка используют формулу (17.6) к параметрически заданной функции (17.14):

Аналогично реализуют
тот же подход при нахождении производной
![]() и т. д.
и т. д.
Дифференциал от дифференциала функции f в точке x (если функция определена и дважды дифференцируема) называется дифференциалом второго порядка:
![]()
Дифференциал n-го
порядка функции f(x)
(в случае дифференцируемости n
раз,
![]() )
определяют как дифференциал от
дифференциала (n–1)-го
порядка:
)
определяют как дифференциал от
дифференциала (n–1)-го
порядка:
![]()
![]()
Для вычисления дифференциала порядка n используют формулу
![]() (17.15)
(17.15)
Дифференциалы второго и выше порядков не обладают (в отличие от дифференциалов первого порядка) свойством инвариантности, т. е. их форма, а следовательно, и способ вычисления зависят от того, является ли аргумент x независимой переменной или дифференцируемой функцией другой переменной.
Пример 1.
Вычислить
![]() для функции:
для функции:
1)
![]() 2)
2)![]()
Решение. 1) Вычислим искомую производную последовательно, не применяя формулу Лейбница:
![]()
![]()
![]()
![]()
2) Искомую производную удобно найти, используя формулу Лейбница (17.13). Для производной 4-го порядка формула Лейбница примет вид:
![]()
Функцию
![]() представим в виде
представим в виде![]() Введем обозначения:
Введем обозначения:![]()
![]() Для функцииf(х)
найдем производные:
Для функцииf(х)
найдем производные:
![]()
![]()
![]()
![]()
Аналогично для функции g(x) найдем производные:
![]()
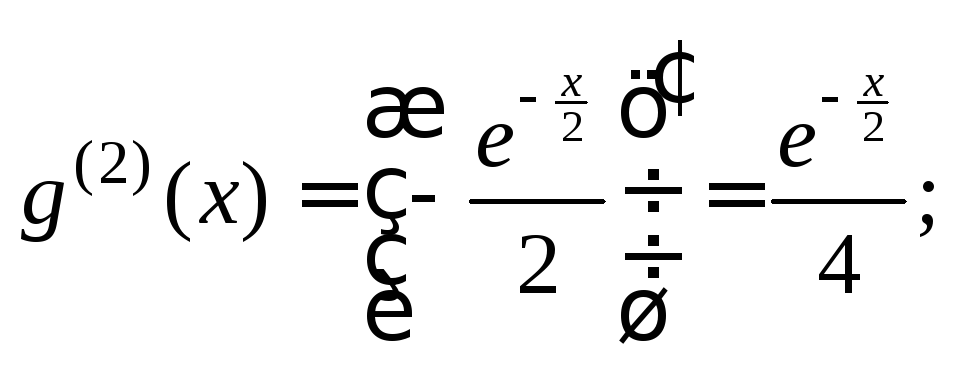
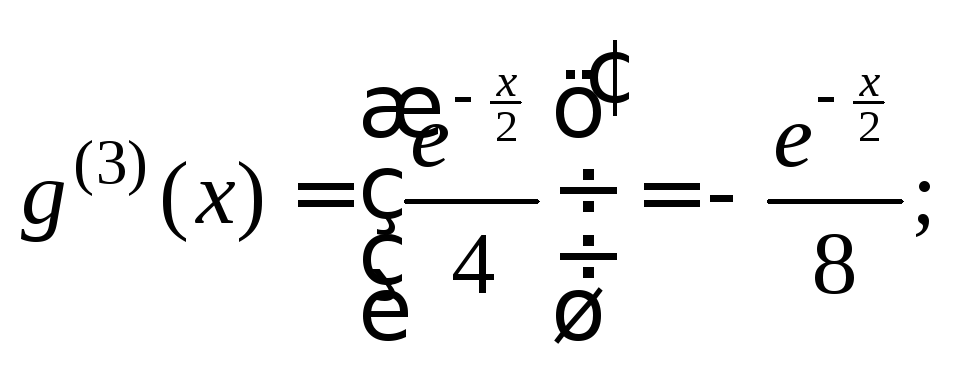
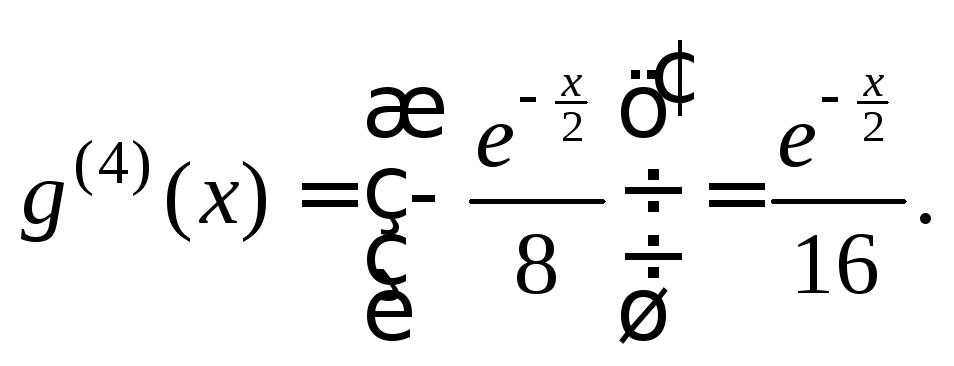
Полученные выражения подставим в формулу Лейбница:

![]()
Упрощая это выражение, окончательно получим:
![]()
Пример 2.
Для функции
![]() найти формулу производнойn-го
порядка,
найти формулу производнойn-го
порядка,
![]() если:
если:
1)
![]() 2)
2)![]()
Решение. 1) Вычислим производную 1-го порядка:
![]()
Далее
![]()
![]()
Установив закономерность, запишем формулу для производной n-го порядка:
![]()
Докажем справедливость этой формулы методом математической индукции.
При
![]() имеем
имеем![]() что совпадает с найденной ранее
производной
что совпадает с найденной ранее
производной![]() Предположим, что наша формула верна при
Предположим, что наша формула верна при![]() т. е.
т. е.![]()
Докажем, что она
верна и для
![]() Вычислим:
Вычислим:
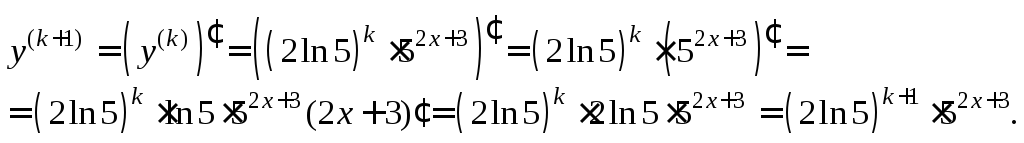
Получили, что
равенство выполняется при
![]() По методу математической индукции
формула будет верна для любого
По методу математической индукции
формула будет верна для любого![]()
2) Вычисляем последовательно:
![]()
![]()
![]()
![]()
Приходим к заключению, что
![]()
Справедливость этой формулы доказывается методом математической индукции.
Пример 3.
Для функции, заданной уравнением
![]() найти производную второго порядка.
найти производную второго порядка.
Решение.
Функция задана в неявном виде.
Дифференцируем обе части равенства
![]() рассматриваяy
как функцию переменной x:
рассматриваяy
как функцию переменной x:
![]()
![]() (17.16)
(17.16)
Выражая
![]() из равенства (17.16), получим:
из равенства (17.16), получим:
![]() (17.17)
(17.17)
Продолжаем дифференцировать по переменной x равенство (17.16):
![]()
![]()
Из последнего
равенства выражаем
![]()
Подставим в эту
формулу найденное выражение (17.17) для
![]() получим:
получим:
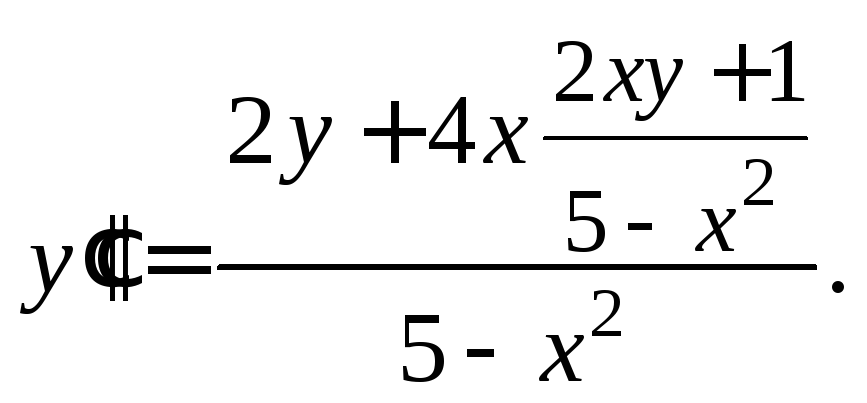
После упрощения
приходим к ответу:

Пример 4.
Вычислить
![]() если
если
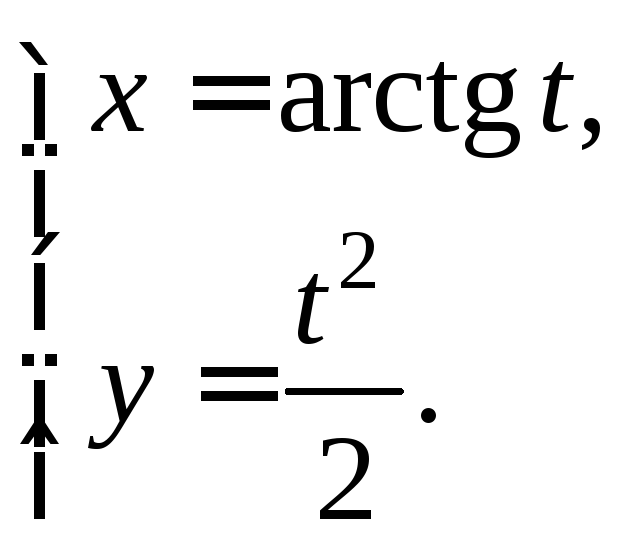
Решение. По формуле (17.6) получаем
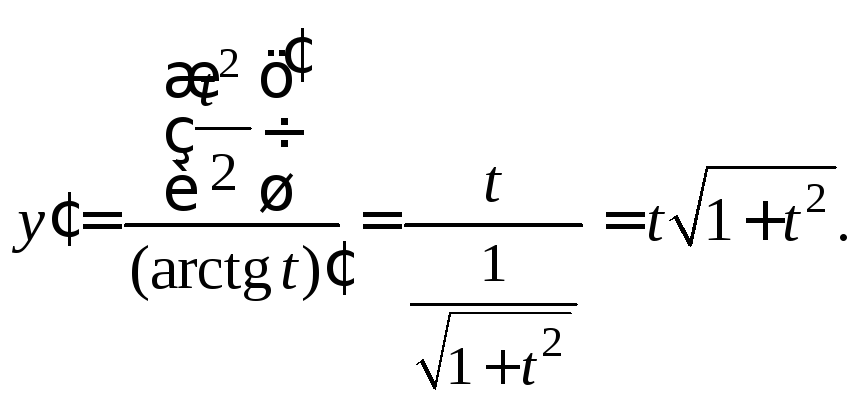
Имеем:
![]()
Для нахождения производной второго порядка снова используем формулу (17.6):

Результат может быть записан в виде
![]() (17.18)
(17.18)
Дифференцируем еще раз:
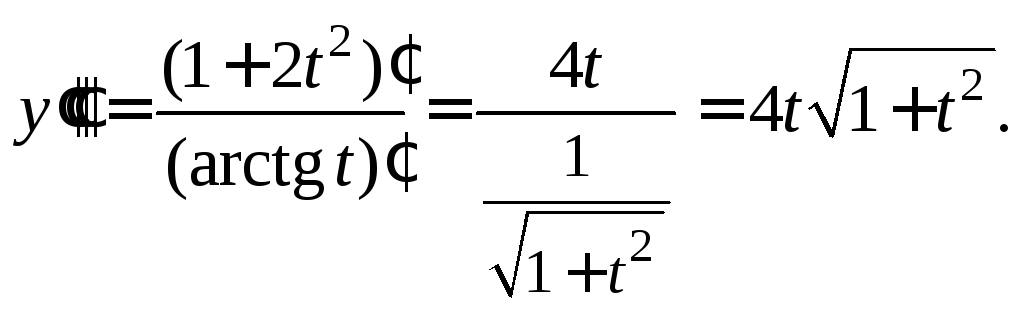
Из первого равенства системы (17.18) можем выразить t через x:
![]()
Подставляем полученное выражение в формулу производной третьего порядка и приходим к ответу:
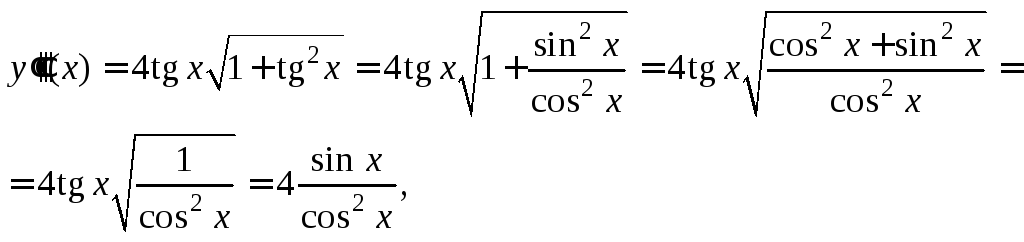
т. е.
![]()
Пример 5.
Найти
![]() для функции
для функции
![]()
Решение.
Согласно формуле (17.15), для дифференциала
3-го порядка справедлива формула
![]()
Последовательно вычисляем производные заданной функции:
![]()
![]()
![]()
Подставив полученное
выражение в формулу
![]() приходим к ответу:
приходим к ответу:
![]()
Задания
