I уровень

1.1. Найдите производную функции, заданной параметрически, возможными способами:

1) 2)

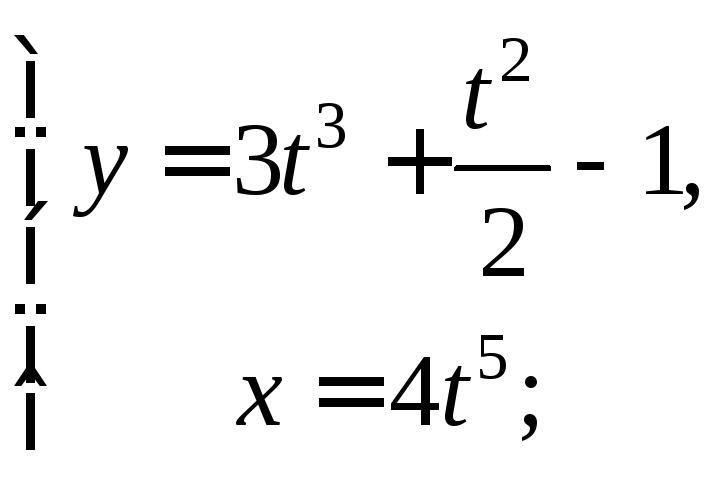3) 4)

1.2. Найдите производную неявно заданной функции возможными способами:

1) 2)

3) 4)

II уровень

2.1. Найдите производную

1) 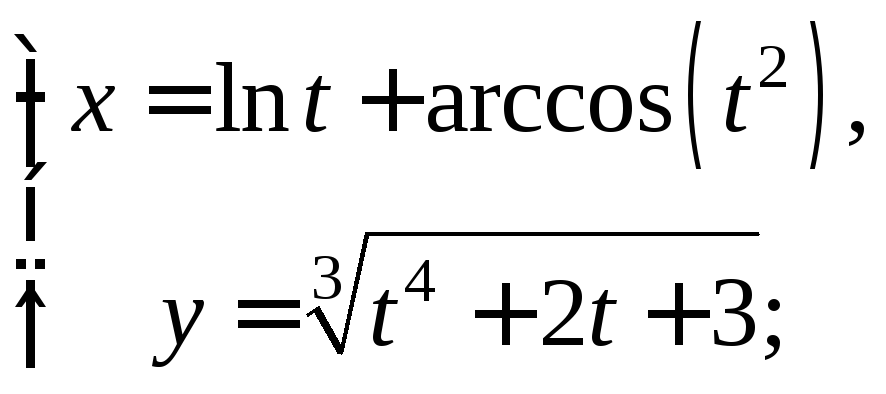2)

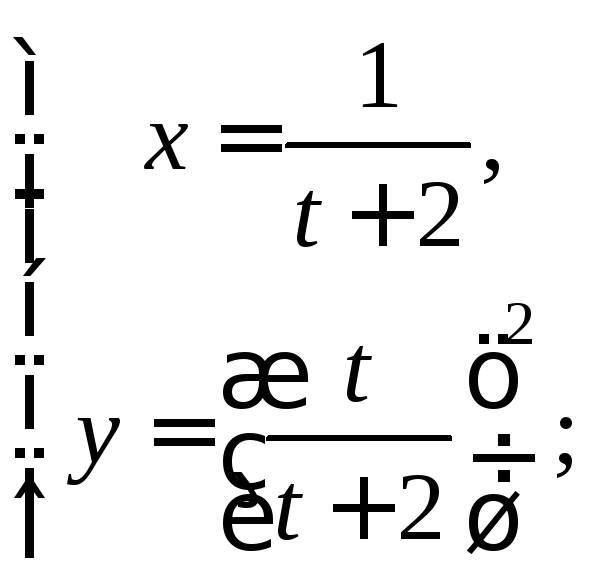3) 4)

2.2. Найдите производную функции, заданной неявно:

1) 2)

3) 4)

5) 6)

2.3. Вычислите производную в точке функции, заданной параметрически:

1) 2)

3) 4)

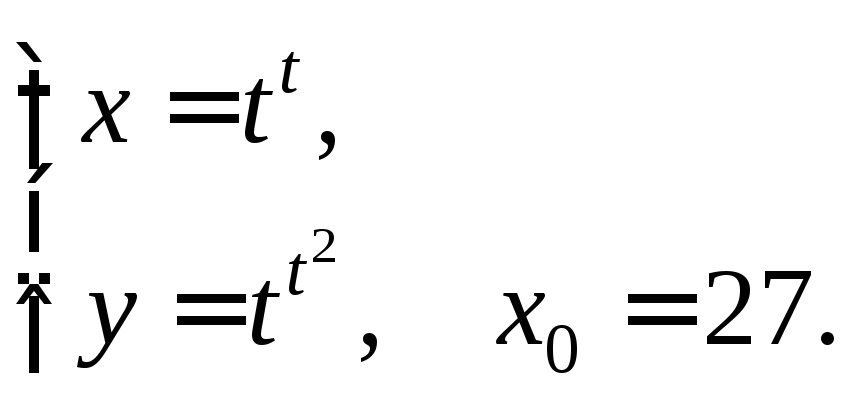
2.4. Вычислите для функцииу, удовлетворяющей указанному уравнению:

1) 2)

3) 4)

III уровень

3.1. Найдите значение производной в точкедля функциизаданной уравнениемесли

3.2. Вычислите для функции, заданной уравнениемесли

3.3. Составьте уравнения касательной и нормали к параболе проведенных в точке

3.4. Запишите уравнение нормали к астроиде в точке, для которой

3.5. Запишите уравнения касательных и нормалей к кривой в точках пересечения ее с осьюOx.

3.6. Найдите уравнения касательной и нормали к кривой в точке (– 2; 3).

17.3. Необходимое и достаточное условия

дифференцируемости функций. Дифференциал

функции

Функция f(x) называется дифференцируемой в точке если ее приращениев этой точке может быть представлено в виде

(17.7)

где (17.8)

Теорема. Для того, чтобы функция f(x) была дифференцируема в точке необходимо и достаточно, чтобы в точкесуществовала производная и в равенстве (17.7) выполнялось условие

Понятие дифференцируемости функции эквивалентно равенству

(17.9)

где – главная часть приращения функции, а для бесконечно малой выполняется (17.8).

Дифференциалом функции f(x) в точке называется главная частьприращения функции. Дифференциал обозначается символоми по определению равен

В частности, для функции получим

Тогда определение дифференциала имеет вид:

(17.10)

Свойства дифференциала

Пусть – дифференцируемые функции на некотором множествеТогда:

1)

2)

3)

4)

5)

6) гдеf(u) – сложная функция, дифференцируемая по переменной (свойство инвариантности дифференциала), т. е.

При достаточно малом значении приращение функции с большой степенью точности можно заменить дифференциалом функции:

или

(17.11)

Формулу (17.11) используют в приближенных вычислениях.

С геометрической точки зрения дифференциал функции dy равен приращению ординаты касательной к кривой в точкекогда аргумент получает приращение

Пример 1. Вычислить при изначение дифференциала функции

Решение. Дифференциал функции вычислим по формуле (17.10). Найдем

Найдем

Подставляя найденные значения в формулу (17.10), получим,

Пример 2. Вычислить дифференциал функции:

1) 2)3)

Решение. 1) Найдем

Подставляя полученное выражение в формулу (17.10), получим:

2) Функция задана параметрически. Выразим из первого уравнения системы переменную t через x:

и подставим во второе уравнение:

которое продифференцируем как сложную функцию:

Производную этой функции, заданной параметрически, можно было вычислять также по формуле (17.6).

Используя формулу (17.10) получим:

3) Функция задана в неявном виде уравнением

Дифференцируем обе части уравнения, считая, что

Выразим

По формуле (17.10), получим:

Пример 3. Вычислить приближенно с помощью дифференциала значение выражения:

1) 2)3)

Решение. 1) Воспользуемся формулой (17.11) для функции приСчитаем, что

Вычислим

Найдем

Тогда:

Таким образом,

2) Будем находить приближенное значение функции в точкепо формуле (17.11). Обозначимоткуда

Найдем значение

Вычислим производную функции

откуда

Подставив найденные значения в формулу (17.11), получим

Таким образом, получим ответ

3) Необходимо найти приближенное значение функции в точке

Представим откуда

Тогда

Поскольку то

Тогда по формуле (17.11) получим:

Итак,

Пример 4. Куб со стороной а = 10 увеличился на 0,05 своего объема. Вычислить приближенно приращение ребра куба.

Решение. Объем куба со стороной a вычисляется по формуле Поэтому первоначальный объем куба равенПо условию приращение объема куба равно 0,05 всего объема, т. е.

Так как то

Дифференциал функции вычисляем по формуле (11.9), т. е.

откуда

Вычислим значение производной для

Теперь находим

Таким образом, ребро куба увеличилось приблизительно на 0,17.

Задания