I уровень

1.1.Вычислите смешанное произведение векторов:

1) 2)3)4)

1.2.Определите ориентацию тройки векторов:

1) 2)

3) 4)

1.3.Вычислите смешанное произведение векторови укажите ориентацию тройки векторов

1)

2)

3)

4) .

II уровень

2.1.Выясните, компланарны ли векторы

1)

2)

3)

4) .

2.2. Установите, образуют ли векторыбазис, если:

1)

2) .

2.3.Вычислите объем параллелепипеда, построенного на векторах

1)

2)

III уровень

3.1.Вычислите объем тетраэдра с вершинами в точкахA(1, 1, 1), B(2, 3,2), C(4, 2, 5) и D(5, 3, 6) и высоту, опущенную на грань ABCиз вершиныD.

3.2.Векторыиобразуют угол 30°,Векторперпендикулярен векторамиЗная, чтовычислите.

3.3.Даны два вектораи. Найдите еди­ничный векторперпендикулярный векторамии направленный так, чтобы упорядоченная тройка векторовбыла правой.

3.4.Упростите:

1) ; 2);

3) ; 4).

3.5.Для тетраэдраSABC, заданного вершинамиS(1, 0, –1), A(1, 2, 1), B(–1, 1, 5) и C(–2, 0, 1), найдите:

1) угол между ребрами ии

2) площадь основания ABC;

3) высоту тетраэдра (из вершины S).

14.5. Цилиндрическая и сферическая

системы координат

Цилиндрические координаты являются обобщением полярных на случай трехмерного пространства.

Рассматривается координатная плоскость xOyс полюсомOи полярной осьюOx. Пусть M– произвольная точка пространства, аM₁– ее проекция на плоскостьxOy.Цилиндрическими координатамиточкиMназываются три числагде– полярные координаты точкиM₁,(рис. 14.4),или

Рис. 14.4

Прямоугольные координаты x,y,zточкиM будут связаны с цилиндрическими формулами:

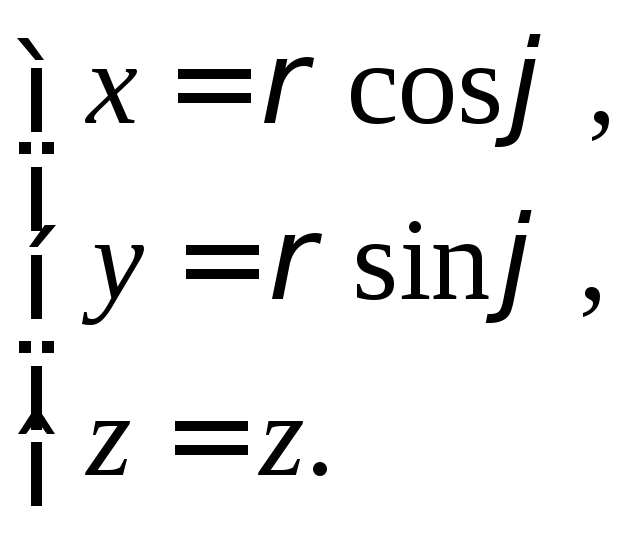(14.12)

Сферическими координатами точки M называются три числа где– полярный угол точкиM₁, а (рис. 14.5), или

Рис. 14.5

Прямоугольные координаты точки Mсвязывают со сферическими формулами:

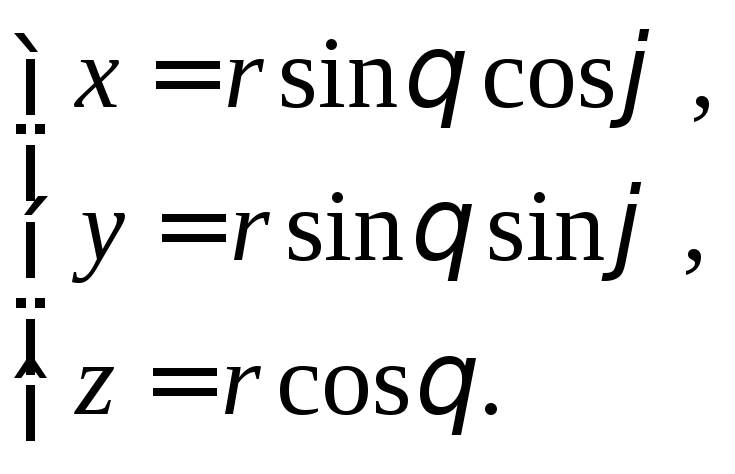(14.13)

Пример 1. Найти цилиндрические координаты по их прямоугольным координатам, если

Решение. Используем рис. 14.4. Исходя из определения цилиндрических координат, имеем:

Точка имеет координатыЗначит,Для нахожденияудобно использоватьс учетом четверти, в которой находится проекцияA₁ точки A на плоскость xOy (рис. 14.6), а именно: I четверти, значит,

Рис. 14.6

Осталось добавить Таким образом, в цилиндрической системе координат.

Рассмотрим точку . Для наглядности изобразим ее проекциюB₁ на плоскость xOy (рис. 14.7).

Рис. 14.7

Очевидно, что остается добавитьТаким образом, в цилиндрической системе координат

Точка имеет в плоскостиxOy проекцию (рис. 14.8), для которой

Находим полярный угол

так как находится вIV четверти (рис. 14.8).

Рис. 14.8

Таким образом, в цилиндрической системе координат получаем

Точка имеет проекцией на плоскостьxOy точку находящуюся вIII четверти (рис. 14.9).

Рис. 14.9

Так как причем

Для нее

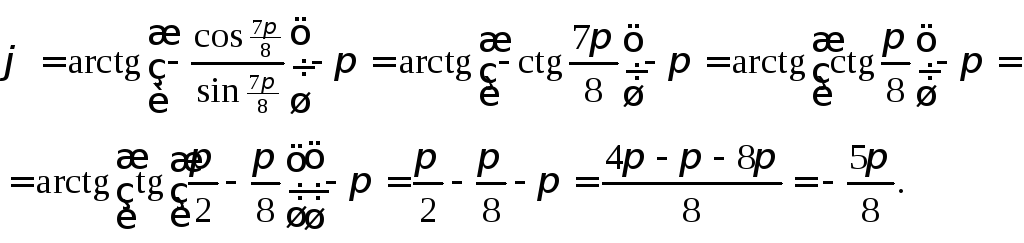
Итак,

Пример 2. Найти сферические координаты точек A(1, 1, 1), B(–4, 8, –1), C(–1, –2, –2) и D(–9, 0, 0).

Решение. Используем рис. 14.5. Сферические координаты точки M(x, y, z) выражаются через декартовы следующим образом:

φ – полярный угол проекции точкиM на плоскости xOy. что позволит для его нахождения использовать формулу

где – единичный вектор осиOz.

Рассмотрим точку A(1, 1, 1) и ее проекцию A₁(1, 1) на плоскость xOy (рис. 14.10).

Рис. 14.10

Для них посколькулежит вI четверти, то илиТаким образом, в сферической системе координат точка.

Для точки B(–4, 8, –1) имеем проек­цияB₁(–4, 8) на плоскость xOy определяется полярным углом (рис. 14.11).

Рис. 14.11

Получаем откудаТаким образом, в сферической системе координат

Прямоугольные координаты точки C(–1, –2, –2) и ее проекции C₁(–1, –2) на плоскость xOy (рис. 14.12) позволяют найти сферические координаты точки C:

Рис. 14.12

Таким образом, в сферической системе координат

Точка D(–9, 0, 0) и ее проекция D₁(–9, 0) на плоскость xOy приводят к сферическим координатам т. е. в сферической системе координат

Пример 3. Найти прямоугольные координаты точек A и B, если цилиндрические координаты точки а сферические координаты точки

Решение. Поскольку точка задана в цилиндрической системе координат, т. е.то прямоугольные координаты находим по формулам (14.12):

Итак, в прямоугольной декартовой системе координат .

Точка задана в сферической системе координат, что значитДля нахождения прямоугольных координат используем формулы (14.13):

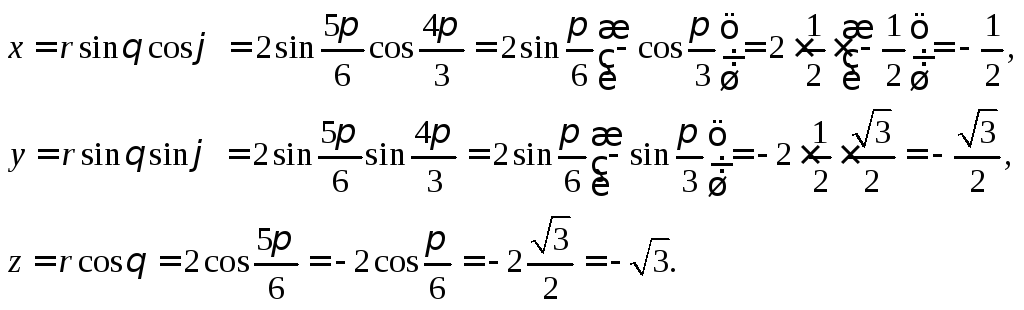
Таким образом, в прямоугольной системе координат

.

Пример 4. Определить фигуры, заданные в цилиндрической системе координат соотношениями:

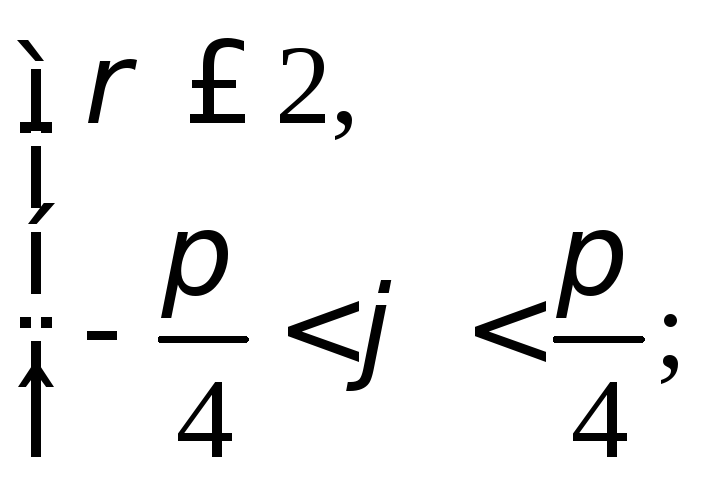1) 2)3)

Решение. 1) Для цилиндрической системы координат гдеx, y – декартовы координаты проекции (при переменном значении ).Условие означает, что еслизначит задан круговой цилиндр.

2) Условие в декартовых координатах означаетПоследнее условие определяет в пространстве внутреннюю область цилиндра с его границей – круговой цилиндрической поверхностью.

Уравнения изадают полуплоскости, которые образуют двугранный угол. Условиеозначает внутреннюю область двугранного угла. Система неравенств определяет пересечение внутренней области двугранного угла и замкнутой внутренней области цилиндра.

3) Заданное условие в декартовых координатах имеет вид:

Условие задает пересечение двух открытых полупространств. Одно представляет внешнюю область кругового цилиндра а второе – часть пространства, ограниченного сверху плоскостью

Пример 5. Фигуры заданы в прямоугольных координатах. Найти уравнения этих фигур в соответствующих цилиндрических координатах:

1) 2)

Решение. 1) Условие в пространстве определяет координатную плоскостьyOz. Используя первую формулу из (14.12), имеем Получили уравнение координатной плоскостиyOz в цилиндрических координатах.

2) Выделяя полный квадрат относительно z, приходим к уравнению Оно задает в пространстве сферу с центром (0, 0, – 1) и радиусом 2.

Пример 6. В прямоугольных координатах известны уравнения фигур:

1) 2)

Написать эти уравнения в сферических координатах.

Решение. 1) Запишем уравнение в видеилиТогда, учитывая, чтоимеем:

2) Поскольку то уравнениепримет вид:

Задания