I уровень

1.1.Даны векторыив некотором базисе. Найдите координаты векторов:

1) 2)3)4)

1.2. Найдите прямоугольные декартовы координаты вектора если известны углыи на

1)

2)

3)

4)

1.3.Заданы векторыиНайдите:

1) 2)

3) координаты вектора 4)

5) 6)

1.4.Найдите значение числаλ, при котором векторыиперпендикулярны.

1.5.Вычислите работу, произведенную силойпри перемещении ее точки приложения из начала в конец вектора

II уровень

2.1.Даны векторыПодберите числатакие, чтобы векторыобразовали замкнутую ломаную.

2.2.Покажите, что векторыобразовывают в пространстве базис и найдите координаты векторав этом базисе:

1)

2)

2.3.Найдите векторколлинеарный векторуобразующий с векторомострый угол и имеющий длину

2.4.Найдите векторобразующий со всеми тремя базисными векторамиравные острые углы, если

2.5.Найдите векторобразующий с ортомугол 60°, с ортом– угол 120°, если

2.6.Вычислите координаты вектора, длина которого равна 8, зная, что с векторомон образует угол 45°, с вектором– угол 60°, с вектором– тупой угол.

2.7.Определите координаты концов отрезка, который точкамиC(2, 0, 2) иD(5, –2, 0) разделен на три равные части.

2.8.Вычислите скалярное произведение векторов:

1) и

2) и

2.9.Найдите угол между векторами

1) и

2) и

2.10. Для векторов инайдите векторудовлетворяющий условиям

III уровень

3.1. Даны три некомпланарных вектора Вычислите значенияλ, при которых векторы компланарны.

3.2.Даны три вершиныA(3, – 4, 7),B(–5, 3, 2) иC(1, 2, –3) параллелограммаABCD. Найдите его четвертую вершинуD.

3.3.Даны вершины треугольникаA(3, –1, 5),B(4, 2, –5) иС(–4, 0, 3). Найдите длину медианы, проведенной из вершиныA.

3.4.Даны вершиныA(1, –1, –3),B(2, 1, –2) иC(–5, 2, –6) треугольникаABC. Вычислите длину биссектрисы его внутреннего угла при вершинеA.

3.5. Треугольник задан координатами своих вершин A(3, –2 1), B(3, 1, 5) и C(4, 0, 3). Вычислите расстояние от начала координат до точки пересечения медиан этого треугольника.

3.6. В вершинах треугольника A(1, –1, 2), B(0, 4, 2) и C(2, –1, 1)сосредоточены массы 1, 2, 3 соответственно. Найдите координаты центра масс этой системы.

У к а з а н и е. Из функции известно, что для пары масс m₁ и m₂, сосредоточенных в точках A и B, центр находится в точке, делящей отрезок AB в отношении гдеи– расстояние от соответствующих точек до их центра.

3.7.Даны два вектора:иНайдите векторкомпланарный векторамиперпендикулярный векторуравный ему по длине и образующий с векторомтупой угол.

3.8.Векторыимеют равные длины и образуют попарно равные углы. Найдите координаты вектораесли

3.9.Выразите координаты векторав базисечерез координаты в базисеи наоборот, если

14.3. Векторное произведение

Векторным произведениемдвух векторовиназывается вектор, удовлетворяющий следующим условиям:

1)

2)

3) тройка векторов – правая.

Векторное произведение обозначают также

Если хотя бы один из векторов илинулевой, то

Геометрический смыслвекторного произведениясостоит в том, что длина этого вектора численно равна площади параллелограмма, который построен на векторахи, приведенных к общему началу,

Физический смыслвекторного произведения состоит в том, что моментсилыприложенной к точкеAотносительно точкиO, есть векторное произведение векторовит. е.

Свойства векторного произведения

1.

2.

3.

4. притогда и только тогда, когда векторыиколлинеарны.

Если векторы изаданы в ортонормированном базисе иито

Последнюю формулу удобно записать в виде формального определителя третьего порядка

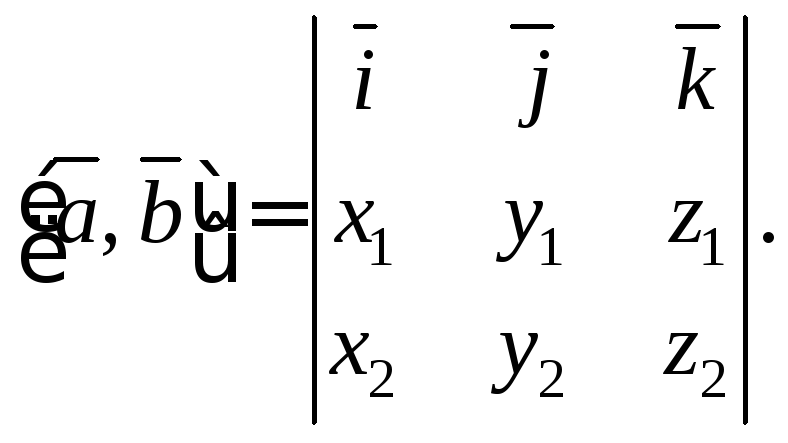
Пример 1. Пусть Найти:

1) 2)3)

Решение. 1) По определению векторного произведения векторов иего длина

2) Используя алгебраические свойства векторного произведения, имеем:

Значит,

3) Используя свойства векторного произведения и условие задачи, получим:

Пример 2. Упростить выражение:

1)

2)

Решение. Воспользуемся равенствами

Тогда имеем:

1)

2)

Пример 3. Вычислить площадь параллелограмма, диагоналями которого служат векторы игде

Решение. Используем известную из планиметрии формулу площади параллелограмма и геометрический смысл векторного произведения:

где

Тогда по свойствам векторного произведения получим:

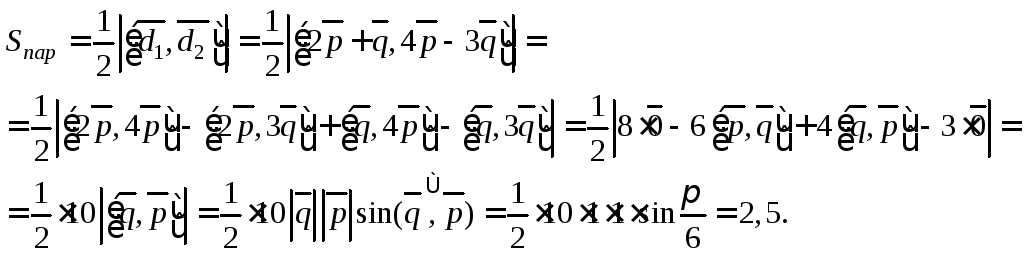
Пример 4. Вычислить площадь треугольника ABC и его высоту, опущенную из вершины A к стороне BC, если A(1, 1, 1), B(4, 2, –1), C(2, 3, 0).

Решение. Используем тот факт, что где– площадь параллелограмма, построенного на векторахи. Так какнайдем сначала

Вычисляем векторное произведение в координатной форме:

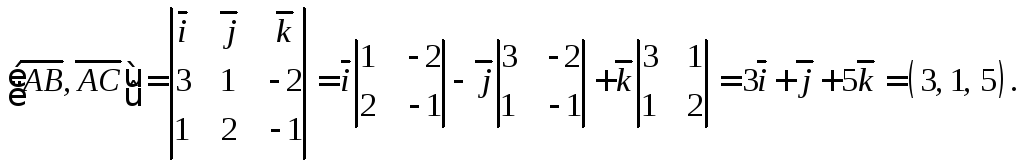
Тогда

Значит,

Для нахождения высоты h треугольника ABC воспользуемся формулой Тогдаздесь

Значит

Пример 5. Даны три силы: приложенные к точкеA(–1, 4, 2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки O(2, 3, –1).

Решение. Пусть сила – равнодействующая силТогдаЗначит моментэтой силы равен

Вычисляем Для нахождения направляющих косинусов используем формулы (14.9):

Задания