II уровень

2.1.В тетраэдреABCDизвестны векторыПредставьте векторв виде линейной комбинации векторовеслиO– точка пересечения медиан треугольникаABC.

2.2.Докажите, что если векторыинеколлинеарны, то векторкомпланарен с векторамиитогда и только тогда, когда имеет место разложение

2.3. Найдите проекцию вектора на направление вектораесли

2.4.Известно, чтоиНайдите

2.5.При каком значенииαвекторыиперпендикулярны, если

III уровень

3.1.Векторыиобразуют угол 120°. Найдите числоkиз условий, чтои векторперпендикулярен вектору

3.2.Пустьи– единичные неколлинеарные векторы. Вычислитеесли

3.3.Определите, при каком значенииmвекторыиперпендикулярны, еслии

14.2. Линейная зависимость векторов. Действия

над векторами в координатной форме

Векторы называютсялинейно-независимыми, если равенствосправедливо тогда и только тогда,когда В противном случае эти векторы называютсялинейно-зависимыми. Для того чтобы векторы былилинейно-зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.

Упорядоченная тройка ненулевых линейно-неза­висимых векторов образуетбазисв трехмерном пространстве. Это значит, что любой векторэтого пространства единственным образом может быть представлен в виде

где – координаты векторав базисеЗаписывают:

В физическом пространстве линейная независимость векторов равносильна их некомпланарности. Таким образом, любая тройка ненулевых некомпланарных векторов, взятых в определенном порядке, образует базис этого пространства.

Пусть задана тройка некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот векторадо направления векторанаблюдаемый с конца векторасовершается против часовой стрелки, то тройка векторовназываетсяправой. В противном случае –левой. Всюду далее будем рассматривать правые тройки базисных векторов.

Совокупность базисных векторов и их общего начала образует, говорят, аффинную систему координат в пространстве. Координаты векторов в таком случае называютаффинными.

Если даны два вектора ив некотором базисе, тотогда и только тогда, когда

(14.2)

(14.3)

В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой системой координат. Если добавить, кроме того, условие нормированности базисных векторов (или их единичную длину), то получимортонормированныйбазис, который обозначаютТаким образом,Прямоугольные декартовы координаты вектораявляется его проекциями на векторысоответственно. В частности, если точкаMимеет прямоугольные декартовы координатыx,y,zв системе координат с началом в точкеO(0, 0, 0) и базисом, то радиус-векторравен

Если ито

а длина этого вектора может быть найдена по формуле

Линейные операции для векторов и в координатной форме и их скалярное произведение вычисляются по формулам:

(14.4)

(14.5)

(14.6)

(14.7)

(14.8)

Направляющими косинусамивектораназываются величиныгде– углы, которые образует векторсоответственно с осямиOx,Oy,Oz. Их вычисляют по формулам:

(14.9)

Если – единичный вектор, то.

Координаты точки C, делящей отрезокABв отношенииможно найти по формулам:

(14.10)

Пример 1. Даны векторы в некотором базисе. Найти координаты векторав этом базисе.

Решение. Определим координаты вектора следуя правилам действий над векторами в координатной форме, т. е.

В дальнейшем, если не оговорено противное, все координаты считаются заданными в ортонормированном базисе.

Пример 2. Вычислить проекцию вектора на направление вектора

Решение.

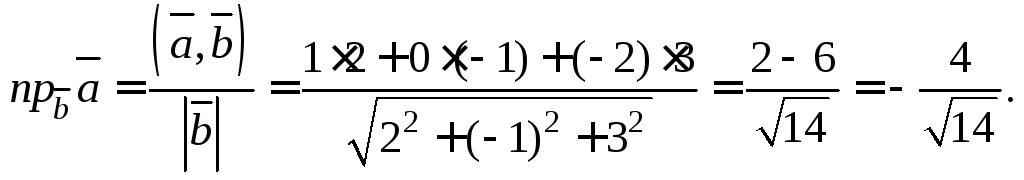
Пример 3. Найти направляющие косинусы вектора

Решение. Используем формулы (14.9):

Пример 4. Найти прямоугольные декартовы координаты вектора если

Решение. Пусть тогда

Итак,

Пример 5. Даны векторы иВычислить:

1) 2)3)4)

5) 6)7)

Решение. 1) Используем формулу (14.6):

2) Сначала вычислим координаты векторов ииспользуя формулы (14.4) и (14.5):

Тогда согласно формуле (14.6) получим:

3) Найдем координаты суммы векторов:

Далее, используя формулу скалярного квадрата и формулу (14.7) длины вектора, получим:

4) Вычислим координаты вектора используя формулы (14.4) и (14.5):

Тогда по формуле (14.7) получим:

5) По формуле (14.1) получим:

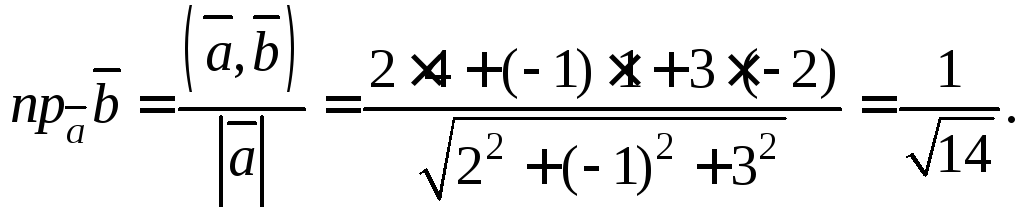
6) Используя формулы (14.1), (14.4)–(14.7), получим:

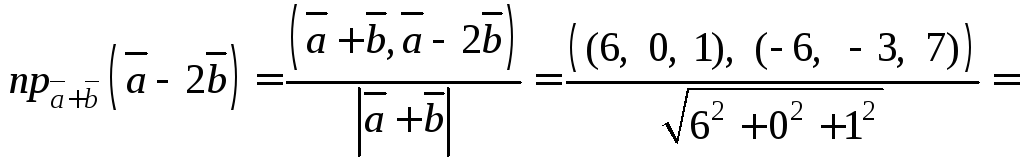
7) Вектор – это единичный вектор направления вектора:

Пример 6. Вектор перпендикулярен векторамии удовлетворяет условиюгдеНайти координаты вектора

Решение. Пусть По условиючто влечетт. е.Аналогично из условияполучаемНаконец, изимеем

Получили систему уравнений

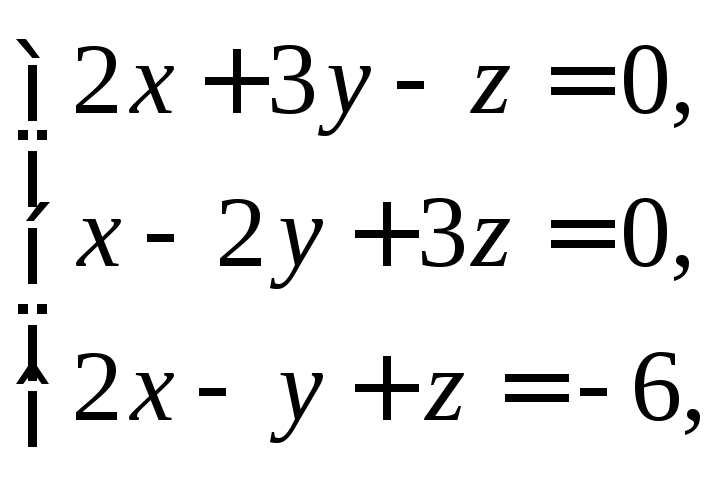
Решая которую, придем к ответу:

т. е.

Пример 7. Даны векторы иНайти косинус угла между векторамиидля которых

Решение. Выразим векторы ичерезиИз равенства получимТогда, используяполучим:

т. е.

Далее находим координаты вектора

Поскольку то

Используя формулу (14.8), находим:

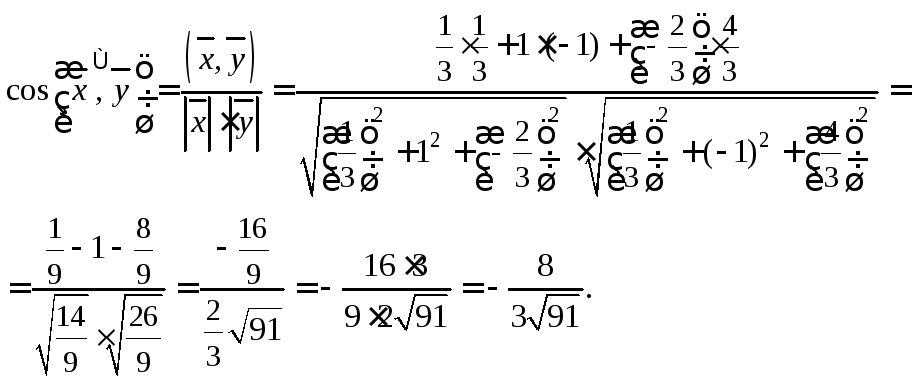
Пример 8. Луч образует с векторами иуглы соответственноиа с вектором– тупой угол. Найти этот угол.

Решение. Рассмотрим единичный вектор сонаправленный с заданным лучом. Он определяется направляющими косинусами, т. е.. Так както имеем илиИз последнего равенства имеемПо условиюγ – тупой угол. Значит, т. е.

Таким образом, искомый угол равен

Пример 9. Показать, что векторы иобразуют базис, и найти координаты векторав этом базисе.

Решение. 1-й способ. В трехмерном пространстве базис образуют любые три линейно-независимых вектора с ненулевой длиной. Определим, будут ли три заданные вектора линейно-независимыми. Для этого составим их линейную комбинацию с коэффициентами и приравняем кт. е. рассмотрим:

Если окажется, что при этом то система этих векторов линейно-независима, а значит, они образуют базис.

Векторному равенству в координатной форме соответствует следующее условие:

Из определения равенства двух векторов имеем систему

решая которую, получим

Найдем в этом базисе координаты вектора

Так как то в координатной форме

что приводит к системе линейных уравнений

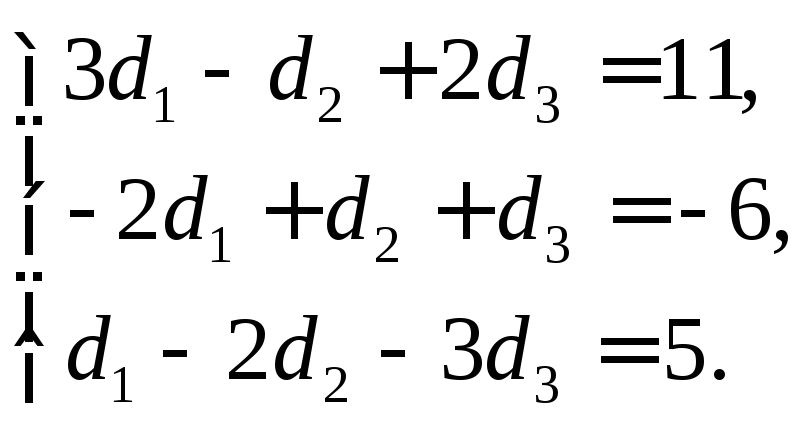
Решая последнюю систему каким-либо методом, получим Это значит что в базисевекторимеет координаты:

2-й способ. Векторы образуют базис пространства, если они некомпланарны. Это равносильно тому, что их смешанное произведение не равно 0, т. е. (в координатной форме)

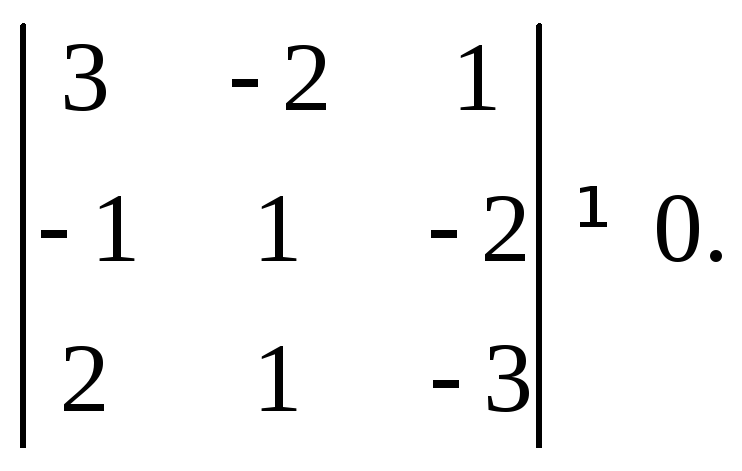
Вычисление последнего определителя показывает, что он не нулевой. Таким образом, векторы образуют базис. Найти координаты векторав этом базисе можно, как в 1-м способе.

Пример 10. Векторы ине коллинеарны. Найти, при каком векторы ибудут коллинеарны.

Решение. Если то существует такое числочтот. е.

откуда

Векторы ине коллинеарны, поэтому

Решая эту систему, находим иилиТаким образом, приКак легко видеть, векторыпротивоположны, т. е.

Задания