I уровень

1.1.Даны векторыитакие, чтоВычислите:

1) 2)3)

1.2.Для векторовинайдите:

1) 2)3)

1.3.Вычислите площадь параллелограмма, построенного на векторахи.

II уровень

2.1.Докажите, чтои выясните гео­метрический смысл этого тождества.

2.2.Какому условию должны удовлетворять векторыичтобы векторыибыли коллинеарными?

2.3.Вычислите площадь треугольника, построенного на векторахи

2.4. Выразите через векторыи единичный векторперпендикулярный векторамии такой, что:

1) тройка векторов – правая;

2) тройка векторов – левая.

2.5.Вычислите площадь треугольника с вершинами в точкахA(1, 1, 1),B(2, 3, 4),C(3, 4,2).

2.6.Силаприложена к точкеA(4, 2, –3). Вычислите величинумоментаэтой силы относительно точкиO(2, 4, 0).

III уровень

3.1.Вычислите длины диагоналей и площадь параллелограмма, построенного на векторахиДокажите, что этот параллелограмм является прямоугольником.

3.2.Найдите составляющую вектораперпендикулярную плоскости векторови

3.3.Найдите синус угла между диагоналями параллелограмма, построенного на векторахи

3.4.Силаприложена к точкеB(2, –3, 4) и перпендикулярна осиOx. Моментэтой силы относительно точкиA(4, 0, –2) равенНайдите

3.5.Докажите, что для векторакоторый называется двойным векторным произведением, справедливо отношение

3.6.Найдитеесли

У к а з а н и е. Можно воспользоваться формулой из предыдущей задачи 3.5.

14.4. Смешанное произведение векторов

Смешанным произведением трех векторовиназывается число, определяемое соотношением

Если хотя бы один из векторов – нулевой, то их смешанное произведение равно нулю.

Геометрический смысл смешанного произведения векторов состоит в том, что его абсолютное значение равно объемуVпараллелепипеда, построенного на векторахприведенных к общему началу:

Свойства смешанного произведения

1.

2.

3. , где

4. притогда и только тогда, когда– компланарные векторы;

5. векторы образуют базис в трехмерном пространстве при условии

6. если то векторыобразуют правую тройку; если– левую.

В случае, когда векторы заданы в ортонормиро­ванномбазисе координатамииих смешанное произведение может быть найдено по формуле

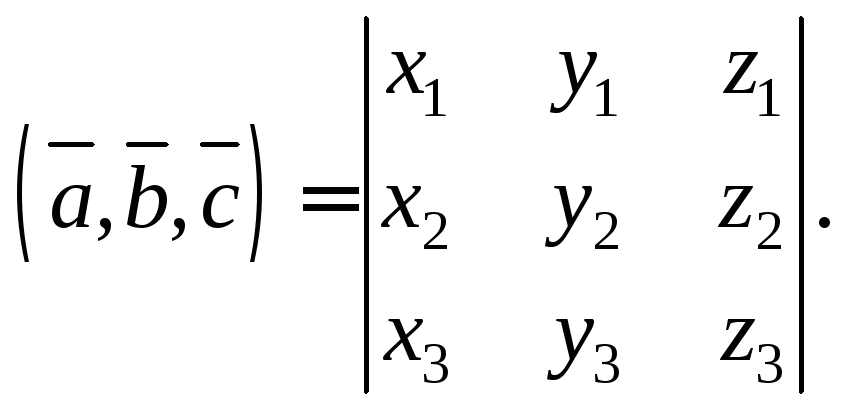(14.11)

Пример 1. Векторы образуют правую тройку, взаимно перпендикулярны иВычислить их смешанное произведение.

Решение. По определению . Векторобразует сиправую тройку, причемЗначит,Кроме того,Тогда

Пример 2. Для векторов инайти объем параллелепипеда, построенного на векторахприведенных к общему началу, и определить ориентацию этой тройки векторов.

Решение. Используем формулу (4.11) для вычисления смешанного произведения в координатной форме:

Поскольку получили отрицательное значение, то тройка векторов является левой, а объем параллелепипеда равен модулю смешанного произведения, т. е.

Пример 3. Доказать, что точки A(1, 2, –1), B(0, 1, 5), C(–1, 2, 1) и D(2, 1, 3) лежат в одной плоскости.

Решение. Рассмотрим три вектора:

Вычисляем их смешанное произведение:

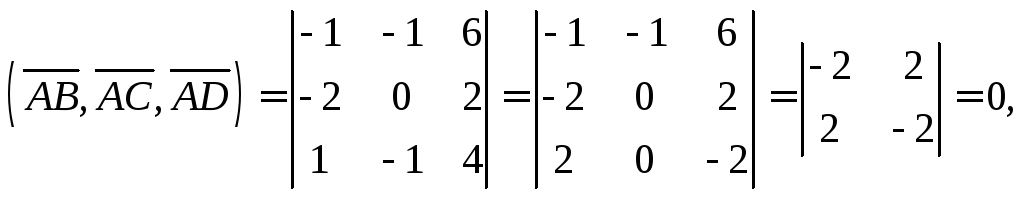
Поскольку оно равно нулю, то это значит, что векторы – компланарны. Они лежат в одной плоскости, так как имеют общее начало. Таким образом, точкиA, B, C и D лежат в одной плоскости.

Пример 4. Вычислить объем тетраэдра OABC, если

Решение. Используем формулу

где – объем параллелепипеда, построенного на векторахОбъем параллелепипеда вычисляется через смешанное произведение

Поскольку

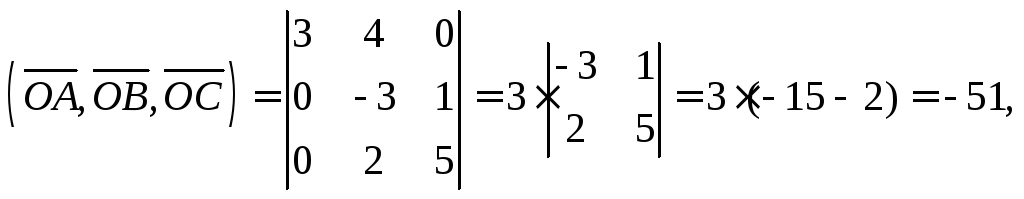
то

Пример 5. Вершины треугольника расположены в точках A(1, 1, 1), B(2, 3, 2) и C(4, 2, 5). Найти расстояние от точки D(5, 3, 6) до плоскости

Решение. Убедимся, что точка D не лежит в одной плоскости с точками A, B и C, для чего найдем смешанное произведение векторов . Если оно будет не нулевым, то тем самым будет доказано, что векторыне являются компланарными, а значит, точкиA, B, C, D не лежат в одной плоскости.

Так как то смешанное произведение равно

Значит,

Поскольку расстояние h от точки D до плоскости численно равно высоте параллелепипеда, опущенной из вершиныD на основание, в котором лежит то из формулынаходим

Найдем Поскольку

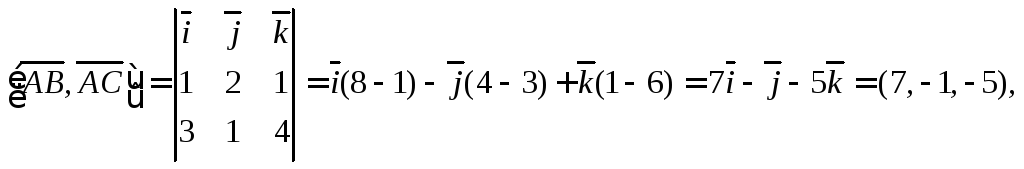
то

Таким образом, т. е. искомое расстояние равно

Пример 6. Доказать, что векторы компланарны, если.

Решение. Умножим скалярно данное равенство на вектор

Так как тоили векторыкомпланарны.

Доказанное можно обобщить на случай, когда задано равенство где– числа, среди которых, по крайней мере, есть одно ненулевое.

Задания