14. Векторная алгебра

14.1. Векторы в пространстве: линейные операции

над векторами в геометрической форме,

проекция вектора на ось

Как и на плоскости (см. § 8.1), векторы в пространстве определяются как направленные отрезки, для которых вводятся операции сложения (правило треугольника, параллелограмма для двух векторов и правило ломаной для nвекторов) и умножения на число. Эти операции обладают теми же свойствами, что и операции на плоскости.

Векторы называются компланарными, если они лежат в параллельных плоскостях (или в одной плоскости). Для трех некомпланарных векторовсправедливосложение по правилу параллелепипеда:

где – диагональ параллелепипеда, построенного на векторахс общим началом, с тем же началом (рис. 14.1).

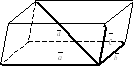
Рис. 14.1

Геометрической проекцией вектора на осьlназывается вектор, гдеи– основания перпендикуляров, опущенных на ось из точекAиBсоответственно (рис. 14.2).

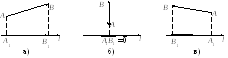
Рис. 14.2

Если тоявляется геометрической проекцией (или составляющей) векторана осьlи обозначается

Алгебраической проекцией(простопроекцией) векторана осьl называется числокоторое определяется следующим образом:

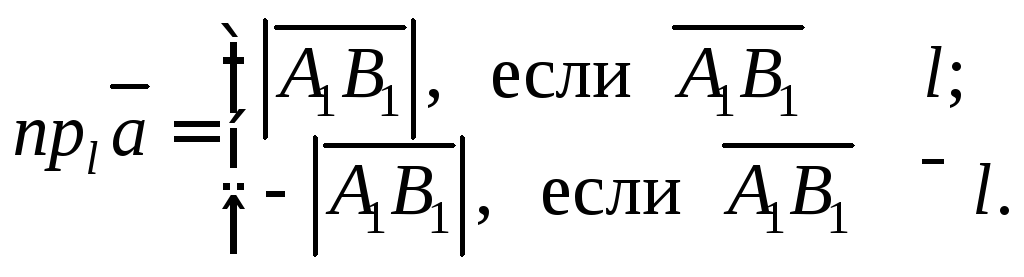
Запись обозначает проекцию векторана направление векторат. е. на ось, определяемую ортом

Свойства проекции вектора на ось

1.

2.

3.

4.

Скалярное произведение двух векторов в пространстве определяется аналогично случаю на плоскости:

Формула скалярного квадрата:

Справедлива формула, связывающая скалярное произведение векторов и проекции этих векторов:

(14.1)

Пример 1. Дана треугольная призма (рис. 14.3). Разложить векторпо векторами

Решение. По правилу треугольника имеем:

Складывая левые и правые части этих векторных равенств, получаем:

Так как ито и, следовательно,

Рис. 14.3

Пример 2. При соблюдении каких условий ненулевые векторы иудовлетворяют условию?

Решение. Так как неравенство связывает неотрицательные числовые величины, возведем в квадрат, что не изменит его смысла:

Перейдя к скалярному квадрату и воспользовавшись алгебраическими свойствами скалярного произведения, получим:

откуда

Получаем:

т. е.

Очевидно, последнее условие выполняется при т. е. при

Таким образом, векторы или сонаправлены или образуют острый угол.

Пример 3. Вычислить иеслиа векторыиобразуют с осьюl соответственно углы в 120° и 45°.

Решение. Согласно свойствам проекции, имеем:

Тогда получаем:

Пример 4. Найти проекцию вектора на направление вектораесли

Решение. Используем свойства проекции:

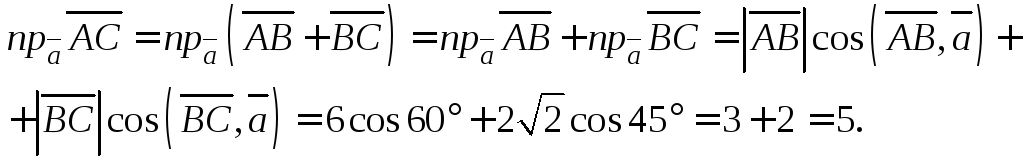
Пример 5. Вычислить длины диагоналей параллелограмма, построенного на векторах иесли

Решение. Пусть и. Тогдаипредставля­ют длины диагоналей параллелограмма, построенного на векторахи

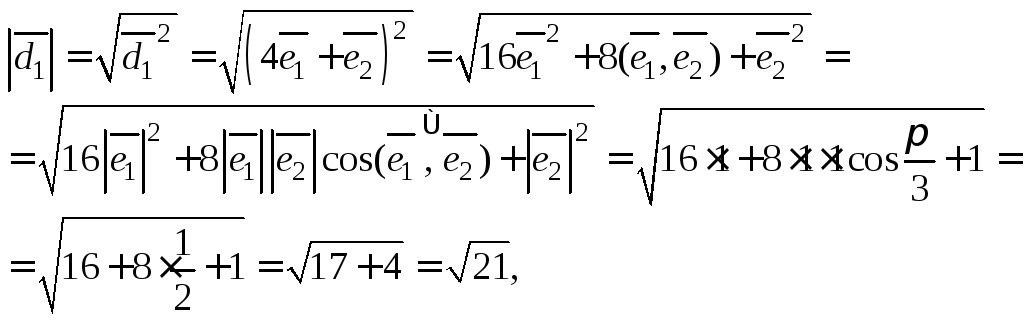
Пример 6. Найти угол между векторами иесли

Решение. Обозначим угол между векторами φ, тогда

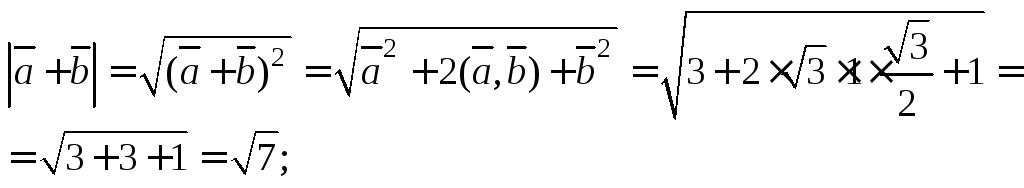
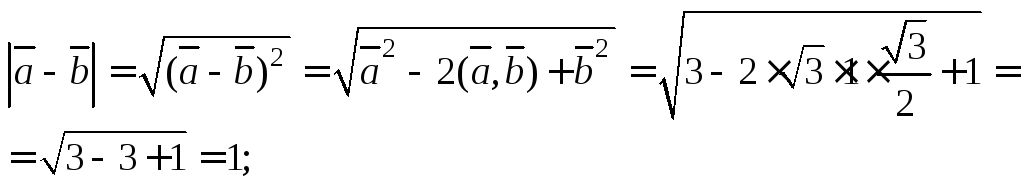
Тогда

Задания

I уровень

1.1.Дан тетраэдрABCD. Найдите сумму векторов:

1) 2)3)

1.2.Дан параллелепипедУкажите, какие из следующих трех векторов компланарны:

1) 2)

3) 4)

1.3.Назовите по три упорядоченных пары вершин тетраэдраABCD, задающие компланарные и некомпланарные векторы.

1.4.Найдитеесли:

1) 2)

3) 4)5)

1.5.Найдите скалярное произведение векторов и, если:

1) 2)

3)

4)

1.6.Найдитеесли известно, чтоа длина