
- •6. Показательные и логарифмические
- •6.1. Показательная функция, гиперболические
- •I уровень
- •II уровень
- •III уровень
- •6.2. Понятие логарифма и его свойства
- •I уровень
- •II уровень
- •III уровень
- •6.3. Логарифмическая функция
- •I уровень
- •II уровень
- •III уровень
- •6.4. Показательные уравнения,
- •I уровень
- •II уровень
- •III уровень
- •6.5. Логарифмические уравнения
- •I уровень
- •II уровень
- •III уровень
- •6.6. Показательные неравенства
- •I уровень
- •II уровень
- •III уровень
- •6.7. Логарифмические неравенства
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1. Определите, для каких значений неизвестного выполняется неравенство:
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
11)
![]() 12)
12)![]()
1.2. Определите, принадлежит ли х = –2 множеству решений неравенства:
1)
![]() 2)
2)![]()
3) ![]() 4)
4)
![]()
1.3. Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
11)
![]() 12)
12)![]()
13)
![]() 14)
14)![]()
15)
![]() 16)
16)![]()
17)
![]() 18)
18)![]()
19)
![]() 20)
20)![]()
21) ![]() 22)
22)
![]()
23)
![]() 24)
24)![]()
25)
![]() 26)
26)![]()
27)
![]() 28)
28)![]()
29) ![]() 30)
30)
![]()
31)
![]() 32)
32)![]()
1.4. Решите неравенство графически:
1)
![]() 2)
2)![]() 3)
3)![]()
II уровень
2.1. Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
11)
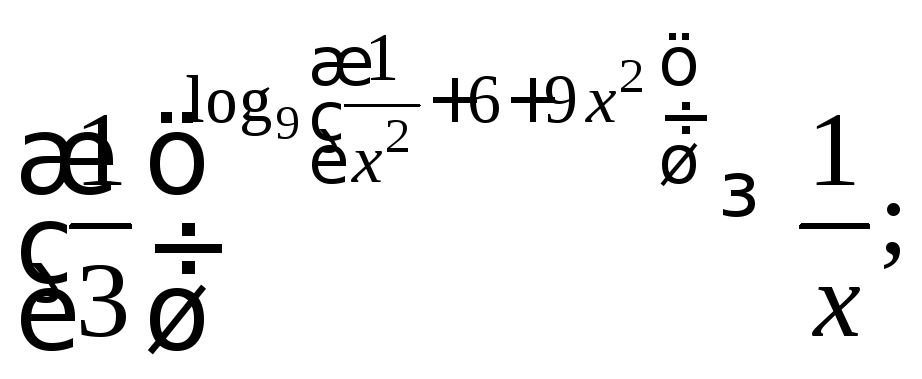 12)
12)![]()
13)
![]() 14)
14)![]()
III уровень
3.1. Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
11)
![]() 12)
12)![]()
3.2. Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)
5)
![]() 6)
6)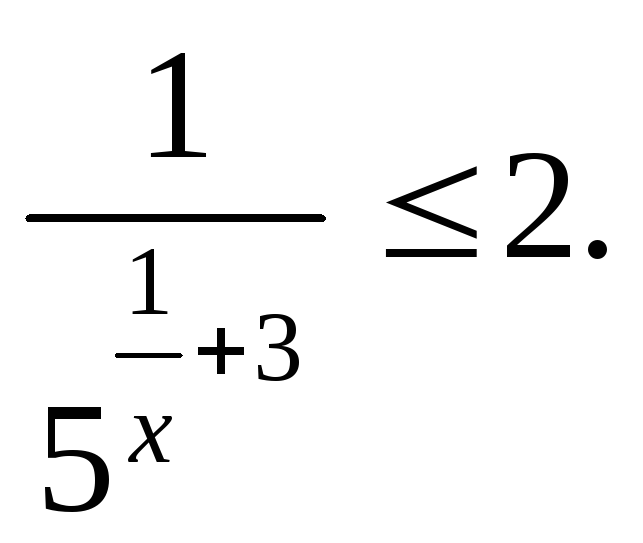
6.7. Логарифмические неравенства
Логарифмическим неравенством называется такое неравенство, в котором неизвестная величина содержится или под знаком логарифма, или в его основании.
Особенностью решения логарифмических неравенств является учет ОДЗ входящих в него логарифмов. В отличие от логарифмических уравнений, условия, определяющие ОДЗ, целесообразно записывать вместе с решением в одной системе, так как в ходе решения некоторые условия на ОДЗ учитываются сразу. Необходимо внимательно следить за величиной основания логарифма, так как при положительном основании логарифма, которое меньше единицы, знак неравенства меняется на противоположный.
Типы неравенств и способы их решения
Всюду далее f(x), g(x), h(x) – некоторые выражения с переменной.
I тип: неравенство вида
![]() (6.16)
(6.16)
где a > 0.
1. Если 0 < a < 1, то неравенство (6.16) равносильно системе
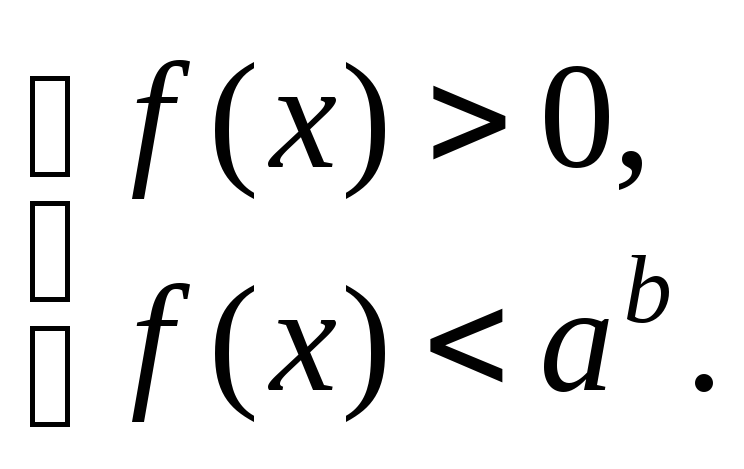 (6.17)
(6.17)
2. Если a > 1, то неравенство (6.16) равносильно системе
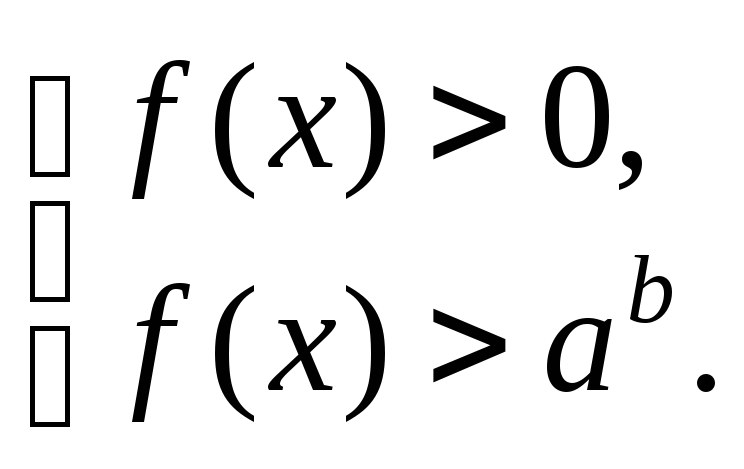
Заметим,
что в этом случае первое неравенство
системы (6.17)
можно не решать, так как во втором
неравенстве ![]()
![]() (6.18)
(6.18)
Решение неравенства (6.18) сводится к решению совокупности двух систем:
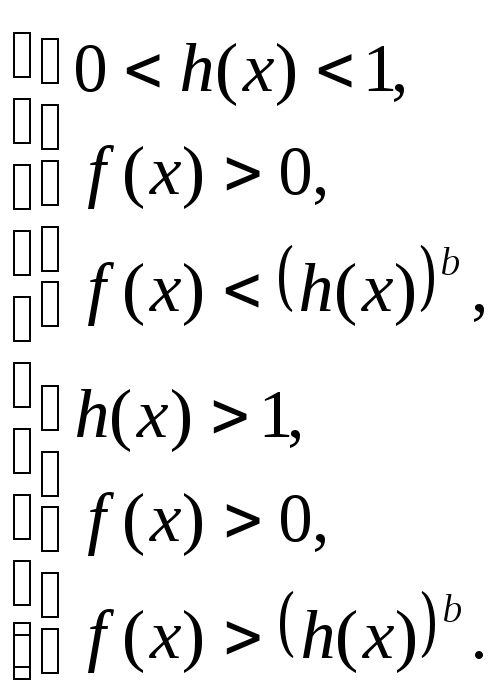
Неравенство f(x) > 0 во второй системе можно не решать, так как оно справедливо при выполнении двух других неравенств этой системы.
II тип: неравенство вида
![]() (6.19)
(6.19)
1. Если 0 < a < 1, то неравенство (6.19) равносильно системе
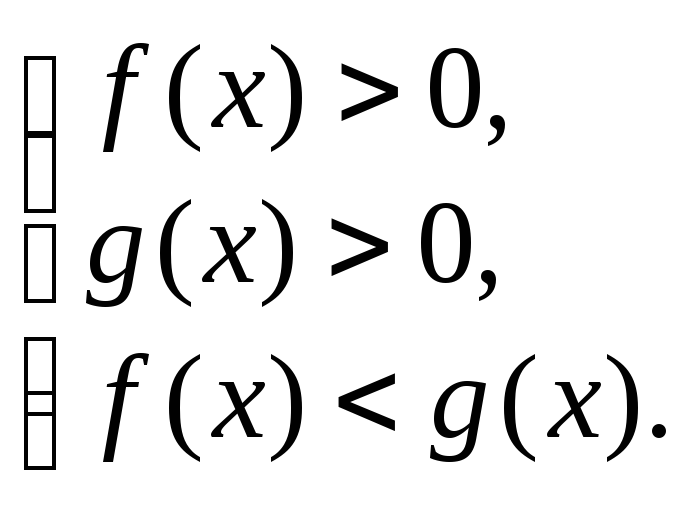 (6.20)
(6.20)
Неравенство g(x) > 0 в системе (6.20) можно не решать, так как оно выполняется при условии выполнения двух других неравенств этой системы.
2. Если
![]() то неравенство (6.19) равносильно системе
то неравенство (6.19) равносильно системе
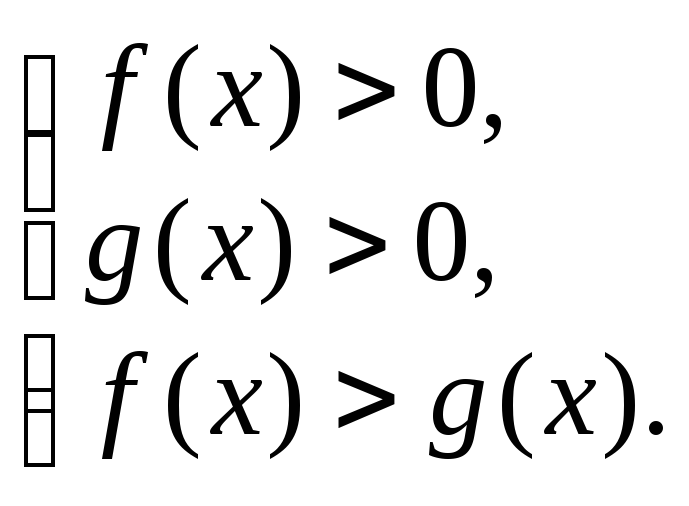 (6.21)
(6.21)
Неравенство ![]() в системе (6.21) можно не решать.
в системе (6.21) можно не решать.
![]() (6.22)
(6.22)
Поскольку в основании содержится переменная величина, то в общем случае решение неравенства (6.22) зависит от величины основания по сравнению с числом 1. Поэтому решаем совокупность двух систем:
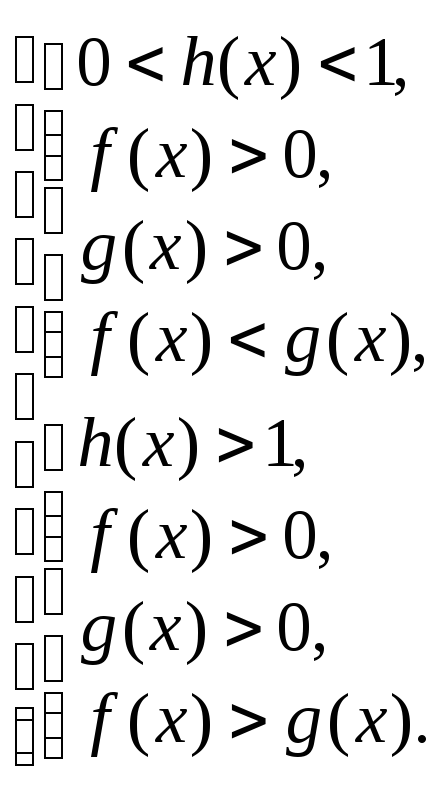
III тип: неравенство вида
![]() (6.23)
(6.23)
где F
– некоторое выражение относительно
![]()
Необходимо заменить
![]() и решить неравенствоF(y)
> 0. Полученные в качестве решения
последнего неравенства промежутки
записывают в виде неравенств относительно
y,
а затем возвращаются к старой переменной.
и решить неравенствоF(y)
> 0. Полученные в качестве решения
последнего неравенства промежутки
записывают в виде неравенств относительно
y,
а затем возвращаются к старой переменной.
Аналогично решают неравенства I – III типов, в которых вместо знака > использованы знаки , <, .
Пример 1.
Решить неравенство ![]()
Решение. Имеем неравенство I типа. Так как основание логарифма меньше числа 1, то решение неравенства сводится к решению системы

![]()
Используем далее метод интервалов (рис. 6.13).

Рис. 6.13
Получаем ответ: ![]()
Пример 2.
Решить неравенство ![]()
Решение. Данное неравенство относится к I типу. Поэтому решаем совокупность двух систем
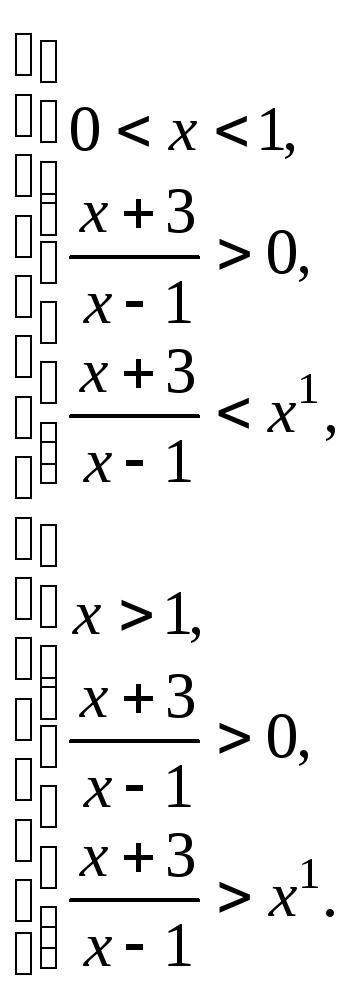
Первая система решений не имеет. Решаем вторую систему

Второе неравенство этой системы не решаем, так как оно справедливо, если выполняется последнее неравенство. Получаем:

Используем метод интервалов (рис. 6.14).

Рис. 6.14
Получаем ответ: ![]()
Пример 3.
Решить неравенство ![]()
Решение. Это неравенство II типа, причем основание логарифма больше числа 1. Поэтому решаем систему
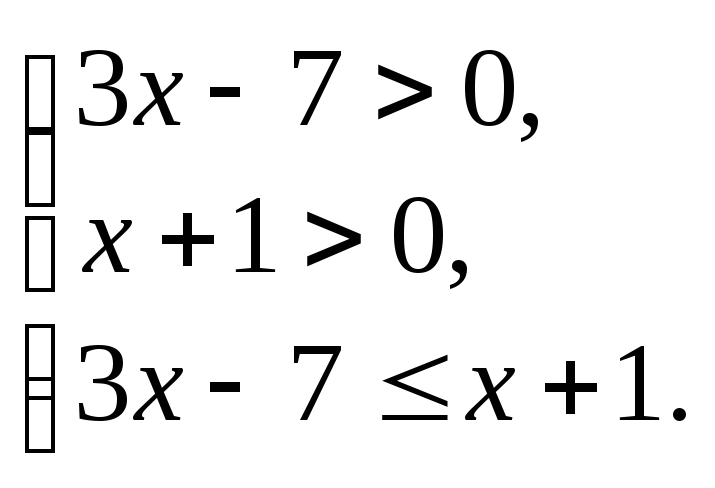
Получаем 
Подводя итог,
приходим к ответу: ![]()
Пример 4.
Решить неравенство ![]()
Решение. Имеем неравенство III типа.
Заменяем ![]() и решаем кубическое неравенство
и решаем кубическое неравенство
![]()
Разлагаем левую часть неравенства на множители:
![]()
![]()
Используем далее метод интервалов (рис. 6.15).

Рис. 6.15
Получили решение
![]() Записываем его в виде:
Записываем его в виде:
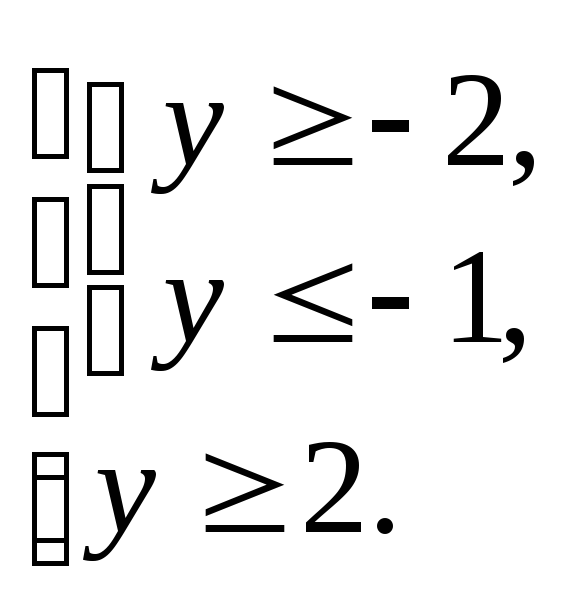
Возвращаемся к неизвестной x и с учетом ОДЗ заданного неравенства имеем:

Получаем ответ: ![]()
Задания
