I уровень

1.1. Решите уравнение:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13)

II уровень

2.1. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

III уровень

3.1. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

3.2. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

6.6. Показательные неравенства

Показательным неравенством называется неравенство, в котором неизвестная содержится только в показателе степени при постоянном основании а, а > 0, a  1.

Типы неравенств и способы их решения

Всюду далее f(x), g(x), h(x) – некоторые выражения с переменной.

I тип: неравенство вида

(6.12)

где b  R.

Если то решением неравенства (6.12) является множество всех x из ОДЗ выражения f(x).

Если логарифмированием по основанию a неравенство (6.12) сводится к равносильному неравенству. При этом существенно учитывается величина основания a:

1) если то в результате логарифмирования получают неравенство

2) если то после логарифмирования приходят к неравенству

Далее решают в зависимости от вида выражения f(x).

Если исходное неравенство имело знак < или , или , то аналогично знак неравенства меняется на противоположный в случае и не изменяется в случае

II тип: неравенство вида

(6.13)

Для решения неравенства (6.13) (или аналогичных ему со знаками , <, ) используют монотонность логарифма:

1) если 0 < a < 1, то неравенство (6.13) равносильно неравенству

которое решают в зависимости от вида выражений f(x) и g(x);

2) если то неравенство (6.13) равносильно неравенству

III тип: неравенство вида

(6.14)

где F – некоторое выражение относительно

Вводят замену переменной и решают относительно переменнойy неравенство

Найденные в качестве решения промежутки (если такие существуют) записывают в виде неравенств относительно y и затем возвращаются к переменной x. Остается решить полученные показательные неравенства.

Если переменная содержится и в основании степени, и в показателе, то такое неравенство называется показательно-степен­ным. Поскольку изменение знака неравенства зависит от величины основания, то для показательно-степенных неравенств рассматривают два случая, т. е. решают совокупность систем неравенств.

Показательно-степенные неравенства решают при условии, что основание степени положительно.

В частности, аналогом показательного неравенства (6.13) является следующее показательно-степенное неравенство

(6.15)

Его решение сводится к решению совокупности:

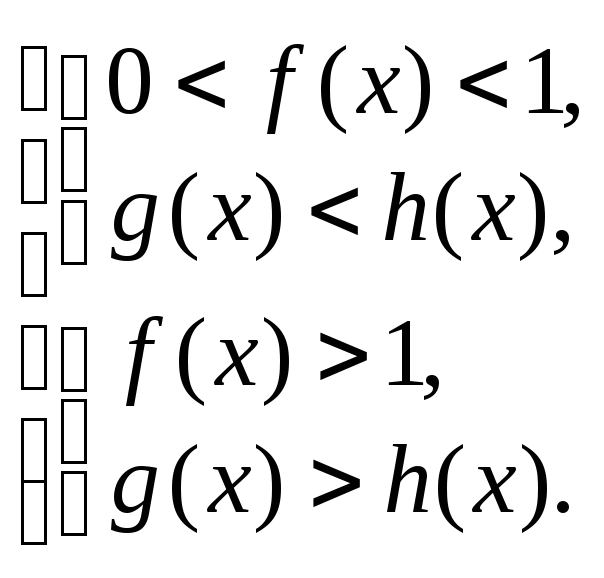
Пример 1. Решить неравенство и в ответе указать меньшее целое решение.

Решение. Преобразуем неравенство к виду

т. е.

Получили неравенство I типа. Решаем логарифмированием по основанию 2. Поскольку основание степени – число 2 и 2 > 1, то знак неравенства сохраняется:

Получили Определим, между какими последовательными целыми числами находится числоИспользуя монотонность логарифма, имеем:

т. е.

Тогда

Следовательно,

Число –5 – меньшее целое решение, которое принадлежит промежутку

Получаем ответ: х = –5.

Пример 2. Решить неравенство

Решение. Запишем неравенство в виде

Получили неравенство II типа. Поскольку основание степени число и то знак неравенства изменится на противоположный. Получаем неравенство:

т. е. и

Получили ответ:

Пример 3. Найти сумму целых решений неравенства

Решение. Преобразуем неравенство к виду

Разделив обе части неравенства на получим:

Получили квадратное неравенство относительно (неравенство III типа). Заменяем и решаем квадратное неравенство

Его решением является т. е.

Возвращаемся к исходной неизвестной величине:

Получаем множество решений: x  [–2; 0].

Целыми решениями являются числа: x = –2, x = –1 и x = 0.

Их сумма равна:

Получаем ответ: –3.

Задания