I уровень

1.1. Найдите область определения функции:

1) 2)3)4)

5) 6)7)

1.2. Вычислите значение функции в точке:

1) –2; 2) 3) 0; 4)5) 1; 6) 2.

1.3. Вычислите значение функции в точке:

1) –2; 2) 3) 0; 4)5) 1; 6) 2.

1.4. Вычислите если:

1) 2)3)4)

1.5. Постройте в одной системе координат графики функций Опишите их взаимное расположение.

1.6. Постройте график функции:

1) 2)3)

4) 5)6)

7) 8)9)

1.7. Исследуйте функцию на монотонность:

1) 2)3)

4) 5)6)

7) 8)

1.8. Сравните числа:

1) и2)и

3) и4)и

5) и6)и

7) и8)и

9) и10)и

11) и12)и

13) и14)и

15) и16)и

17) и 1; 18)и

II уровень

2.1. Найдите область определения функции:

1) 2)

2.2. Постройте график и найдите область значений функции:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

2.3. Решите уравнение графически:

1) 2)

III уровень

3.1. Постройте график функции:

1) 2)

3) 4)

3.2. Докажите тождество:

1) 2)

3) 4)

5) 6)

7)

8)

9)

10)

11)

12)

3.3. Решите уравнение графически:

1) 2)

6.2. Понятие логарифма и его свойства

Логарифмом числа b (b  0) по основанию а (а  0, а  1) называют показатель степени, в которую нужно возвести число а, чтобы получить число b:

(6.1)

Формулу (6.1) называют основным логарифмическим тождеством.

Логарифм числа b по основанию 10 называется десятичным логарифмом и обозначается

Логарифм по основанию e (e = 2,71828…) называется натуральным логарифмом и обозначается

Свойства логарифмов

Пусть Тогда:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11) тогда и только тогда, когда

12) тогда и только тогда, когда

13) тогда и только тогда, когда

Обобщенные свойства логарифмов

Пусть и– выражения с переменной. Тогда:

3^*) где

4^*) где

5^*) где

6^*) где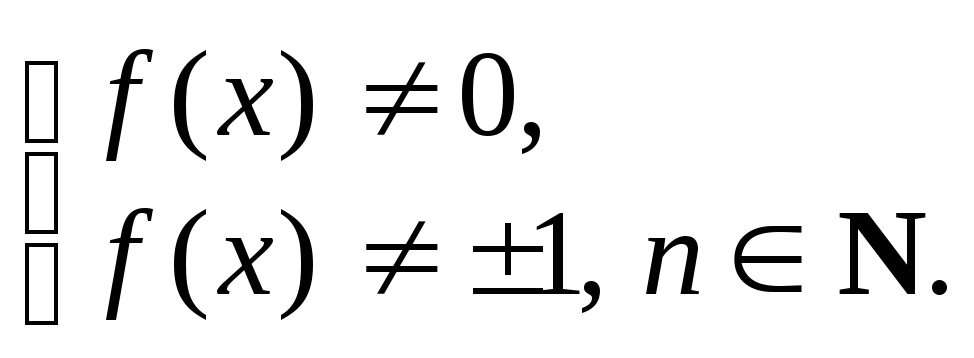

З а м е ч а н и е 1. Следует различать произведение логарифмов и повторный логарифм

З а м е ч а н и е 2. Степень логарифма может быть записана двумя способами:

или

Логарифмированием называется операция нахождения логарифма числа или выражения.

Потенцированием называют действие, обратное логарифмированию, т. е. потенцирование – это операция нахождения числа (выражения) по его логарифму. При выполнении этих операций пользуются свойствами логарифмов.

Пример 1. Упростить выражение

Решение. Преобразуем каждое слагаемое отдельно. При этом сделаем ссылку на конкретные свойства логарифмов, приведенные выше.

используем свойство 9 |по свойству 5|=по основному логарифмическому тождеству

по свойству 10

тогда

по свойству 5 =

= по свойству 2 =

по свойству 8

Таким образом:

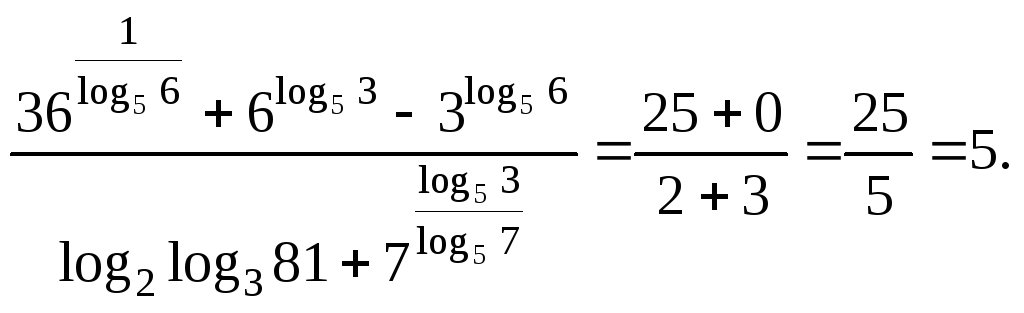
З а м е ч а н и е 3. Решение этого примера при одновременном преобразовании всех слагаемых (что и следует делать) выглядит так:

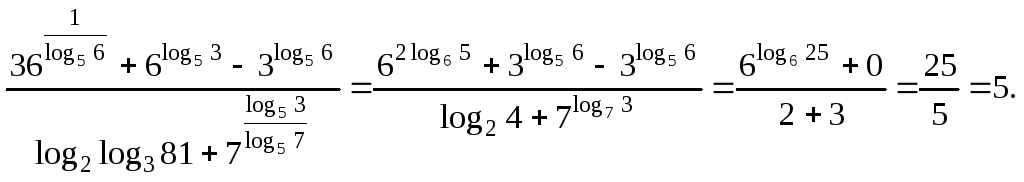
Пример 2. Вычислить

Решение. Для преобразования первого и второго слагаемых используем формулу изменения основания логарифма (свойство 9), а затем свойства 3 и 5.

= по свойствам 5 и 2 =

Для преобразования третьего слагаемого используем свойства 3–5:

Тогда получаем:

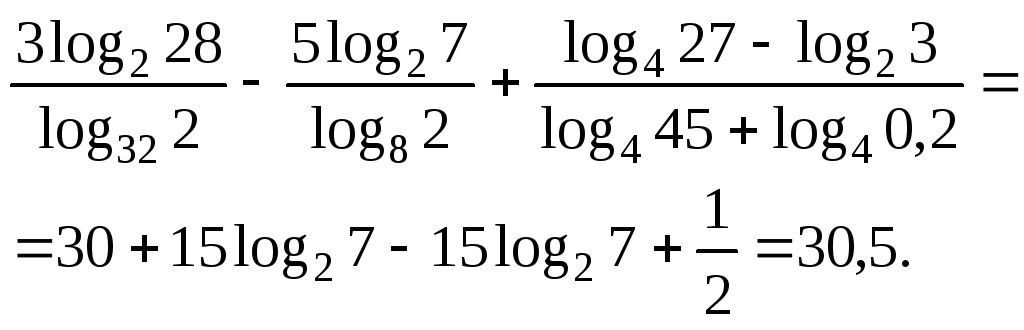
З а м е ч а н и е 4. Подробное описание решения и преобразование всех слагаемых отдельно приведено исходя из соображений доступности объяснений. Целесообразно делать преобразования всего выражения сразу, аналогично тому, как сделано в замечании 1.

Пример 3. Прологарифмировать по основанию 10 выражение

Решение. Замечаем, что сделать это можно, если Тогда

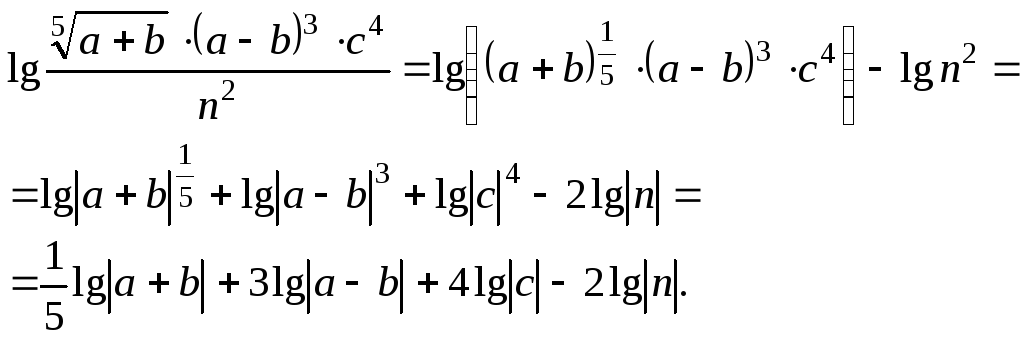
Пример 4. Выполнить потенцирование выражения

Решение. Используем свойства логарифмов 3–5 («справа–налево»):

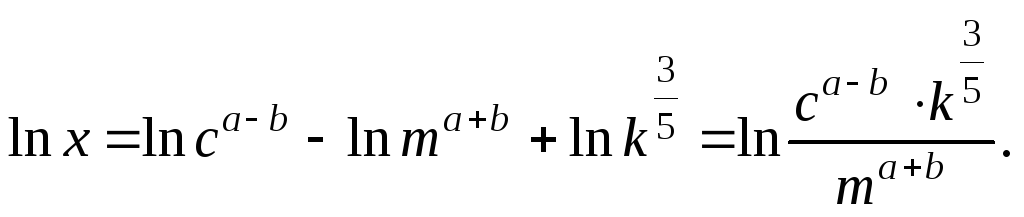
Получаем ответ:

Пример 5. Выразить черези

Решение.

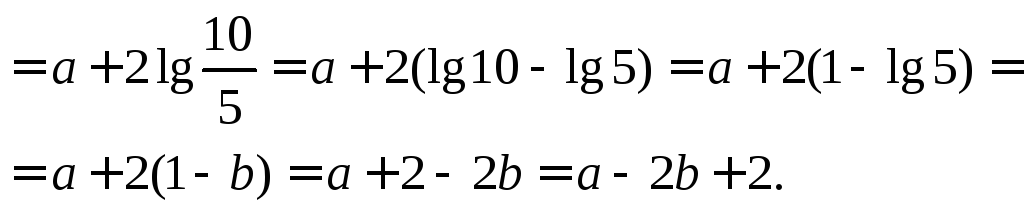
Задания