
- •7. Тригонометрия
- •7.1. Тригонометрические функции
- •I уровень
- •II уровень
- •III уровень
- •7.2. Основные тригонометрические формулы
- •I уровень
- •II уровень
- •III уровень
- •7.3. Графики тригонометрических функций
- •I уровень
- •II уровень
- •III уровень
- •7.4. Обратные тригонометрические функции
- •I уровень
- •2. Уравнения, решаемые разложением на множители
- •3. Уравнения, решаемые с помощью формул
- •4. Уравнения, решаемые с помощью замены переменной
- •5. Однородные уравнения
- •6. Неоднородные уравнения 2-й степени
- •7. Неоднородные уравнения 1-й степени
- •8. Уравнения, решаемые с применением формул
- •9. Уравнения, решаемые методом универсальной
- •10. Уравнения, решаемые применением ограниченности
- •I уровень
- •II уровень
- •III уровень
- •7.6. Тригонометрические неравенства
- •I уровень
- •II уровень
- •III уровень
- •7.7. Тригонометрическая и показательная формы
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1.Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
II уровень
2.1.Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
III уровень
3.1.Решите неравенство:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7.7. Тригонометрическая и показательная формы
комплексного числа
Комплексное число
![]() в прямоугольной декартовой системе
координатОхуизображается точкойМ(рис. 7.28).
в прямоугольной декартовой системе
координатОхуизображается точкойМ(рис. 7.28).

Рис. 7.28
Длина радиус-вектора точки Мназываетсямодулем комплексного числаzи обозначается |z| илиr:
![]() (7.31)
(7.31)
Угол , образованный этим вектором с положительным направлением действительной осиОх, называетсяаргументомчислаz. Связь между аргументомкомплексного числа и его действительной и мнимой частью выражается формулами:
![]() (7.32)
(7.32)
или
 (7.33)
(7.33)
Аргумент комплексного числа определен
неоднозначно: если – аргумент числаz,
то![]() – также аргумент этого числа при любом
целомk. Для однозначности
определения аргумента его выбирают в
пределах
– также аргумент этого числа при любом
целомk. Для однозначности
определения аргумента его выбирают в
пределах![]()
![]() такое значение аргумента называютглавными обозначают
такое значение аргумента называютглавными обозначают![]() Всюду далее будем рассматривать главное
значение аргумента:
Всюду далее будем рассматривать главное
значение аргумента:![]()
На практике находить аргумент комплексного числа zимеет смысл согласно формуле (7.32) с учетом координатной четверти, в которой лежит числоz, или формул (7.33).
Запись комплексного числа в виде
![]() (7.34)
(7.34)
называется тригонометрической формой комплексного числа.
Пусть
![]() и
и![]() комплексные числа, заданные в
тригонометрической форме. Тогда для
произведения
комплексные числа, заданные в
тригонометрической форме. Тогда для
произведения![]() и частного
и частного![]() справедливы формулы:
справедливы формулы:
![]() (7.35)
(7.35)
![]() (7.36)
(7.36)
Для комплексного числа
![]() справедливаформула Муавра:
справедливаформула Муавра:
![]() (7.37)
(7.37)
Корнем n-й
степенииз комплексного числаzназывается комплексное числоwтакое, что![]()
Корень n-й степени из комплексного числа
![]()
имеет nразличных значений, которые находят по формуле
![]() (7.38)
(7.38)
где
![]()
![]() – арифметическое значение корня.
– арифметическое значение корня.
Все значения корня
![]()
![]() расположены на окружности с центром в
начале системы координат и радиусом
расположены на окружности с центром в
начале системы координат и радиусом![]() в вершинах правильного вписанного в
окружностьn-угольника.
в вершинах правильного вписанного в
окружностьn-угольника.
Соотношение
![]() (7.39)
(7.39)
называется формулой Эйлера.
Пусть комплексное число zзаписано в тригонометрической форме. Используя формулу Эйлера (7.39), можно записать:
![]() (7.40)
(7.40)
Такая форма записи называется показательной формойкомплексного числа.
Правила действий над комплексными числами
в показательной форме
![]() (7.41)
(7.41)
![]() (7.42)
(7.42)
![]() (7.43)
(7.43)
![]() где
где![]() (7.44)
(7.44)
Пример 1. Представить в тригонометрической форме комплексное число:
1)
![]() 2)
2)![]() 3)
3)![]()
Решение. 1) Находим модуль данного числа по формуле (7.31):
![]()
Для нахождения аргумента используем формулу (7.32):
![]()
и число z
лежит в IV
четверти. Поэтому
![]() (рис. 7.29).
(рис. 7.29).

Рис. 7.29
Подставим полученные значения |z| и в формулу (7.34), получим:
![]()
2) В данном случае
![]()
![]() (точка, изображающая данное число,
принадлежит отрицательной части мнимой
оси (рис. 7.30)).
(точка, изображающая данное число,
принадлежит отрицательной части мнимой
оси (рис. 7.30)).

Рис. 7.30
Поэтому
![]()
3) Находим модуль комплексного числа
![]()
(так как
![]() ),
),![]() (заданное число является отрицательным
действительным числом (рис. 7.31)).
(заданное число является отрицательным
действительным числом (рис. 7.31)).

Рис. 7.31
Поэтому
![]()
Пример 2. Выполнить действия:
1)
![]()
2)
![]()
3)
![]()
Решение. 1) Используя формулу (7.35), находим:
![]()
2) Сначала представим
число
![]() в тригонометрической форме. Имеем
в тригонометрической форме. Имеем![]() Поскольку число лежит вIV
четверти и
Поскольку число лежит вIV
четверти и
![]() то
то![]() Следовательно,
Следовательно,![]()
Теперь воспользуемся формулой (7.35):
![]()
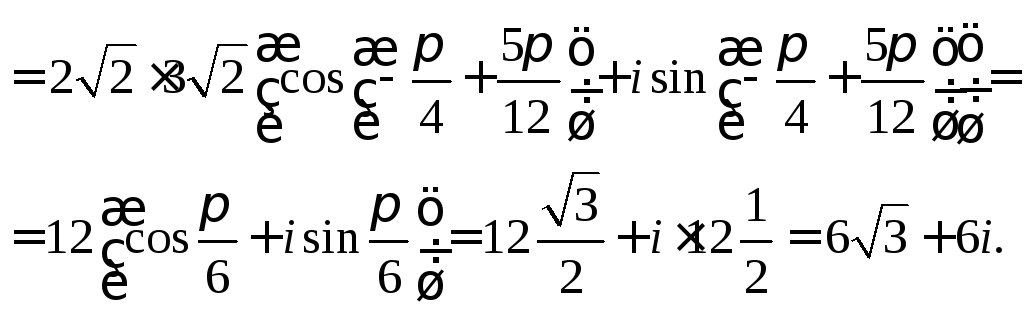
Получаем ответ:
![]()
3) Заметим, что делимое число не записано в тригонометрической форме. Запишем его в этой форме. Получим:
![]()
Используя формулу (7.36), находим:
![]()
![]()
![]()
Переходя к
алгебраической форме, получаем в ответе
![]()
Пример 3.
Возвести в степень выражение
![]()
Решение.
Представим число
![]() в тригонометрической форме. Здесь
в тригонометрической форме. Здесь![]()
![]() и соответствующая точка лежит воII
четверти, т. е.
и соответствующая точка лежит воII
четверти, т. е.
![]() Получили
Получили![]() По формуле (7.37) находим:
По формуле (7.37) находим:
![]()
Получаем ответ: 512.
Пример 4. Извлечь корень. Полученные значения корня изобразить на комплексной плоскости:
1)
![]() 2)
2)![]()
Решение.
1) Находим модуль и аргумент числа
![]()
Получаем
![]() Далее, используя формулу (7.38), вычисляем:
Далее, используя формулу (7.38), вычисляем:
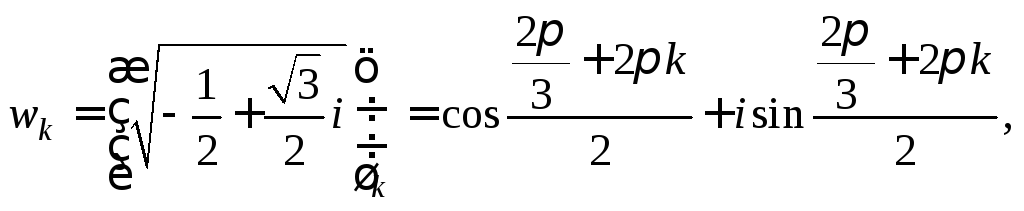
где
![]()
Если
![]() то
то![]()
если
![]() то
то![]() (рис. 7.32).
(рис. 7.32).

Рис. 7.32
2) Находим модуль
и аргумент числа
![]()
![]()
![]() Получили
Получили![]() Тогда, используя формулу (7.38), имеем:
Тогда, используя формулу (7.38), имеем:
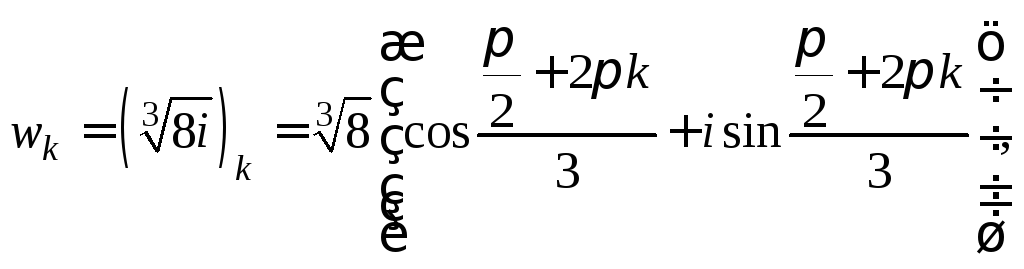
где
![]()
Если
![]() то
то![]()
если
![]() то
то
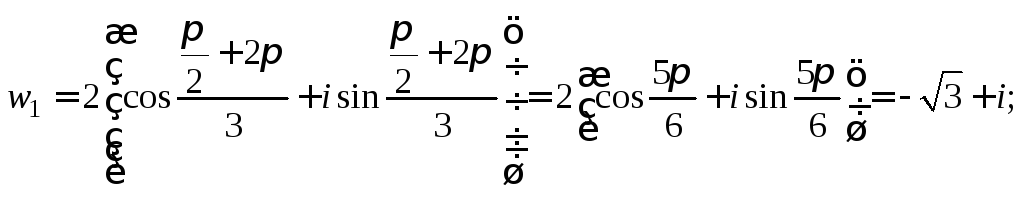
если
![]() то
то
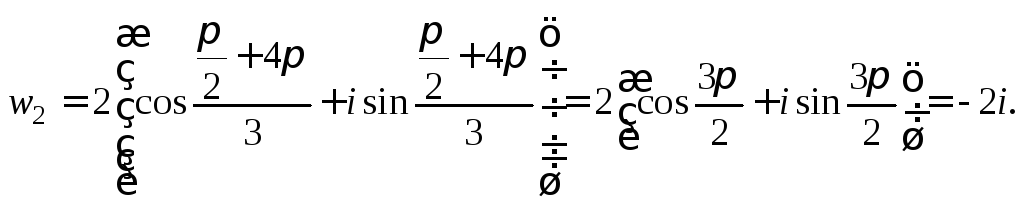
Изобразим комплексные
числа
![]() На комплексной плоскости точки,
соответствующие значениям корня,
являются вершинами правильного
треугольника, вписанного в окружность
радиусом
На комплексной плоскости точки,
соответствующие значениям корня,
являются вершинами правильного
треугольника, вписанного в окружность
радиусом![]() с центром в начале координат (рис. 7.33).
с центром в начале координат (рис. 7.33).

Рис. 7.33
Пример 5. Представить число в показательной форме:
1)
![]() 2)
2)![]()
Решение.
1) Находим модуль и аргумент комплексного
числа
![]()
![]()
![]() и число лежит воII
четверти, следовательно
и число лежит воII
четверти, следовательно
![]() Получили
Получили![]()
2) Находим модуль
и аргумент комплексного числа
![]()
![]()
![]() Тогда, по формуле (7.40) имеем:
Тогда, по формуле (7.40) имеем:
![]()
Пример 6.
Решить
уравнение
![]()
Решение.
![]() Искомыми корнями уравнения будут
значения
Искомыми корнями уравнения будут
значения![]()
Для
![]() имеем
имеем![]()
![]() Тогда
Тогда![]() По формуле (7.44) получаем:
По формуле (7.44) получаем:
![]()
где k = 0, 1, 2.
Если k
= 0, то
![]()
если k
= 1, то
![]()
если k
= 2, то
![]()
Таким образом, корнями заданного уравнения являются числа:
![]()
![]()
![]()
Пример 7. Изобразить на комплексной плоскости множество точек, для которых:
1)
![]() 2)
2)![]() 3)
3)
Решение.
1) Пусть
![]() тогда
тогда
![]()
Найдем модуль полученного комплексного числа
![]()
Тогда заданное равенство будет иметь вид:
![]() или
или
![]()
Э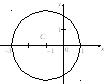 то
уравнение окружности радиуса 2 с центром
в точке
то
уравнение окружности радиуса 2 с центром
в точке![]() (рис. 7.34).
(рис. 7.34).
Рис. 7.34
2) Пусть
![]() Из условия имеем
Из условия имеем![]() Геометрически это неравенство задает
на плоскости множество точек, лежащих
внутри угла с вершиной в точке (0; 0),
стороны которого составляют с положительным
направлением осиОх
углы
Геометрически это неравенство задает
на плоскости множество точек, лежащих
внутри угла с вершиной в точке (0; 0),
стороны которого составляют с положительным
направлением осиОх
углы
![]() и
и![]() а также множество точек, лежащих на луче
а также множество точек, лежащих на луче![]() (рис. 7.35).
(рис. 7.35).
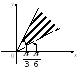
Рис. 7.35
3) Заданная система равносильна следующей:

Решением системы
будет пересечение множества точек,
лежащих вне окружности
![]() и множества точек, лежащих внутри угла
величины
и множества точек, лежащих внутри угла
величины![]() и на его сторонах (рис. 7.36).
и на его сторонах (рис. 7.36).

Рис. 7.36
Задания
