4. Уравнения, решаемые с помощью замены переменной

Пример 8. Решить уравнение

Решение. Данное уравнение является квадратным относительно Заменяемполучим уравнениеЕго корнииТаким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:

Уравнение корней не имеет, т. е.

Решением второго является:

Получаем ответ:

Пример 9. Решить уравнение

Решение. Используем тождество и формулуУравнение сводится к виду

Мы получили квадратное уравнение относительно Заменяемполучим уравнениеоткуда

Приходим к совокупности простейших уравнений:

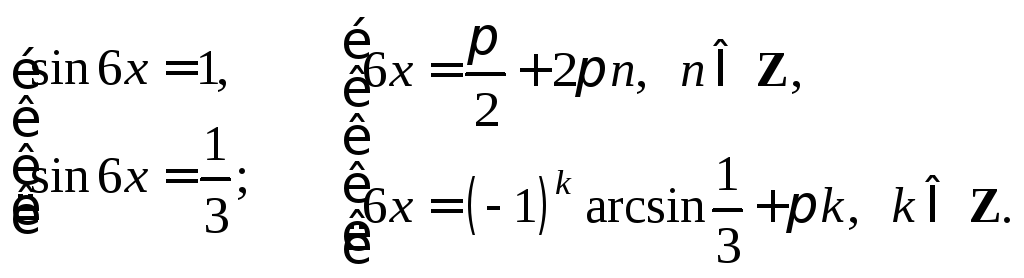
Получаем ответ:

Пример 10. Найти сумму корней уравнения

если

Решение. поскольку

Упростим исходное уравнение:

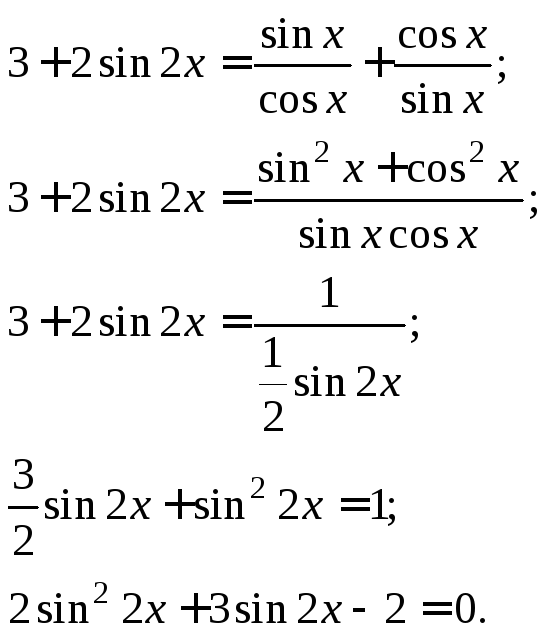
Получили квадратное уравнение относительно Сделав заменугдеимеем уравнениеоткудаили

Вернувшись к прежней неизвестной, получим совокупность уравнений:

Первое уравнение не имеет решения. Решаем второе:

Придаем n значение n = 0, получаем:

при n = 1 имеем

Нетрудно убедиться, что при всех других значениях n корни не попадут на отрезок Значит сумма корней, принадлежащих отрезкуравна

Получаем ответ:

5. Однородные уравнения

Однородным тригонометрическим уравнением n-й степени относительноиназывается уравнение вида

(7.27)

где – действительные числа,

В уравнении (7.27) так как приисходное уравнение примет вид:откудачто невозможно, посколькуине могут одновременно равняться нулю.

Разделив исходное уравнение на получим:

С помощью замены имеем алгебраическое уравнение

которое решаем и возвращаемся к старой переменной.

Пример 11. Решить уравнение

Решение. Разделив уравнение на получимоткудаи

Получаем ответ:

Пример 12. Решить уравнение

Решение. Используя формулу приведем данное уравнение к однородному:

Разделим почленно на

откуда

Введем замену и получим уравнениекорнями которого будут

После чего перейдем к решению совокупности простейших уравнений:

Получаем ответ:

6. Неоднородные уравнения 2-й степени

Неоднородным тригонометрическим уравнением 2-й степени называется уравнение вида

(7.28)

Используя основное тригонометрическое тождество, приводим уравнение к однородному

которое решаем далее как уравнение (7.27).

Пример 13. Решить уравнение

Решение. Используя формулы:

и

преобразуем данное уравнение к однородному:

Разделим на

Введем замену

откуда

Решим совокупность уравнений:

Получаем ответ:

7. Неоднородные уравнения 1-й степени

Неоднородным уравнением 1-й степениназывается уравнение вида

(7.29)

1-й способ решения. Используем формулы двойного аргумента:

Тогда уравнение (7.29) сводится к однородному уравнению 2-й степени, которое решаем как уравнение (7.28).

2-й способ решения.Используем метод введения вспомогательного аргумента.

Разделив обе части уравнения (7.29) на получим:

Так как то существует угол, такой, что

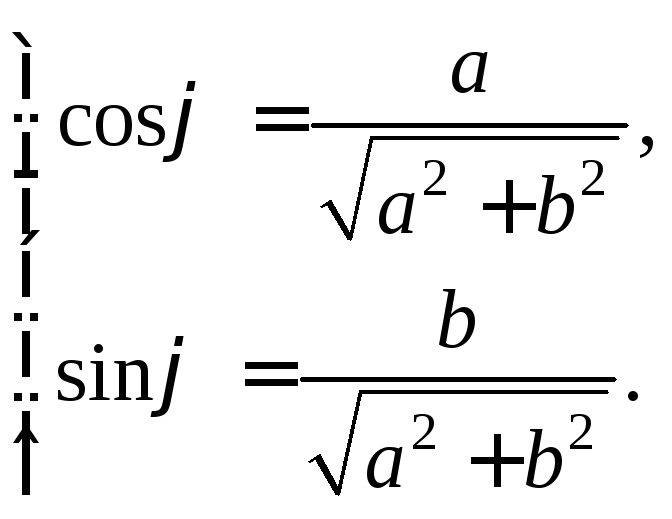(7.30)

Тогда исходное уравнение (7.29) примет вид:

или, используя формулу (7.8) для синуса суммы, получим:

Если то последнее уравнение имеет решение:

Угол находят из формулы (7.30), например,

Приходим к ответу:

Пример 14. Решить уравнение

Решение. Разделив левую и правую часть уравнения на (так как), получим:

Тогда

и

откуда

Таким образом, получаем уравнение:

откуда приходим к ответу: