I уровень
1.1.Найдите область определения функции:
1)
2)
3)
4)
1.2.Найдите множество значений функции:
1)
2)
3)
4)
5)
1.3.Выясните, является ли данная функция четной или нечетной:
1)
2)
3)
4)
5)
1.4.Найдите наименьший положительный период функции:
1)
2)
3)
4)
5)
6)
7)
8)
1.5.Используя свойства возрастания
и убывания функций
сравните числа:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
1.6. Постройте график функции, используя правила преобразования графиков:
1)
2)
3)
4)
5)
6)
7)
8)
II уровень
2.1.Найдите область определения функции:
1)
2)
3)
4)
2.2.Найдите множество значений функции:
1)
2)
3)
4)
5)
2.3. Выясните, является ли данная функция четной или нечетной:
1)
2)
3)
4)
5)
6)
7)
2.4.Найдите наименьший положительный период функции:
1)
2)
3)
4)
2.5.Постройте график функции, используя правила преобразования:
1)
2)
3)
4)
5)
6)
III уровень
3.1.Найдите область определения функции:
1)
2)
3)
4)
5)
3.2.Найдите множество значений функции:
1)
2)
3)
4)
5)
6)
3.3.Выясните, является ли данная функция четной или нечетной:
1)
2)
3)
4)
3.4.Найдите наименьший положительный период функции:
1)
2)
3)
4)
3.5. Найдите наибольшее и наименьшее значения функции:
1)
2)
3.6.Постройте график функции, используя правила преобразования графиков функции:
1)
2)
3)
4)
3.7.Определите вид графика функции
и постройте его, используя правила
преобразования:
1)
2)
3)
4)
5)
6)
7)
3.8.Найдите абсциссы общих точек графиков функций
и
7.4. Обратные тригонометрические функции
Функция
на отрезке
имеет обратную функцию, которая называетсяарксинусом.
Арксинусом числа х, где
называется такое числоу,
синус которого равен числух.
Обозначают:
Таким образом,
– это уголу, измеренный в радианах,
такой, что
Свойства арксинуса
где
где
График функции
приведен на рис. 7.15.
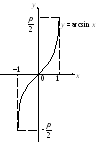
Рис. 7.15
Функция
на отрезке
имеет обратную функцию, которая называетсяарккосинусом.
Арккосинусом числа х,
где
называется такое числоу,
косинус которого равен числух.
Обозначают:
Таким образом,
– это уголу, измеренный в радианах,
такой, что
Свойства аркксосинуса
где
где
График функции
приведен на рис. 7.16.
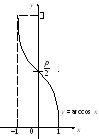
Рис. 7.16
Функция
на промежутке
имеет обратную функцию, которая называетсяарктангенсом.
Арктангенсом числа х,
называется такое числоу,
тангенс которого равен числух.
Обозначают:
Таким образом,
– это уголу, измеренный в радианах,
такой, что
Свойства арктангенса
где
где
График функции
приведен на рис. 7.17.
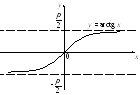
Рис. 7.17
Функция
на промежутке
имеет обратную функцию, которая называетсяарккотангенсом.
Арккотангенсом числа х,
называется числоу, 
котангенс которого равен числух.
Обозначается:
Таким образом,
– это угол у, измеренный в радианах,
такой, что
Свойства арккотангенса
где
где
График функции
приведен на рис. 7.18.
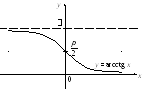
Рис. 7.18
Для обратных тригонометрических функций выполняются следующие равенства:
(7.16)
(7.17)
Пример 1. Проверить, справедливы ли равенства:
1)
2)
3)
4)
Решение.
1)
так как
и
Равенство верно.
2)
так как
и
Равенство верно.
3)
так как
и
Равенство верно.
4)
так как
и
Равенство верно.
Пример 2. Вычислить
Решение. Вычислим слагаемые отдельно, чтобы прокомментировать действия.
функция нечетная и
так как
и
Поэтому
(по свойству) и
так
как
и
Поэтому
так как
и
(по свойству) и
так
как
и
Поэтому
Таким образом,
Получаем ответ:
Пример 3.
Решить
уравнение
Решение.
Поскольку
то
т. е.
Находим:
откуда
приходим к ответу
Пример 4.
Найти
область значений функции
Решение.
Поскольку
то
и
Получаем ответ:
Пример 5.
Вычислить
Решение.
Используя
свойство функции
для отрицательного аргумента и формулу
приведения для
получаем:
Для дальнейших
вычислений необходимо выразить функцию
через
чтобы воспользоваться затем формулой
Из формулы
выражаем
если
Для нашего случая имеем:
Получаем ответ:
Пример 6.
Построить
график функции
Решение.
Для построения будем использовать
правила преобразования графика функции
(рис. 7.15).
Рассмотрим
последовательность преобразований,
позволяющих из графика функции
получить график заданной функции.
Преобразуем данную функцию следующим
образом:
Выполним построение поэтапно.
1
.
График функции
может быть получен из графика
(рис. 7.15) путем растяжения вдоль осиОу
в 2 раза (рис. 7.19).
Рис. 7.19
2. График функции
может быть получен из графика функции
путем растяжения вдоль осиОх
в 2 раза (рис. 7.20).
Рис. 7.20
3. График функции
может быть получен из графика функции
путем параллельного переноса вдоль осиОх
на 2 единицы влево (рис. 7.21).
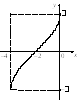
Рис. 7.21
4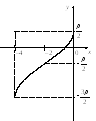
.
График функции
получаем из графика
путем параллельного переноса вдоль осиОу
на
единиц вниз (рис. 7.22).
Рис. 7.22
Пример 7. Построить на единичной окружности угол , такой, что
1)
2)
Решение.
1) Воспользуемся определением синуса.
Равенству
соответствуют два угла
и
(рис. 7.23).
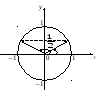
Рис. 7.23
2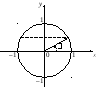
)
По определению арксинуса
На данном промежутке существует только
один угол, синус которого равен
т. е.
(рис. 7.24).
Рис. 7.24
Пример 8.
Решить
уравнение
Решение. Формула (7.16) позволяет перейти к системе
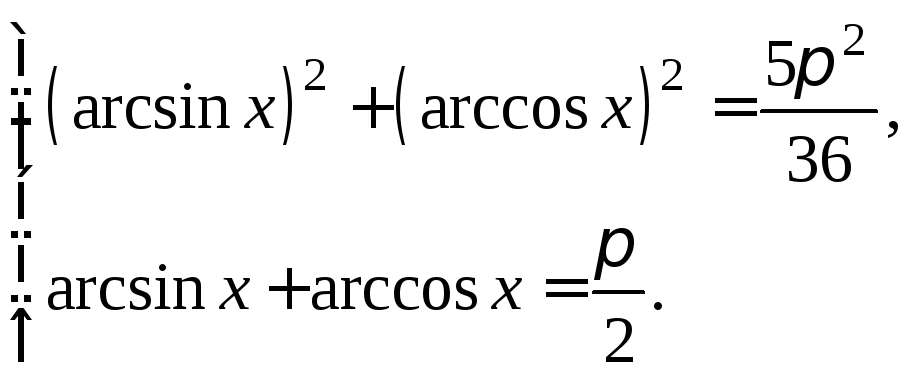(7.18)
Пусть
где
Тогда система (7.18)
приобретает вид:
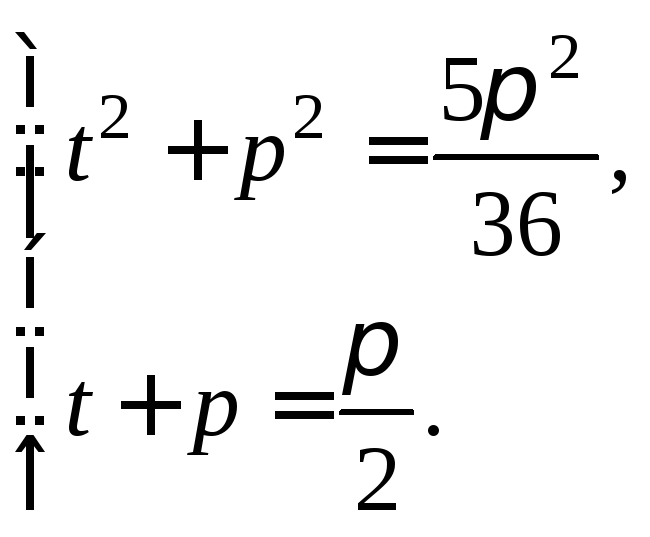
Решим последнюю
систему и получим:
или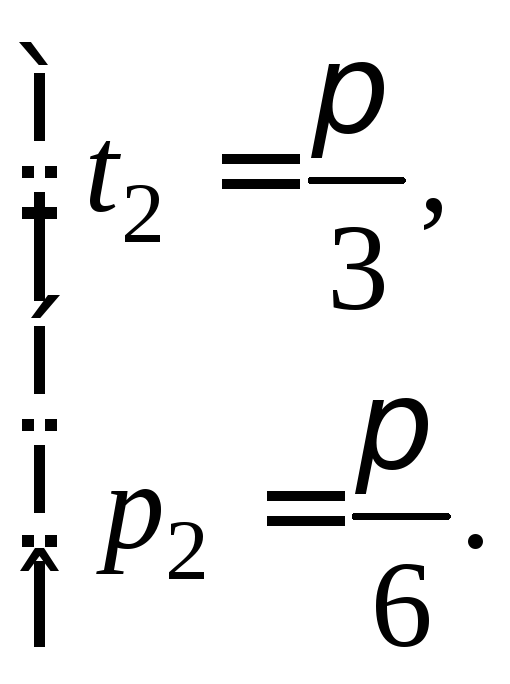
Отсюда
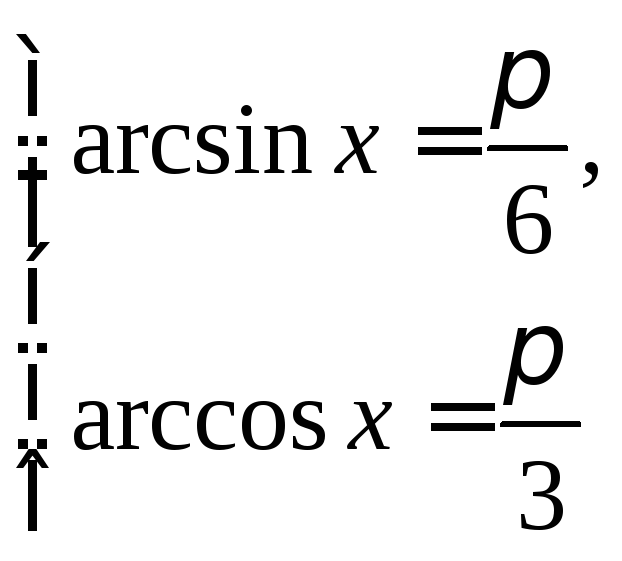или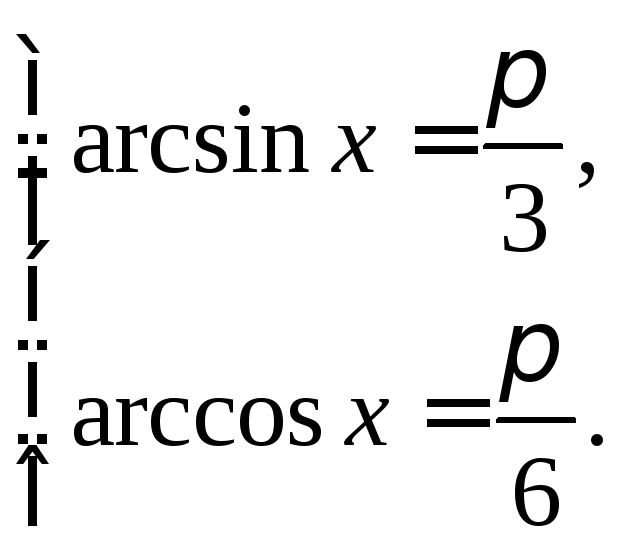
Обе эти системы
имеют решение. Из первой системы получаем
а вторая дает
Получаем ответ:
Задания