8. Уравнения, решаемые с применением формул

понижения степени

При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени (7.12).

Пример 15. Решить уравнение

Решение. Используем формулу Заданное уравнение примет вид:

Преобразуя, перейдем к решению уравнения

откуда

Применив формулы (7.13) преобразования суммы и разности косинусов в произведение, получим:

или

откуда

Получаем совокупность уравнений:

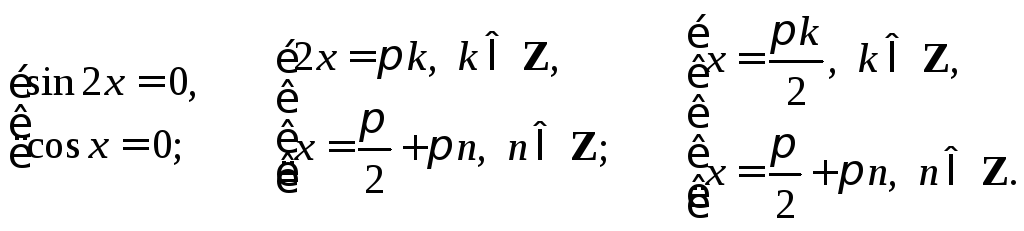
Множество решений содержится во множестве решений

Поэтому приходим к ответу:

9. Уравнения, решаемые методом универсальной

подстановки

Тригонометрическое уравнение, рациональное относительно может быть сведено к рациональному уравнению относительнос помощью формул универсальной подстановки (7.15).

Следует отметить, что применение формул (7.15) может привести к сужению ОДЗ исходного уравнения, поскольку не определен в точкахПоэтому в таком случае нужно проверять, являются ли значениякорнями исходного уравнения.

Пример 16. Решить уравнение

Решение. По условию задачи Применим формулу (7.15) и преобразуем уравнение к виду

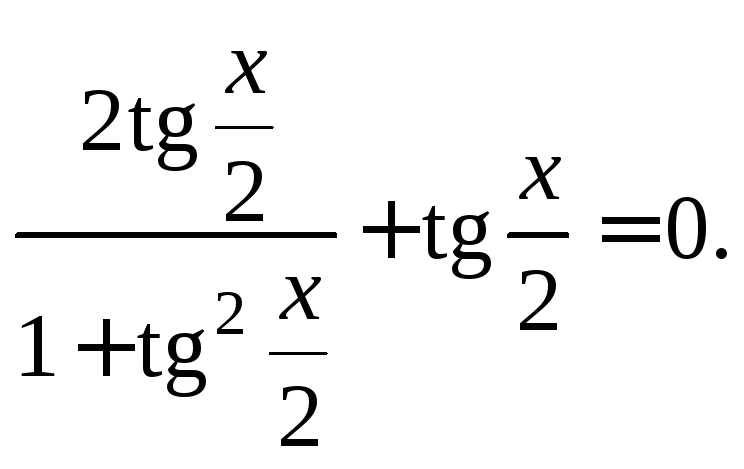
Сделав замену получим:

откуда и, следовательно,Решая последнее уравнение, получаем ответ:

10. Уравнения, решаемые применением ограниченности

тригонометрических функций

Рассмотрим уравнения, решение которых основано на следующем утверждении: если при решении уравнения удалось установить, что для всех допустимых значений переменнойхвыполняетсяи(а– константа), то данное уравнение равносильно системе

При решении уравнений, содержащих тригонометрические функции надо помнить, что

и

Пример 17. Решить уравнение

Решение. Так как ато данное уравнение равносильно системе

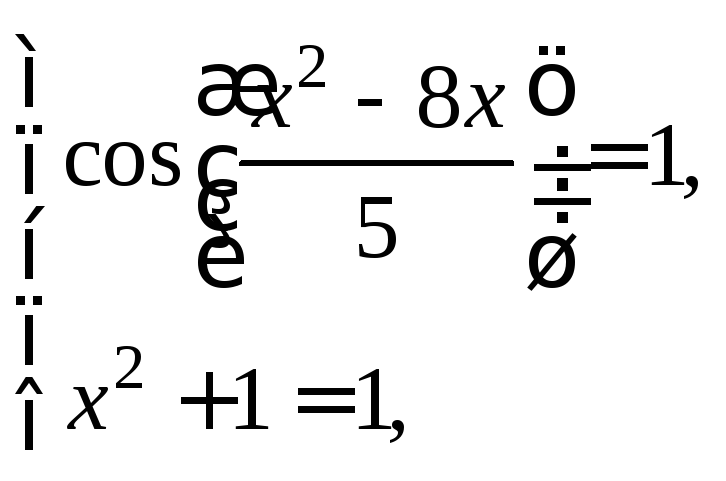
имеющей единственное решение

Получаем ответ:

Задания

I уровень

1.1.Решите тригонометрическое уравнение:

1) 2)

3) 4)

5) 6)

7) 8)

1.2.Решите уравнение:

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

25) 26)

27)

28)

II уровень

2.1. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)

28)

29)

30) Найдите сумму корней уравнения на отрезке

III уровень

3.1. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12) Найдите наименьшее целое решение уравнения, удовлетворяющее условию

13) Найдите все решения уравнения удовлетворяющие условию

14)

15)

16)

17)

18)

19) Найдите сумму корней уравнения, принадлежащих отрезку

20) Найдите количество корней, принадлежащих промежутку

3.2.Решите уравнение:

1) 2)

3) 4)

3.3.Найдите все значения параметраа, при которых уравнение имеет хотя бы одно решение:

1) 2)

3)

7.6. Тригонометрические неравенства

Для решения тригонометрических неравенств используют единичную окружность и определение тригонометрических функцийили графический метод, а также метод замены переменной.

Простейшие тригонометрические неравенства

и неравенства, сводящиеся к ним

Пример 1. Решить неравенство

Решение. Воспользуемся определением синуса. С помощью единичной окружности находим вначале углы х, которые соответствуют равенству Их два:и(рис. 7.25). Строим их, причем соответствующие радиус-векторы пунктиром, так как заданное неравенство строгое.

Выделим на единичной окружности множество точек, ординаты которых больше этоИспользуя периодичность функцииприходим к ответу:

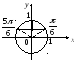
Рис. 7.25

Ответ неравенства следует понимать как объединение всех промежутков, которые получаем при всех

Пример 2. Решить неравенство

Решение. Заменив 3x + 1 на t, получим: Выделим на единичной окружности множество точек, абсциссы которых меньше или равны(рис. 7.26). Получим:

Учитывая период, имеем:

Возвращаемся к заданной неизвестной:

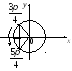
Рис. 7.26

Приходим к ответу:

Пример 3. Решить неравенство

Решение. Используем графический метод. Построим график функции для промежуткаПроведем прямую(рис. 7.27). Находим промежуток оси абсцисс, для точек которого графикпроходит не ниже построенной прямой. Этот промежуток и будет решением неравенства на рассматриваемом интервале.

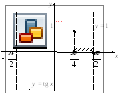
Рис. 7.27

С учетом периодичности функции приходим к ответу:

Пример 4. Решить неравенство

Решение.

Заменим Имеем:

т. е. получаем:

Возвращаемся к старой переменной:

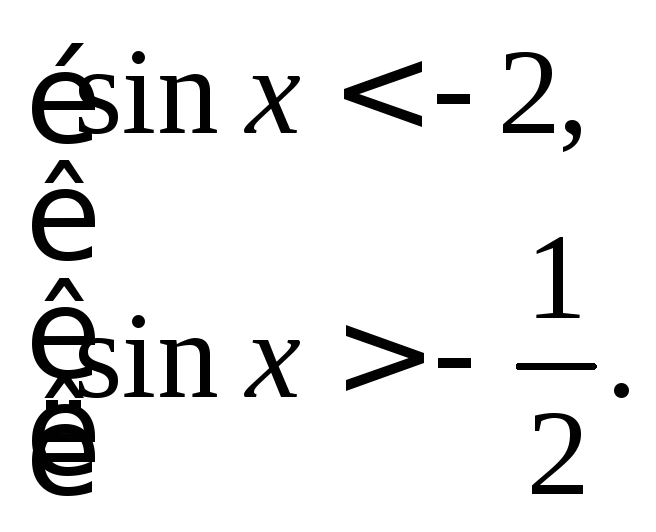
Первое неравенство совокупности решения не имеет. Решаем второе. С помощью единичной окружности получаем:

Учитываем период и приходим к ответу:

Задания