II уровень
2.1.Вычислите:
1)
если
2)
если
3)
если
4)
если
5)
если
2.2.Упростите выражение:
1)
2)
3)
4)
5)
6)
7)
8)
2.3.Докажите тождество:
1)
2)
3)
4)
5)
2.4.Вычислите:
1)
2)
3)
4)
5)
2.5.Найдите наибольшее и наименьшее значения выражения:
1)
2)
3)
4)
2.6.Докажите, что
если
2.7.Преобразуйте в произведение выражение:
1)
2)
3)
2.8.Вычислите:
1)
2)
2.9.Докажите тождество:
1)
2)
3)
4)
5)
2.10.Упростите выражение:
1)
2)
3)
4)
5)
III уровень
3.1.Вычислите:
1)
если
2)
если
3)
4)
5)
3.2. Упростите выражение:
1)
где
2)
3)
4)
5)
3.3. Докажите тождество:
1)
2)
3)
3.4. Вычислите:
1)
если
2)
3)
если
3.5.Докажите тождество:
1)
2)
3.6.Найдите наибольшее и наименьшее значения выражения:
1)
2)
3)
3.7.Определите, рациональным или
иррациональным числом является
если известно, что
3.8.Преобразуйте в произведение выражение
3.9.Вычислите:
1)
2)
3.10.Докажите тождество
3.11.Упростите выражение:
1)
2)
3)
4)
5)
6)
7.3. Графики тригонометрических функций
При рассмотрении графиков тригонометрических функций предполагается, что числовой аргумент представляет угол, измеренный в радианах.
Соответствие, при котором каждому
действительному числу хсопоставляется
синус этого числа, называютфункцией
синуси обозначают
Свойства функции
приведены в табл. 7.3.
Графиком функции
является кривая, называемаясинусоидой(рис. 7.7).
Рис. 7.7
Соответствие, при котором каждому
действительному числу хсопоставляется
косинус этого числа, называютфункцией
косинуси обозначают
Свойства функции
приведены в табл. 7.3.
Графиком функции
является кривая, называемаякосинусоидой
(рис. 7.8).
Рис. 7.8
Соответствие, при котором каждому
действительному числу
сопоставляется тангенс этого числа,
называютфункцией тангенси
обозначают
Свойства функции
приведены в табл. 7.3.
Графиком функции
является кривая, называемаятангенсоидой(рис. 7.9).
Рис. 7.9
Соответствие, при котором каждому
действительному числу
сопоставляется котангенс этого числа,
называютфункцией котангенси
обозначают
Свойства функции
приведены в табл. 7.3.
График функции приведен на рис. 7.10.
Рис. 7.10
Пример 1.
Найти область
определения функции
Решение. Должно выполняться неравенство
т. е.
Таким образом,
D(у):
Пример 2.
Найти область
значений функции
Решение. Используя формулу двойного угла для синуса, получим:
Так как функция
ограничена, то
тогда
и
Таким образом,
Пример 3. Выяснить, является ли функция у(х) четной или нечетной.
Решение.
Функцию
можно исследовать на четность или
нечетность, если область определения
функции является симметричным относительно
нуля множеством и выполняется одно из
равенств. В данном случае
симметричное относительно нуля множество.
Рассмотрим
В силу четности косинуса и нечетности синуса, получим:
Таким образом,
выполняется
Следовательно, данная функция является
нечетной.
Пример 4.
Сравнить
числа
и
Решение.
Используем
свойство монотонности функции y = cos x
на определенных промежутках. Углы
и
принадлежат отрезку
на котором функцияy = cos x
убывает, и
при этом
Используя свойство убывающей функции,
по которому большему значению аргумента
соответствует меньшее значение функции,
приходим к ответу:
Пример 5.
Найти
наименьший положительный период функции
Решение. Преобразуем
Используя формулы
двойного аргумента и основное
тригонометрическое тождество, получим
функцию
график которой получается из графика
функцииy = cos x
с периодом
Воспользуемся правилом нахождения
периодаТ'
функции, полученной путем некоторых
преобразований периодической функции
y = cos x
с периодом
Таким образом,
наименьший положительный период функции
а значит и функции
равен .
Пример 6.
Найти
наибольшее и наименьшее значения функции
Решение. Используем формулу приведения и формулу преобразования суммы функций в произведение:
Так как
то
Таким образом,
а
Пример 7.
Построить
график функции
Решение.
Для построения
будем использовать правила преобразования
графика элементарной функции
параллельный перенос вдоль осейОх
и Оу,
сжатие и растяжение графика функции.
Рассмотрим
последовательность преобразований,
позволяющих из графика функции
получить график функции
Для начала преобразуем данную функцию следующим образом:
Выполним построение поэтапно.
1. График функции
может быть получен из графика
путем растяжения вдоль осиОу
в 2 раза (рис. 7.11).
Рис. 7.11
2. График функции
может быть получен из графика функции
путем сжатия вдоль осиОх
в 2 раза (рис. 7.12).
Рис. 7.12
3. График функции
может быть получен из графика
путем параллельного переноса вдоль осиОх
на
единиц
вправо (рис. 7.13).
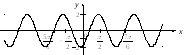
Рис. 7.13
4. График
получаем из графика
путем параллельного переноса вдоль осиОу
на 3 единицы
вверх (рис. 7.14).
Рис. 7.14
Задания