Задачи для самостоятельного решения

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10. BCBAC

2.11.

2.12.

2.13.

2.14.

2.15.

2.16.

2.17.

2.18.

2.19.

2.20.

2.21.

2.22.

2.23.

2.24. ABAC

2.25. ABCC

Контрольное задание №3. Упростить схему (рис. 2)

Рис. 2. Релейно-контактная схема

Методические указания

Релейно-контактная схема представляет собой устрой­ство из проводников и контактов, связывающих полюса ис­точников тока. Контакты могут быть размыкающими и за­мыкающими. Каждый контакт подключен к некоторому реле. Когда реле находиться под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - ра­зомкнуты.

Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замы­кающие контакты, подключенные к реле X, будем обозначать X₁,..., X_i, а размыкающие - ,..., .

Всей схеме также можно поставить одно из двух значе­ний: 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных X_i, (i,j = ), т.е. логи­ческая функция. Эту функцию называют функцией проводи­мости электрической цепи.

Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И, на­оборот, для некоторой схемы можно указать функцию прово­димости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основ­ные логические связки моделируются следующими элемен­тарными схемами:

1. X

2.

3. ХY

4. XY

т.е. дизъюнкция моделируется параллельными соединениями проводников, конъюнкция - последовательным.

Решение.

Построим функцию проводимости данной схемы, которая будет задаваться таблицей (табл. 4)

Таблица 4

Таблица истинности для релейно-контактной схемы

x	y	z	f
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

По данной логической функции построим СКНФ

СКНФ =

Упростим это выражение

=

Построим более простую схему, имеющую ту же функцию проводимости, что и исходная.

Рис. 3. Упрощенная релейно-контактная схема

Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить.

Построим схему электрической цепи, приведенной в примере, и упростим ее

Задачи для самостоятельного решения

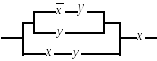
3.1.

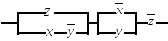
3.2.

3.3.

3

.4.

3.5.

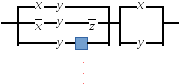
3.6.

3.7.

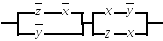
3.8.

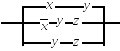
3.9.

3.10.

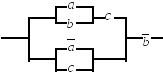
3.11.

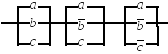
3.12.

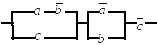
3.13.

3.14.

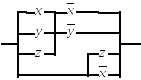
3.15.

3.16.

3.17.

3.18.

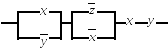
3.19.

3.20.

3.21.

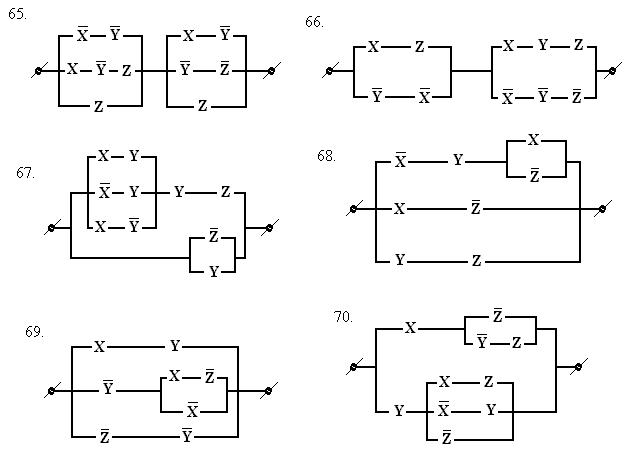
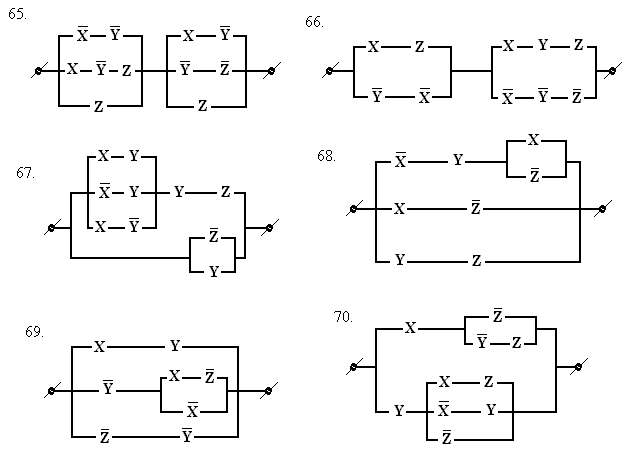
3.22.

3.23.

3.24.

3.25.

Контрольное задание № 4. Выяснить, каким из пяти замкнутых классов принадлежит функция, заданная своим характеристическим множеством(или представленная в табличной форме). Построить полином Жегалкина.

Методические указания

Алгебра над множеством логических функций с двумя бинарными операциями и, двумя константами 1,0 называется алгеброй Жегалкина, если в ней выполняются следующие законы:

; ;;;

xy = yx; x(yz) = (xy)z; xx = x

В алгебре Жегалкина дизъюнкция выражается формулой, из которой видно, чтотогда, когда xy = 0 (когда x и y ортогональны).

Всякую формулу алгебры Жегалкина можно представить в виде полинома Жегалкина.

Для всякой логической функции существует единственный полином Жегалкина.

Алгоритм построения полинома Жегалкина логической функции состоит из следующих шагов:

1) построить формулу с использованием связок или построить СДНФ функции;

2) заменить всюду на . Если построена СДНФ, заменить в ней все операциина операции, т.к. для ортогональных элементарных конъюнкций имеет место соотношение , если

3) раскрыть скобки, пользуясь дистрибутивным законом и привести подобные члены, используя правило алгебры Жегалкина

Рассмотрим логические функции ,. Будем считать, что функциизависят от одних и тех же аргументов. Это можно достигнуть, добавив при необходимости к аргументам некоторых функций фиктивные переменные (аргументы).

Некоторый класс А логических функций назовём замкнутым, если для всяких функций ,изА их суперпозиция

содержится в А.

Перечислим пять замкнутых классов логических функций:

1. Класс функций , сохраняющих константу 0, содержит функции, обладающие свойством f(0,0,...,0) = 0

2. Класс функций , сохраняющие константу 1, содержит функции, обладающие свойством f(1,1,...,1) = 1

3. Класс линейных функций L, для которых полином Жегалкина линеен

, .

4. Класс самодвойственных функций S, для которых выполняется условие , т.е. на всех инверсных наборов значения функции различны.

5. Класс монотонных функций M, для которых выполняется условие монотонности f(A)≥f(A`) при А>А`. Здесь и- двоичные наборы. Набор А больше набора А`, если каждый элементнабора А больше или равен соответствующему элементунабора А`.

Рассмотрим совокупность R всех логических функций от n переменных. Система функций называетсяполной в классе R (базисом), если любую функцию из этого класса можно представить суперпозицией функций . Базис, для которого удаление любой из функций превращает полную систему в неполную, называетсяминимальным.

Теорема о функциональной полноте (критерий полноты системы логических функций). Система функций является полной тогда и только тогда, когда она целиком не содержится ни в одном из пяти замкнутых классов .

Решение

Строим таблицу истинности для функции.

Таблица 5

x1 x2 x3	f
0 0 0	0
0 0 1	1
0 1 0	0
0 1 1	1
1 0 0	0
1 0 1	1
1 1 0	0
1 1 1	1

Исходя из определения функций, сохраняющих константу 0 (ноль), сохраняющих константу 1 (единица), самодвойственных выясняем, что

Исходя из определения монотонности функций, следует, что функция , где_М - класс монотонных функций.

Построив для функции полином Жегалкина

==

убеждаемся в том, что он имеет линейный вид. Следовательно, , гдеL - класс линейных функций.