
Тест 15
Определитель матрицы
 равен
равен
1) 2 2) -3 3) -2 4) 1 5) 0
Пусть А=
 ,В=
,В= ,С=
,С= .
МатрицаД=2(А+В-С)
имеет вид
.
МатрицаД=2(А+В-С)
имеет вид
1) 2)
2)![]()
![]() 3)
3)![]() 4)(0 -3)
5)
4)(0 -3)
5)![]()
![]()
Матрица А-1=
 является обратной для матрицы
является обратной для матрицы
1)
![]() 2)(5)
3)
2)(5)
3)![]() 4)(0 5)
5)
4)(0 5)
5)![]()
![]()
Если (
 )
- решение системы линейных уравнений
)
- решение системы линейных уравнений ,то
,то равно 1)-1
2) 1
3) 5
4) -5
5) -3
равно 1)-1
2) 1
3) 5
4) -5
5) -3
Пусть А
 –
основная матрица системы линейных
алгебраических уравнений.
–
основная матрица системы линейных
алгебраических уравнений. –
расширенная матрица системы. Система
несовместна, если
–
расширенная матрица системы. Система
несовместна, если
1)
R(A)
= 4, R(![]() )=
4 2)
R(A)
= 3, R(
)=
4 2)
R(A)
= 3, R(![]() )=
3 3)
R(A)
= 4, R(
)=
3 3)
R(A)
= 4, R(![]() )=
3
)=
3
4)
R(A)
= 2, R(![]() )=
2
5) R(A)
= 2, R(
)=
2
5) R(A)
= 2, R(![]() )=
3
)=
3
Работа силы
 (3;
5; 1) при
перемещении материальной точки из
положения
(3;
5; 1) при
перемещении материальной точки из
положения
 в
в равна 1)38
2) 31
3) 27
4) 11
5) 14
равна 1)38
2) 31
3) 27
4) 11
5) 14
Векторное произведение
 векторов
векторов
 (0;
1; 3),
(0;
1; 3), (5;
-1; 8) равно
(5;
-1; 8) равно
1) (5;
0; 11) 2)
(11; -15; -5)
3)
![]() 4)
4)
![]() 5)(11; 15; -5)
5)(11; 15; -5)
Уравнение плоскости α, изображенной на рисунке, имеет вид
 α
1) x
– y + 2z + 3 = 0
α
1) x
– y + 2z + 3 = 0
2) –x – 2y + z – 3 = 0
![]() (-1;-2;1)
3)
(-1;-2;1)
3)
![]() +
+![]() +
z – 2 = 0
+
z – 2 = 0
4)
-![]() -
-![]() +
+![]() =
1
=
1
M0(1;-1;2) 5) –x – 2y + z + 3 = 0
У
 равнение
прямойl,
изображенной на рисунке имеет вид
равнение
прямойl,
изображенной на рисунке имеет вид
y
1350
0 4 х
-1 M0
1) y
= x
-3 2)
![]() 3) y
= - x
- 3 4) y
= - x
+ 3 5)
3) y
= - x
- 3 4) y
= - x
+ 3 5)
![]()
Координаты направляющего вектора прямой L:
 равны
равны
1) (-1;0;5)
2) (0;7;-3)
3)![]() 4)(-1;7;2)
5) (1;0;-5)
4)(-1;7;2)
5) (1;0;-5)
Среди уравнений кривых второго порядка указать уравнение параболы
1) y2+2(x-1)2
=3
2) y2
- x2
=1
3) y2
=4x+3
4) y2
=1-![]() 5) x2
=9 + y2
5) x2
=9 + y2
Вычислить

 и указать номер правильного ответа.
и указать номер правильного ответа.
1) 0
2) 3
3) -7
4)
![]() 5) -3
5) -3
Вычислить
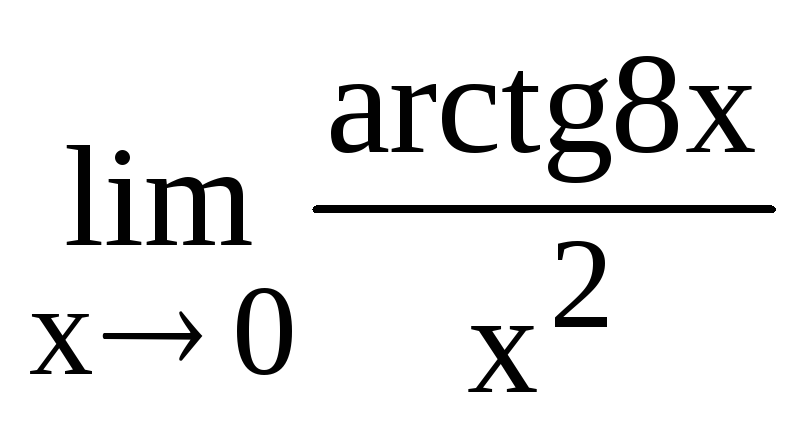 и указать номер правильного ответа.
и указать номер правильного ответа.
1) 8
2) 0
3) 64
4)
![]() 5)
5)
![]()
Угловой коэффициент нормали, проведённой к графику функции f(x)=2x+ex в точке с абсциссой x0=0, равен
1) -1
2)
![]() 3)
3)![]() 4) 0
5)
4) 0
5)
![]()
Найдите
 и укажите
номер правильного ответа, если y
=
и укажите
номер правильного ответа, если y
=
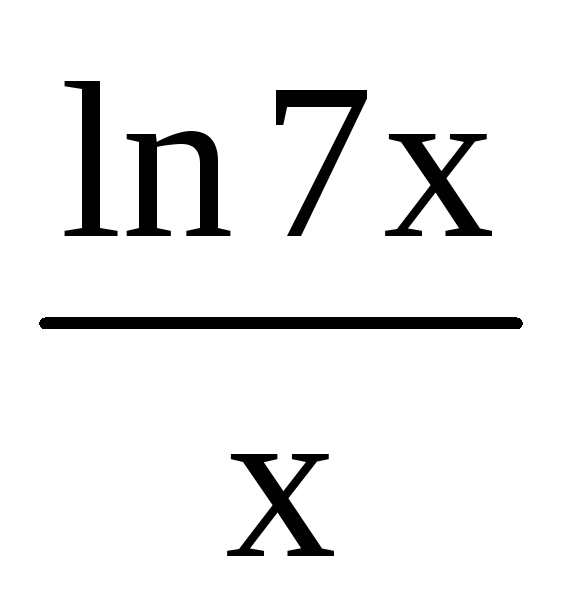 .
.
1)
![]() 2)
2)
![]() 3)
3)![]() 4)
4)
![]() 5)
5)
![]()
Приведите пример графика функции
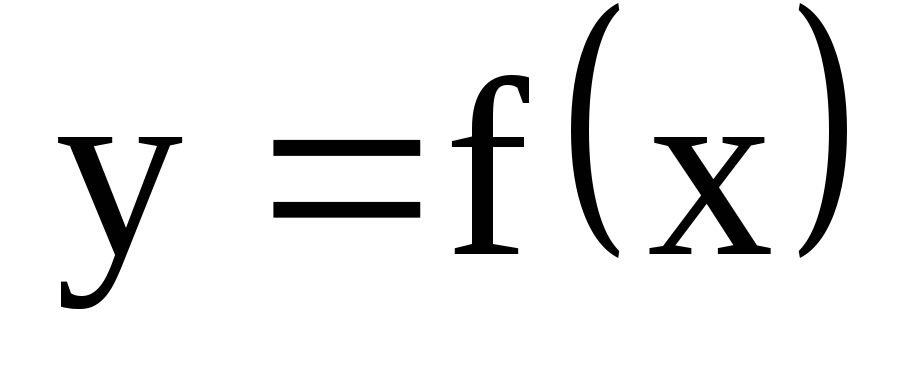 ,
удовлетворяющей условию
,
удовлетворяющей условию
Значение выражения (2i+3)(i-8)+i6 равно:
1) -27-13i 2) -5+3i 3) 40 4) -26-13i 5) 27+13i
Если z = 3x2y2+5y2x , то значение выражения
 равно
равно
1) 12x+10 2) 12xy+10y 3) 6x2y+10xy 4) 6x2y 5) 10xy
Интеграл
 равен
равен
1)
![]() 2)
2)![]() 3)arctgx
+ C
3)arctgx
+ C
4)
![]() 5)
5)![]()
Площадь фигуры, ограниченной линиями: y=x, y=
 ,x=2,
равна
,x=2,
равна
1) 2-ln2
2)
![]() +ln2
3)
+ln2
3)
![]() -ln2
4)
2+ln2
5)
2
-ln2
4)
2+ln2
5)
2
Масса неоднородной плоской пластины плотности
 ,
ограниченной линиямиy=x,
y=x2,
равна
,
ограниченной линиямиy=x,
y=x2,
равна
1) 1
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
10
5)
10
Общее решение (общий интеграл) уравнения
 имеет вид
имеет вид
1)
![]() 2) y=x
(x+ln|x|+C)
3) y=x2
+xln|x|
4)
2) y=x
(x+ln|x|+C)
3) y=x2
+xln|x|
4)
![]() 5)
5)
![]()
Частное решение с неопределенными коэффициентами – y* дифференциального уравнения y// -4y/+13y=5x2+1 равно
1) e2x(Acos3x+Bsin3x) 2) 5Ax2+B 3) Ax2+Bx 4) Ax2+Bx+C 5) e2x(Ax2 cos3x+Bxsin3x)
Среди рядов 1.
 2.
2. 3.
3. 4.
4. расходятся
расходятся
1) только 1 2) только 1 и 4 3) только 2
4) только 3 5) только 3 и 4
Четвёртый член разложения функции y=ln(x-4) в ряд Тейлора в окрестности точки х0=6 имеет вид
1)![]() 2)
2)![]() 3)
3)![]() 4) -
4) -![]() 5)
5)![]()
В группе 12 учащихся. Из них 5 юношей, остальные девушки. К доске вызываются двое учащихся. Вероятность того, что это девушки, равна
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Дан закон распределения дискретной случайной величины X:
|
xi |
1 |
2 |
3 |
5 |
|
pi |
0,1 |
0,3 |
0,4 |
0,2 |
Среднее квадратическое отклонение равно
1) 9,9
2)
![]() 3)2,9
3)2,9
4)![]() 5)
5)![]()
Если дифференциальная функция распределения непрерывной случайной величины X

то интегральная функция распределения вероятностей имеет вид
1)
 2)
2)
3)
 4)
4)
5)

