
Тест 11
Определитель матрицы
 ,
равен
,
равен
1) -11 2) 11 3) -9 4) 6 5) 9
Пусть
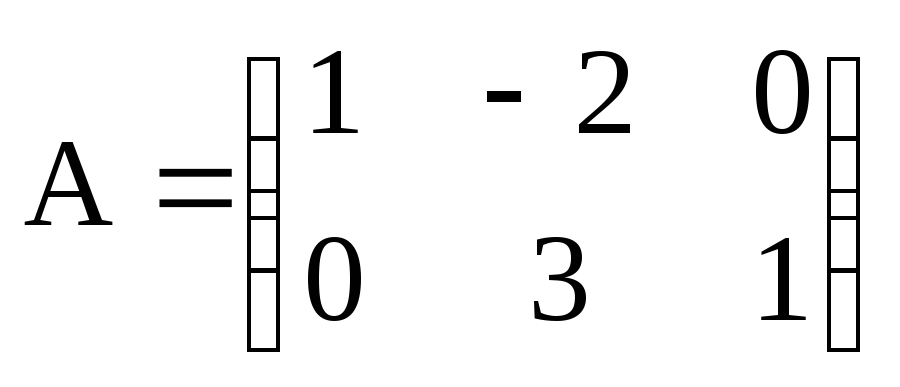 ,
, .
МатрицаС=А-3В
имеет вид
.
МатрицаС=А-3В
имеет вид
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Матрица
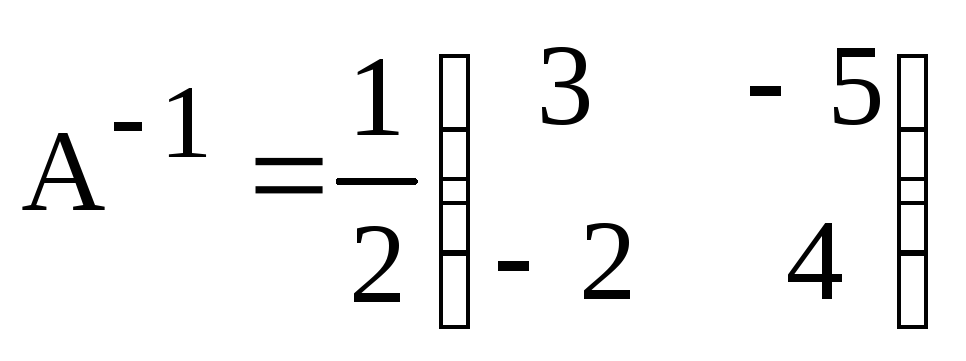 является обратной для матрицы
является обратной для матрицы
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Если (
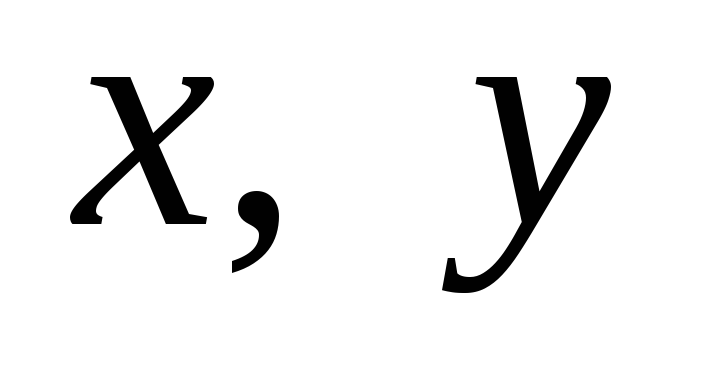 )
- решение системы линейных уравнений
)
- решение системы линейных уравнений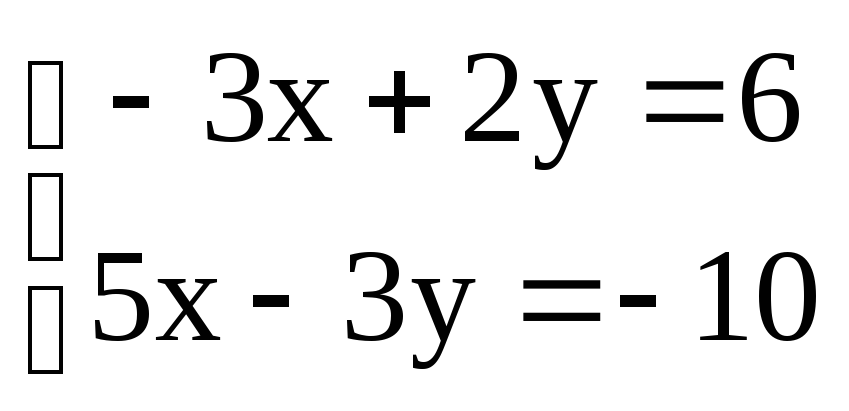 ,
то
,
то равно 1)-4
2) 4
3)
равно 1)-4
2) 4
3)
 4)-2
5) 1
4)-2
5) 1Пусть А33 – основная матрица системы линейных алгебраических уравнений. Ā - расширенная матрица. Система имеет единственное решение, если
1) R(A)=2, R(Ā)=2 2) R(A)=2, R(Ā)=3 3) R(A)=1, R(Ā)=1
4) R(A)=3, R(Ā)=4 5) R(A)=3, R(Ā)=3
Если
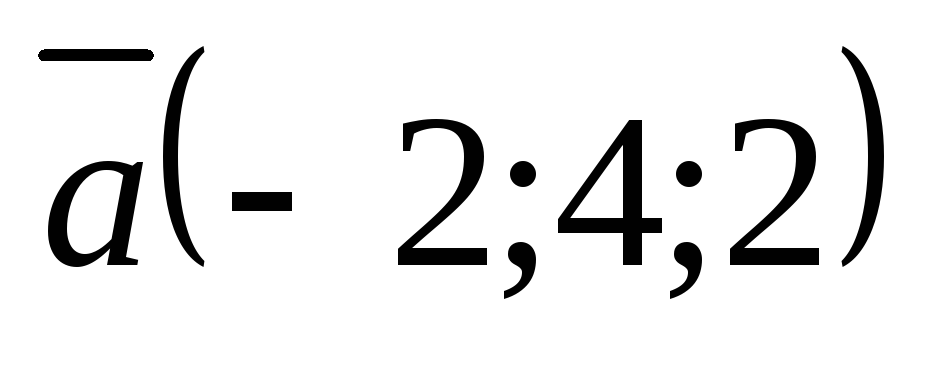 ,
, ,
, ,
то проекция вектора
,
то проекция вектора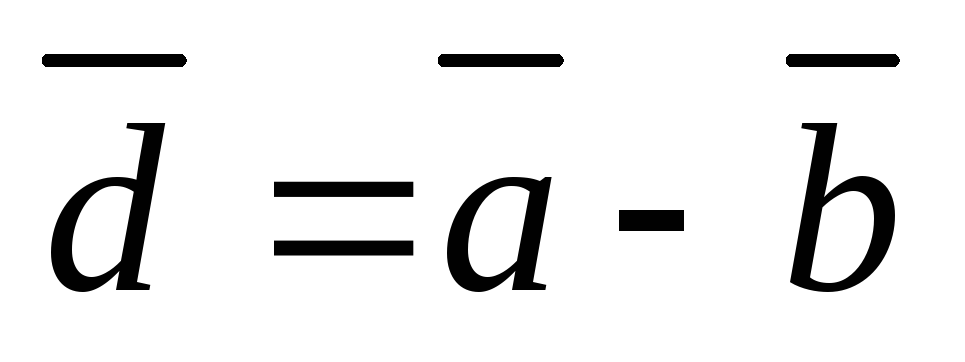 на вектор
на вектор равна
равна
1)
![]() 2)
2)![]() 3)
3)
![]() 4)
4)![]() 5)
5)
![]()
Векторное произведение
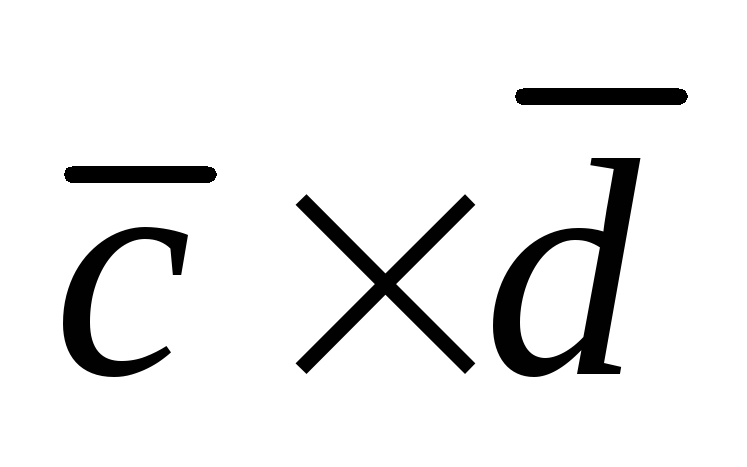 векторов
векторов
 (-4;
2; 0),
(-4;
2; 0), =
= +2
+2 ,
равно
,
равно
1) (4;
-8; -2) 2)
![]() 3)(-3; 2;
1) 4)
3)(-3; 2;
1) 4)
![]() 5)(4; 8; -2)
5)(4; 8; -2)
Уравнение плоскости a, изображенной на рисунке, имеет вид
1 )
)![]()
2)
![]()
3
0![]()
4)
![]()
5)
![]()
Уравнение прямой l, изображенной на рисунке, имеет вид

1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Координаты направляющего вектора прямой L:
 ,
равны
,
равны
1) (0;
-1; 2)
2)
![]() 3) (0; 1; 2)
4) (-3;
4; 3) 5) (-3;
5; 5)
3) (0; 1; 2)
4) (-3;
4; 3) 5) (-3;
5; 5)
Полуоси кривой второго порядка
 ,
равны
,
равны
1) a=3;
b=2
2) a=-1;
b=0
3) a=9;
b=4 4)
a=![]() ;
b=
;
b=![]() 5) a=
5) a=![]() ;
b=
;
b=![]()
Вычислить
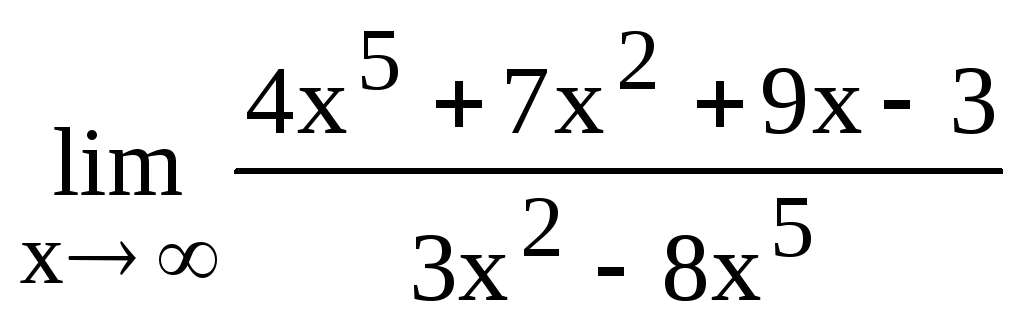 и указать номер правильного ответа.
и указать номер правильного ответа.
1)
![]() 2)-3
3) 0
4)
2)-3
3) 0
4)
![]() 5)
5)![]()
Вычислить
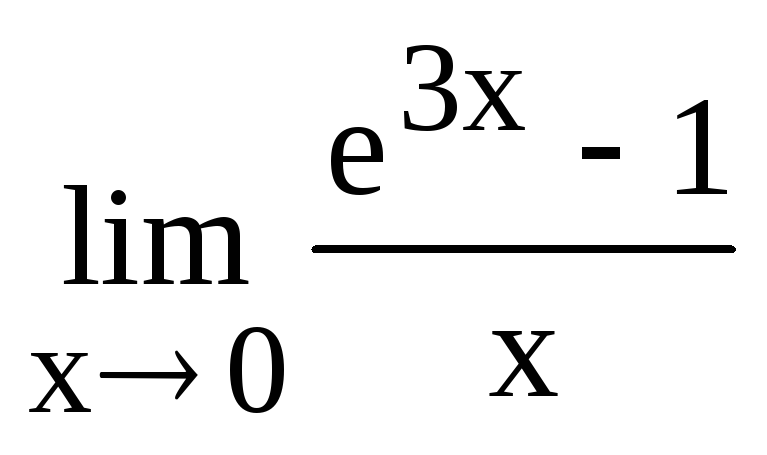 и указать номер правильного ответа.
и указать номер правильного ответа.
1)
![]() 2)0
3) 3
4)
2)0
3) 3
4)
![]() 5)e3
5)e3
Нормаль к графику функции
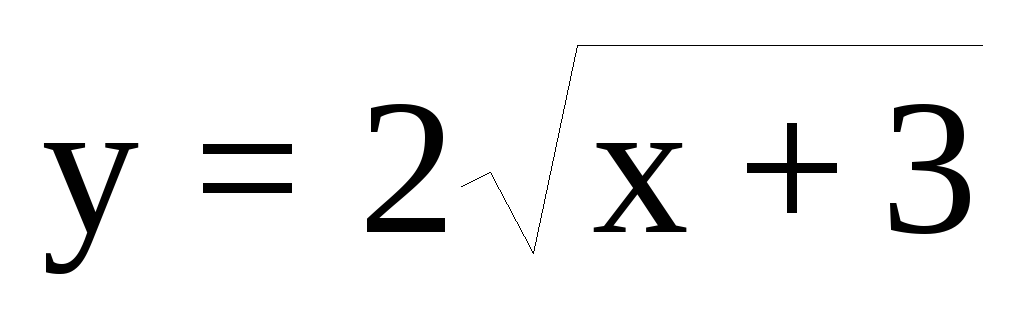 образует
с положительным направлением осиОХ
угол 1350,
если она проведена в точке с координатами
образует
с положительным направлением осиОХ
угол 1350,
если она проведена в точке с координатами
1) (1;4)
2) (-1;![]() )
3) (0;
)
3) (0;
![]() )
4) (1; -
)
4) (1; -![]() )
5) (-2;2)
)
5) (-2;2)
Если y =
 , то значение
dу , равно
, то значение
dу , равно
1)
 2)
2) 3)
3) 4)
4)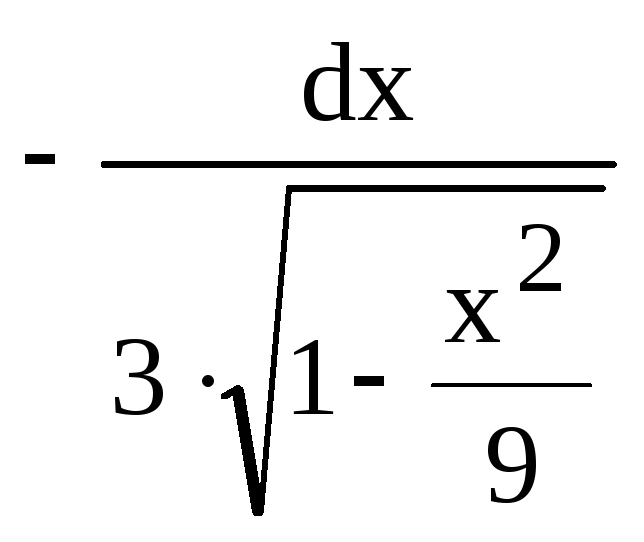 5)
5)![]()
Приведите пример графика функции
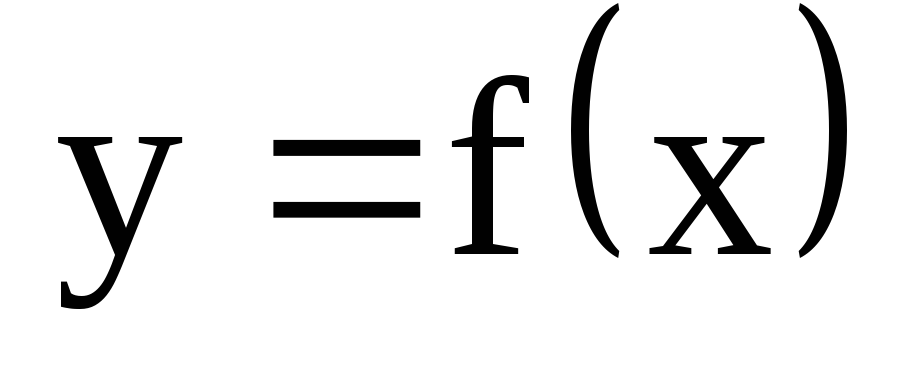 ,
удовлетворяющей условию
,
удовлетворяющей условию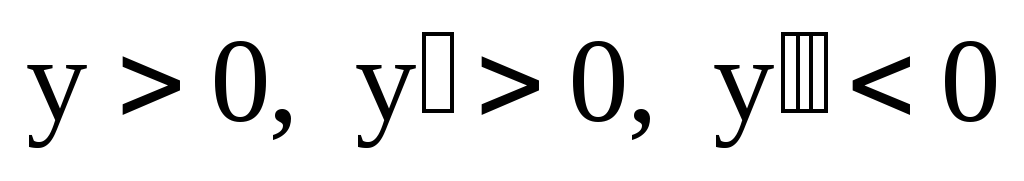
Значение выражения
 ,
равно
,
равно
1)
![]() 2)
2)![]() 3)-2
4)
3)-2
4)
![]() 5)1
5)1
Если
 ,
то значение выражения2z/x-z/y
, равно
,
то значение выражения2z/x-z/y
, равно
1) 4x+6y 2) 10x+6y 3) 4x+12y 4) 14x+12y 5) 14x-12y
Интеграл
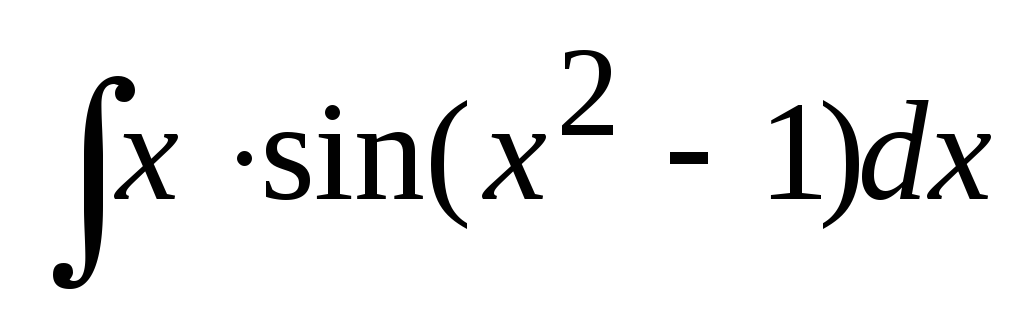 ,
равен
,
равен
1)![]() 2)
2)![]() +С
3)
+С
3)![]() +С
+С
4)
![]() +С
5)
+С
5)
![]() +С
+С
Площадь фигуры, ограниченной линиями
 ,
,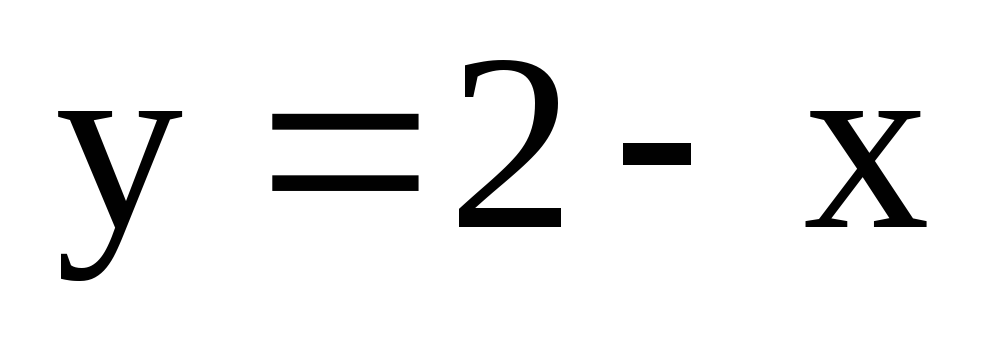 ,
,
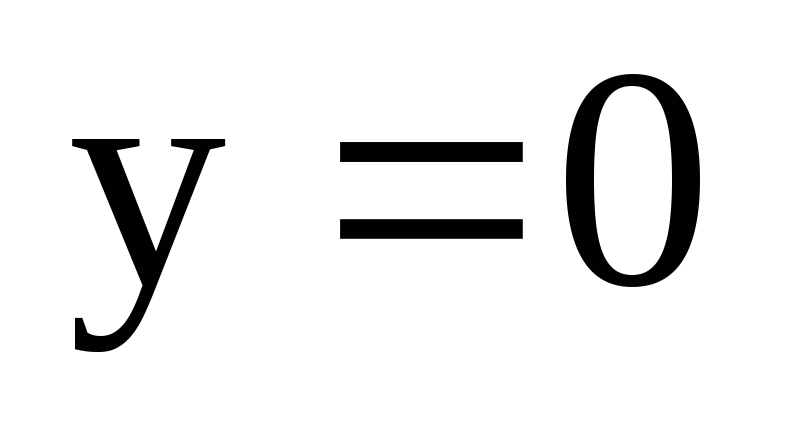 ,
равна
,
равна
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]() 5)
5)![]()
Масса однородного тела плотности
 ,
изображенного на рисунке, равна
,
изображенного на рисунке, равна
1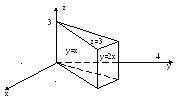 )13k
)13k
2) 16k
3) 12k
4
0
5) 24k

4

Общее решение (общий интеграл) уравнения
 ,
имеет вид
,
имеет вид
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)
![]() 5)
5)![]()
Частное решение с неопределенными коэффициентами – у* дифференциального уравнения y// + y = xcosx+2sinx, равно
1) Axcosx+2Bsinx 2) x(Acosx+Bsinx) 3) Acosx+Bsinx
4) ((Ax+B)cosx+Csinx)x 5) ((Ax+B)cosx+(Cx+D)sinx)x
Для исследования ряда
 на сходимость целесообразнее использовать
на сходимость целесообразнее использовать
1) Необходимый признак сходимости
2) Признак сравнения в предельной форме 3) Признак Д’Аламбера
4) Признак сравнения 5) Признак Лейбница
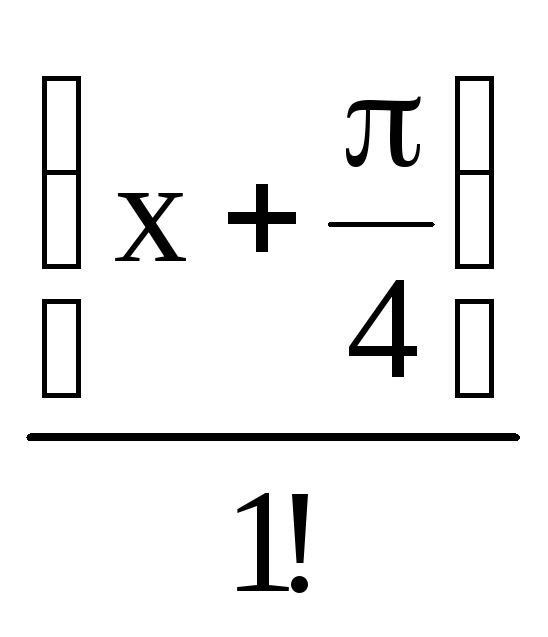
Второй член разложения функции y=sin2x в ряд Тэйлора в окрестности точки х0=
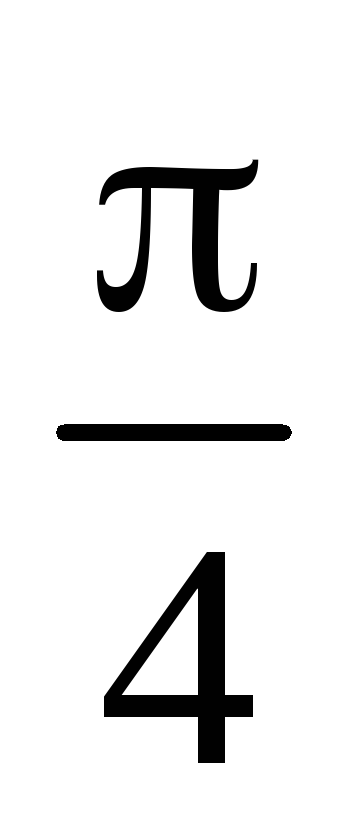 ,
имеет вид
,
имеет вид
1)
![]() 2)
2)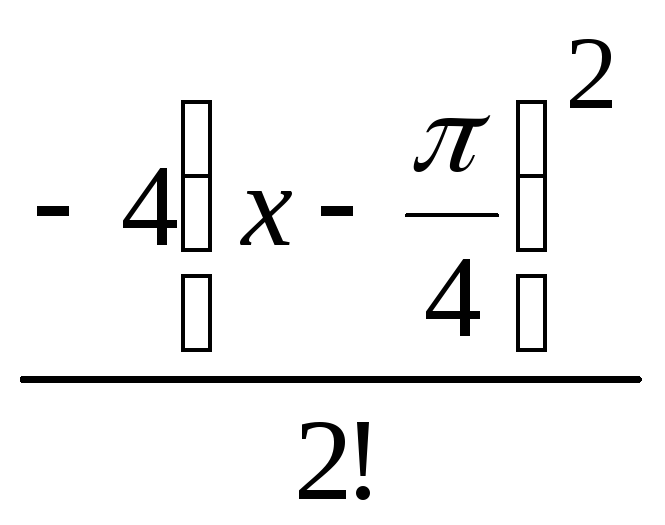 3)
3)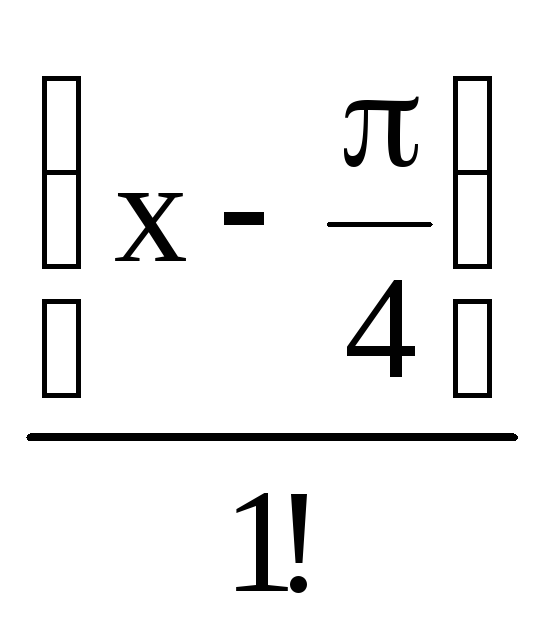 4)
4) 5)
5)
Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Вероятность того, что номер первого наудачу извлеченного жетона содержит цифру 5, равна 1) 0,8 2) 0,19 3) 0,1 4) 0,81 5) 0,9
Дан закон распределения дискретной случайной величины X:
|
xi |
-4 |
-2 |
2 |
4 |
|
рi |
0,6 |
0,1 |
0,2 |
0,1 |
Среднее квадратическое отклонение равно
1)
![]() 2)-12,4
3)
2)-12,4
3)
![]() 4)9,16
5)
4)9,16
5)
![]()
Математическое ожидание непрерывной случайной величины X, заданной функцией плотности распределения вероятностей

равно 1) 1
2) 0
3) 2,75
4)
![]() 5)2,5
5)2,5
