
Посібник ЧМ
.pdf
|
|
|
1.0 |
|
|
|
|
|
2.718 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.25 |
|
|
|
f X |
|
|
2.792 |
|
|
X |
1.5 |
i 0 4 |
y |
i |
y |
|
2.988 |
|
|
|
|
|
|
|
i |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
1.75 |
|
|
|
|
|
|
3.288 |
|
|
|
2.0 |
|
|
|
|
|
3.695 |
|
h X1 |
X0 |
0.25 |
|
|
|
|
|
|
|
|
Обчислимо праву, ліву та центральну різницеві похідні для точки x2 1.5:
P1_rigth |
y3 y2 |
1.202 |
P1_lefth |
y2 y1 |
0.782 |
P1_c entral |
y3 y1 |
0.992 |
||||
|
|
|
|
2 h |
|
|||||||
h |
h |
|||||||||||
|
|
|
|
|
|
|||||||
Визначимо фактичне значення похідної у вказаній точці і похибки наближених формул:
d f (x) |
ex |
ex |
|
|
|
ex |
|
|
ex |
f1(1.5) 0.996 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f1(x) |
|
|
|
x2 |
||||||||||
dx |
x |
|
|
x2 |
x |
|
|
|||||||||
E_rigth |
|
f1(1.5) P1_rigth |
|
0.206 |
|
|||||||||||
|
|
|
|
|
|
|||||||||||
E_left |
f1(1.5) P1_lefth |
0.214 |
|
|||||||||||||
E_central |
|
f1(1.5) P1_central |
|
0.0038 |
|
|||||||||||
|
|
|
||||||||||||||
Оцінимо похибки аналітично. Для цього треба визначити найбільше за модулем значення другої та третьої похідних на розрахункових інтервалах.
d2 |
|
ex |
|
2 ex |
|
2 ex |
f2(x) |
ex |
|
2 ex |
|
2 ex |
||||||
2f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
2 |
|
3 |
|
x |
2 |
|
3 |
|
|||||||||
dx |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
x |
|
|
|
|
x |
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
f2(1.25) 1.899 f2(1.5) 1.66 f2(1.75) 1.678
для правої різницевої похідної на інтервалі [x2; x3]
|
|
h |
|
|
|
||
_rigth |
|
|
f2(1.75) |
0.2097 |
|||
2 |
|||||||
|
|
|
|
|
|||
для лівої різницевої похідної на інтервалі [x1; x2]
|
|
|
|
|
|
|
|
_lefth |
|
h |
|
|
|
f2(1.5) |
|
0.2075 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||
d3 |
ex |
3 ex |
6 ex |
|
6 ex |
|
|
|
|
|
|
ex |
3 ex |
6 ex |
|
6 ex |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f3(x) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
dx |
x |
2 |
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
3 |
|
|
4 |
|
||
|
|
x |
x |
|
x |
|
|
|
|
|
|
|
|
|
|
x |
x |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
81

f3(1.25) 1.765 f3(1.75) 0.412
для центральної різницевої похідної на інтервалі [x1; x3]
|
|
h 2 |
|
|
|||
_central |
|
|
f3(1.25) |
0.0184 |
|||
6 |
|
||||||
|
|
|
|
|
|
||
Обчислимо другу похідну для точки x2 1.5 та похибку формули:
P2_central |
y3 2 y2 y1 |
1.681 |
|
|
f2(1.5) 1.66 |
|
|
|
|||||||||||
|
|
|
h 2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E2_central |
f2(1.5) P2_central |
0.0206 |
|
|
|
|
|
|
|||||||||||
|
d4 |
f (x) |
ex |
|
4 ex |
12 ex |
24 ex |
24 ex |
f4(x) |
d4 |
f (x) |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|||||||||||||
4 |
|
x |
2 |
|
|
3 |
|
4 |
|
5 |
|
|
|
||||||
|
dx |
|
|
|
|
|
|
|
dx |
|
|||||||||
|
|
|
|
|
x |
x |
x |
x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f4(1.25) 8.439
f4(1.75) 2.346
|
|
h 2 |
|
|
|
||
2_c entral |
|
|
f4(1.25) |
0.044 |
|||
12 |
|||||||
|
|
|
|
|
|||
2.Обчислити першу та другу похідні від заданої функції f(x) в точці x2 , використову-
ючи інтерполяційні поліноми. Оцінити похибку обчислень.
|
e x |
|
|
|
|
|
|
|
f (x) |
i |
0 |
1 |
2 |
3 |
4 |
||
|
, |
|
|
|
|
|
|
|
x |
xi |
1.0 |
1.25 |
1.5 |
1.75 |
2.0 |
||
Побудуємо інтерполяційний поліном Ньютона. Знайдемо поділені різниці:
f01 |
y1 |
y0 |
|
0.296 f12 |
y2 |
y1 |
0.782 |
f23 |
|
y3 y2 |
1.202 |
f34 |
y4 |
y3 |
1.625 |
|||||||||||||||
|
|
|
h |
|
|
h |
|
|
h |
|
|
|
|
h |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f012 |
f12 f01 |
0.972 |
|
f123 |
f23 f12 |
0.84 |
f234 |
f34 f23 |
0.845 |
|||||||||||||||||||||
|
|
2 h |
|
|
|
|
2 h |
|
2 h |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f0123 |
|
f123 f012 |
0.176 |
|
f1234 |
|
f234 f123 |
0.0064 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
3 h |
|
|
|
|
|
|
|
|
3 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
|
|
|
|

f01234 |
|
f1234 f0123 |
0.182 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1(x) x X f01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2(x) |
x2 |
x X |
X X X |
f012 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
N3(x) |
x3 |
x2 X |
|
|
X |
X x X X |
X X |
X X X X X |
f0123 |
|
|
|
|||||||||||||||||||||
|
|
0 |
|
|
1 |
2 |
|
|
0 |
1 |
|
0 |
2 |
|
1 |
2 |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
N4(x) x4 x3 X |
X X X |
x2 X X |
X X |
X X |
|
X X |
|
X X |
X X |
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
1 |
2 |
3 |
|
|
|
0 |
1 |
|
0 |
2 |
|
0 |
3 |
|
|
1 |
2 |
|
1 |
3 |
2 |
3 |
||||
N4(x) N4(x) x X |
X X |
X X X |
|
X X X |
X |
X X |
|
X |
X X X f01234 |
|
|||||||||||||||||||||||
|
|
|
|
0 |
1 |
2 |
0 |
1 |
3 |
|
|
0 |
2 |
3 |
|
1 |
2 |
3 |
|
|
|
0 |
|
1 |
|
2 |
3 |
|
|
|
|||
N(x) y0 N1(x) N2(x) N3(x) N4(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
N(1.5) 2.9878 |
|
|
|
f (1.5) N(1.5) |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Обчислимо значення першої похідної та її похибку:
NP1(x) f01
NP2(x) 2 x |
|
X |
X |
|
|
f012 |
|
|
|
|
|
|
|
|||
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
NP3(x) |
2 |
|
2 x X |
|
X |
X X X |
X X |
|
|
|
||||||
3 x |
X X f0123 |
|||||||||||||||
|
|
|
|
|
0 |
|
|
1 |
2 |
0 |
1 |
0 |
2 |
1 |
2 |
|
NP4(x) 4 x3 3x2 X0 X1 X2 X3 2x X0 X1 X0 X2 X0 X3 X1 X2 X1 X3 X2 X3
NP4(x) NP4(x) |
|
X X X |
X X X |
X X X |
X X X f01234 |
|||||||||
|
0 |
1 |
2 |
0 |
1 |
3 |
0 |
2 |
3 |
1 |
2 |
3 |
|
|
|
|
|||||||||||||
NP(x) NP1(x) NP2(x) NP3(x) NP4(x)
NP(1.5) 0.9974
_NP |
f1(1.5) NP(1.5) |
0.0015 |
Обчислимо значення другої похідної та її похибку:
NPP2(x) 2 f012
NPP3(x) 6 x |
2 |
X |
X |
X |
|
f0123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
NPP4(x) |
|
2 |
6x X |
|
X |
X |
X |
2 X X |
X X |
X X |
X X |
X X |
|
|
|
||||||||
12 x |
X X f01234 |
||||||||||||||||||||||
|
|
|
|
|
0 |
|
1 |
|
2 |
3 |
0 |
1 |
0 |
2 |
0 |
3 |
1 |
2 |
1 |
3 |
2 |
3 |
|
NPP(x) NPP2(x) NPP3(x) NPP4(x)
NPP(1.5) 1.6577
_NPP |
|
f2(1.5) NPP(1.5) |
|
0.0021 |
|
|
Тепер побудуємо інтерполяційний поліном Лагранжа.
|
|
( 1)4 y0 |
|
|
|
4 |
|
3 |
|
2 |
|
|
|
L0(q) |
0 4 |
|
|
|
q |
|
10q |
|
35q |
|
50q |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L1(q) |
|
( 1)3 y1 |
q4 |
9q3 26q2 |
24q |
|
|||||||
|
1 3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
L2(q) |
|
( 1)2 y2 |
q4 |
8q3 19q2 |
12q |
|
|||||||
|
2 2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
83

L3(q) |
( 1)1 y3 |
q4 |
7q3 |
14q2 |
8q |
||
3 1 |
|
||||||
|
|
|
|
|
|||
L4(q) |
( 1)0 y4 |
|
q4 |
6q3 |
11q2 |
6q |
|
4 0 |
|||||||
|
|
|
|
|
|||
L(q) L0(q) L1(q) L2(q) L3(q) L4(q)
q(x) |
x X0 |
q(1.5) 2 |
|
|
||
h |
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|||
L(q(1.5)) 2.9878 |
|
f (1.5) |
L(q(1.5)) |
0 |
||
Обчислимо значення першої похідної та її похибку:
|
|
|
( 1)4 y0 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|||||||||
LP0(q) |
|
|
0 4 |
|
|
|
|
4q |
|
|
|
30q |
|
|
70q |
50 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
( 1)3 y1 |
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||
LP1(q) |
1 3 |
|
|
|
|
4q |
|
27q |
|
52q |
24 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
( 1)2 y2 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||
LP2(q) |
|
|
|
|
|
|
|
4q |
|
|
|
24q |
|
|
38q |
12 |
|
|
|
|
||||||||
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( 1)1 y3 |
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|||||||
LP3(q) |
|
|
|
|
|
|
4q |
|
|
21q |
|
|
28q |
8 |
|
|
|
|
||||||||||
|
|
|
|
|
3 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
( 1)0 y4 |
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|||||||
LP4(q) |
|
|
|
|
|
|
4q |
|
|
18q |
|
|
22q |
6 |
|
|
|
|
||||||||||
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
LP(q) (LP0(q) LP1(q) LP2(q) LP3(q) LP4(q)) |
1 |
|||||||||||||||||||||||||||
h |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q(x) |
x X0 |
|
|
|
|
|
|
q(1.5) |
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
LP(q(1.5)) 0.9974 |
|
|
|
P |
|
f1(1.5) LP(q(1.5)) |
|
0.0015 |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
Обчислимо значення другої похідної та її похибку:
LPP0(q) ( 1)4 y0 12q2 60q 70 0 4
LPP1(q) ( 1)3 y1 12q2 54q 52 1 3
LPP2(q) ( 1)2 y2 12q2 48q 38 2 2
LPP3(q) ( 1)1 y3 12q2 42q 28 3 1
LPP4(q) ( 1)0 y4 12q2 36q 22 4 0
84

LPP(q) (LPP0(q) LPP1(q) LPP2(q) LPP3(q) LPP4(q)) 1
|
x X0 |
|
|
h 2 |
|
q(x) |
q(1.5) 2 |
|
|||
|
|
|
|||
h |
|
||||
|
|
|
|
||
|
|
|
|||
LPP(q(1.5)) 1.6577 |
PP |
f2(1.5) LPP(q(1.5)) |
0.0021 |
||
Як бачимо, |
значення інтерполяційних поліномів в заданій точці x2 1.5 співпали із |
||||
значенням функції, що говорить про правильність їх побудови. Однак, задачі чисельного диференціювання мають похибки, що свідчить про те, що наближене диференціювання являє собою операцію менш точну, ніж інтерполювання.
КОНТРОЛЬНІ ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ
1.Коли використовується чисельне диференціювання?
2.Приведіть найпростіші формули заміни першої та другої похідної різницями.
3.Як обчислити значення похідних за допомогою інтерполяційних поліномів?
4.Що ви можете сказати про точність задач чисельного диференціювання?
85

ТЕМА 9. Чисельне інтегрування
Лiтература: [2], пп. 2.1-2.5; [4], §§2.12-2.13; [5], п. 3.4; [6], гол. 8; [7], пп. 5.1-5.4
ТЕОРЕТИЧНІ ВІДОМОСТІ
Якщо функція f(x) – неперервна на відрізку [a,b] і відома її первісна функція F(x), то визначений інтеграл від цієї функції у границях від а до b може бути обчислений за формулою Ньютона-Лейбниця:
b |
|
|
|
I f (x)dx F (b) F (a), де |
(63) |
||
F (x) f(x). |
a
Але в багатьох випадках первісна функція F(x) не може бути знайдена, або є дуже складною. Крім того, підінтегральна функція f(x) може бути задана таблично, тоді поняття первісної функції взагалі втрачає сенс. Постає задача наближеного обчислення інтегралів за допомогою чисельних методів.
Усі чисельні методи обчислення інтегралів базуються на геометричній інтерпретації визначеного інтеграла, значення якого чисельно дорівнює площі фігури, що обмежена зверху – графіком функції f(x), знизу – віссю 0х, зліва та справа – межами інтегрування x=a, x=b (рис. 7). Для знаходження площі відрі-
зок [a,b] розбивають на n рівних частин довжиною h, де h b a . Значення n n
обирають, виходячи з умови задоволення точності обчислень. Значення інтеграла I шукають як суму елементарних площадей фігур, що побудовані на інтервалах [xi , xi h].
Рис.7
Метод лівих прямокутників. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами прямокутників, висота яких дорівнюватиме значенню f(x) у лівому кінці інтервалу [xi , xi h] (рис. 8). Загальну площу фігури обчислимо, як суму площ окремих
елементарних прямокутників:
86

|
|
Рис.8 |
|
|
|
|
n 1 |
b a n 1 |
b a n 1 |
|
|||
I Si |
|
yi |
|
f (xi ). |
(64) |
|
n |
n |
|||||
i 0 |
i 0 |
i 0 |
|
|||
Точність формули лівих прямокутників можна оцінити так:
|
(b a)2 |
|
|
|
|
|
f ( ), |
(65) |
|
2n |
||||
|
|
|
де [a,b] - точка, в якій перша похідна функції f(x) набуває найбільшого за модулем значення.
Метод правих прямокутників. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами прямокутників, висота яких дорівнюватиме значенню f(x) у правому кінці інтервалу [xi , xi h] (рис. 9). Загальну площу фігури обчислимо, як суму площ окремих
елементарних прямокутників:
|
|
Рис.9 |
|
|
|
|
n |
b a |
n |
b a |
n |
|
|
I Si |
|
yi |
|
f (xi ). |
(66) |
|
n |
n |
|||||
i 1 |
i 1 |
i 1 |
|
Точність формули правих прямокутників можна оцінити за формулою (65). Метод середніх прямокутників. Апроксимуємо площі елементарних кри-
волінійних трапецій, обмежених зверху графіком функції f(x), площами прямокутників, висота яких дорівнюватиме значенню f(x) у середині інтервалу
87
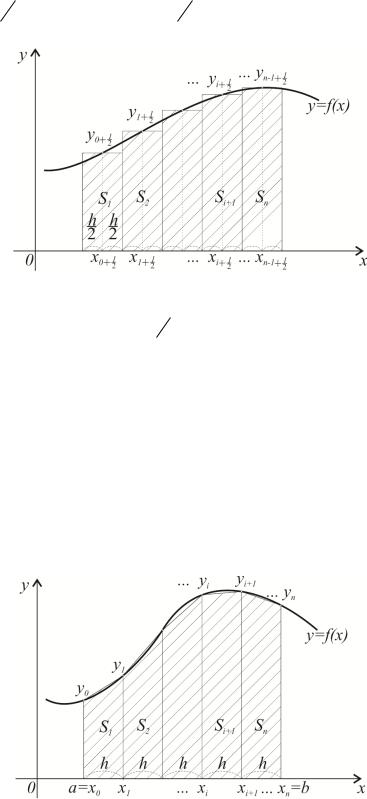
|
h] - y |
|
|
h |
|
|
|
|
|
|
[xi , xi |
1 |
f xi |
|
|
f x |
1 |
|
(рис. 10). Загальну площу фігури об- |
||
|
||||||||||
|
i |
2 |
|
2 |
|
i |
2 |
|
|
|
числимо, як суму площ окремих елементарних прямокутників:
|
|
|
|
Рис.10 |
|
|
|
||
n 1 |
b a n 1 |
|
|
b a n 1 |
h |
|
|
||
I Si |
|
y |
i |
1 |
|
f (xi |
|
). |
(67) |
|
|
|
|||||||
i 0 |
n i 0 |
2 |
n i 0 |
2 |
|
|
|||
|
|
|
|||||||
Точність формули середніх прямокутників можна оцінити так:
|
(b a)3 |
|
(68) |
|
|||
24n2 |
f ( ), |
||
|
|
|
де [a,b] - точка, в якій друга похідна функції f(x) набуває найбільшого за модулем значення.
Метод трапецій. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами трапецій, висота яких дорівнюватиме h, а довжини основ значенням f(x) у правому й лівому кінцях інтервалу [xi , xi h] - f (xi ) й f (xi h) (рис. 11). Загальну площу фігури обчи-
слимо, як суму площ окремих елементарних трапецій:
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
n 1 |
b a y |
|
|
y |
|
|
|
|||
I Si |
0 |
y1 ... yn 1 |
n |
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
i 0 |
n |
2 |
|
2 |
|
|||||
88

|
b a |
|
f (x0 ) |
f (x ) ... f (x |
n 1 |
) |
f (xn ) |
. |
(69) |
|
|
|
|||||||
|
|
|
2 |
1 |
|
|
|
||
|
n |
|
|
|
2 |
|
|||
Точність формули трапецій можна оцінити так:
|
(b a)3 |
|
(70) |
|
|||
12n2 |
f ( ), |
||
|
|
|
де [a,b] - точка, в якій друга похідна функції f(x) набуває найбільшого за модулем значення.
Метод Симпсона. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами криволінійних трапецій, обмежених зверху параболою, що проходить через три точки (x2i , y2i ) ,
(x2i 1, y2i 1) , (x2i 2 , y2i 2 ) , i 0,1,...,n (рис. 12). Кількість точок для формули Симпсона має бути завжди парною - n 2m . Загальну площу фігури обчислимо, як суму площ окремих елементарних криволінійних трапецій:
Рис.12
|
|
n 1 |
|
b a |
( y0 y2m ) 4( y1 y3 ... y2m 1) 2( y2 y4 ... y2m 2 ) |
|||||||||
|
I Si |
|||||||||||||
|
||||||||||||||
|
|
i 0 |
|
3n |
|
|
|
|
|
|
|
|
||
|
h |
f (x |
) f (x |
) 4 f (x ) ... f (x |
|
) 2 f (x |
|
) ... f (x |
|
) |
(71) |
|||
|
2m 1 |
2 |
2m 2 |
|||||||||||
3 |
0 |
|
2m |
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Точність формули Симпсона можна оцінити так:
|
(b a)5 |
f IV ( ), |
(72) |
|
180n4 |
||||
|
|
|
де [a,b] - точка, в якій четверта похідна функції f(x) набуває найбільшого за модулем значення.
ЗАВДАННЯ
1.Методами прямокутників, трапецій та Симпсона обчислити значення інтеграла з точністю 10 3 . Значення n обрати з умови задоволення точності розрахунків.
89

1. |
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cosxdx |
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
1,6 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
1 x |
|
|
|
|
|
|||||||||||||||
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 x4 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
dx |
|||||||||||
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x3arctg(x)dx |
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
0,5 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
cos x |
dx |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
6 |
|
|
|
|
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. |
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x10 sin xdx |
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 x3 dx |
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
x |
dx |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
|
|
|
||||||||||||||||
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10. |
1,0 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x4 |
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
11. |
13 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 1 x2 |
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|||||||||||||||
12. |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x2dx |
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x2dx |
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
1,2 |
|
|
cos x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dx |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x2 1 |
|
|
|
|
|
|||||||||||||
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
1,2 |
|
|
cos x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
dx |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
x 2 1 |
|
|
|
|
|
||||||||||||||
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16. |
0,6 |
|
|
|
|
|
|
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 x4 |
||||||||||||||
17. |
0 |
|
|
|
|
|
||||||||||||
e x2 dx |
||||||||||||||||||
|
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0,1 |
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18. |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 x3dx |
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
1,0 |
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
e |
dx |
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
20. |
0 ,25 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
e x2 dx |
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21. |
0,5 |
|
|
|
|
|
dx |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 x |
4 |
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
22. |
0,2 |
|
|
x |
|
|
|
|
|
|||||||||
|
|
e |
dx |
|||||||||||||||
|
3 |
|||||||||||||||||
|
0,1 |
|
x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
23. |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
cos x |
dx |
|||||||||||||||
|
|
|
x |
|||||||||||||||
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24. |
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x sin xdx |
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25. |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dx |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 x3 |
||||||||||||||
|
0 |
|
|
|
|
|
||||||||||||
26. |
|
2 sin x |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x |
dx |
||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
27.1,0

 x cos xdx
x cos xdx
|
0 |
|
|
|
|
|
|
28. |
1,6 |
sin(2x 2,1)dx |
|||||
|
|
||||||
|
|
|
x2 1 |
|
|||
|
1,2 |
|
|
|
|
|
|
29. |
1,0 |
|
|
|
|
|
|
|
|
|
|
x 1 |
cos x2dx |
||
|
0,2 |
|
|
|
|
|
|
30. |
1,2 |
tgx2 |
|||||
|
|
|
|
dx |
|||
|
|
x 1 |
|||||
|
0,5 |
|
|
|
|
|
|
90
