Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Посібник ЧМ

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

4.07 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

ТЕМА 2. Ітераційні методи розв’язування систем лінійних алгебраїчних рівнянь

Лiтература: [1], пп. 5.7-5.11; [3], §§2.8-2.10; [4], §1.6; [5], п. 1.1.4; [6], гол. 3

ТЕОРЕТИЧНІ ВІДОМОСТІ

Ітераційні методи використовують зазвичай для систем великої вимірності ( n 100 ), коли використання прямих методів є недоцільним через необхідність виконувати занадто велику кількість арифметичних операцій. Прямі методи дозволяють отримати точний розв’язок, але він не може бути досягнутий через накопичення похибок заокруглень при виконанні арифметичних операцій. Отриманий розв’язок може значно відрізнятися від точного. Ітераційними методами в таких випадках отримують розв’язки з більшою точністю ніж прямі.

Ітераційні методи передбачають побудову обчислювального (ітераційного) процесу, який дозволяє отримати послідовності наближень (ітерацій) розв’язку СЛАР, починаючи з деякого довільного наближення:

	x (0)				x (1)				x (2)				x (s)
(0)		1		(1)		1		(2)		1		(s)		1
		(0)				(1)				(2)				(s)
	x2				x2				x2				x2
x	...		, x		...		,	x	...		, …,	x	...		, які збігаються до то-
		(0)				(1)				(2)				(s)
	xn				xn				xn				xn

чного lim x			(s) x .
	s

Розглянемо систему лінійних алгебраїчних рівнянь із n-невідомими:

a11x1

a12 x2

a13 x3

... a1n xn b1,

a21x1

a22 x2

a23 x3

... a2n xn b2 , ,

(16)

...............................................

... a

n1 1

n3 3

...

де A a21

a22 ...

a2n

- матриця коефіцієнтів системи;

- вектор

...

... ...

...

an1

an2 ...

ann

- вектор невідомих.

вільних членів; x

...

Для побудови ітераційного процесу систему (16) приведемо до вигляду:

x1	1	11x1	12 x2	13 x3 ...		1n xn ,
x2	2	21x1	22 x2	23 x3	...	2n xn ,
x3	3	31x1	32 x2	23 x3	...	3n xn ,
......................................................................
xn	n	n1x1	n2 x2	n3 x3	...	n,n 1xn 1

, (17)

напри-

або x

x . Така система називається зведеною, її можна отримати,

клад, якщо кожне i-рівняння системи (16) розв’язати відносно змінної xi :

a12

a13

...

a1n

a11

a21

a23

a2n

...

a22

...

xn ,

a33

......................................................................................

an1

an2

an3

...

ann 1

n 1

ann

aij

i j; якщо i j, то

Тоді:

;

i, j 1,2,...,n;

(18)

aii

При побудові ітерацій постають питання про початок і кінець процесу обчислень. Будь який ітераційний процес починається з того, що задається початкове наближення. Як правило припускають, що

	(0) 0, або		(0)		(19)
x		x		.

Так як наближений розв’язок шукається з наперед заданою точністю , то послідовність повинна мати скінчену кількість членів, які отримуються за скінчену кількість ітерацій.

Найпростіша умова закінчення ітераційного процесу:

		x(s)	.	(20)
max	x(s 1)	x(s)	.	(20)
1 i n	i	i
1 i n

Тобто, обчислення продовжують до тих пір, доки абсолютна величина різниці між попереднім й наступним наближеннями не стане менше деякої наперед заданої точності :

Для дослідження збіжності ітераційного процесу користуються теоремою про достатню умову збіжності:

Якщо для зведеної системи (17) будь-яка канонічна норма матриці менше одиниці 1, то ітераційний процес збігається до єдиного розв’язку цієї

системи, незалежно від вибору початкового наближення.

Нормою матриці називається дійсне число , що задовольняє певним умовам, найбільш важливі з яких такі:

- 0, причому =0 тільки коли - нульова матриця;

-с с , де с – дійсне число с R.

Норма називається канонічною, якщо ij , тобто вона не менше мо-

дуля будь-якого елементу матриці .

На практиці зазвичай користуються трьома канонічними нормами:

max

- додаються за модулем всі рядки матриці і максима-

льна сума обирається нормою;

max

- додаються за модулем всі стовпці матриці і максима-

льна сума обирається нормою;

2 - додаються квадрати всіх елементів матриці і корінь з

i, j

цієї суми буде нормою.

Умова збіжності по відношенню до матриці А початкової системи (16) набуває такого змісту: процес ітерації буде збіжним, якщо модулі діагональних елементів матриці А будуть більші за суму модулів її сторонніх елементів (в рядку або стовпці):

	n				n
aii		aij	або	a jj		aij	(i, j 1,2,...,n) .	(21)
aii		aij	або	a jj		aij	(i, j 1,2,...,n) .	(21)
	j 1,				i 1,
	j i				i j

Виконання цих умов можна досягти, якщо застосувати правила лінійного комбінування рівнянь системи.

Метод простої ітерації. Кожне наступне наближення і-ой невідомої xi(s 1) ,

і=1,2,…, n визначається за допомогою системи рівнянь (11), в яких всі доданки правої частини беруться з попередній s-ітерації:

x	(s 1)													x		2			(s)				x (s) ...
1		1									12					2				13				3
x	(s 1)				2			21		x (s)											23			x	(s) ...
	2				2			21		1											23			3
x	(s 1)			3			31		x (s)				32				x			(s)					...
3				3			31			1			32							2
......................................................................
x	(s 1)		n					x		(s)		n2			x					(s)				x	(s) ...
	n		n			n1 1						n2						2				n3 3

Або система (10) в компактній формі:

	x		(s) ,
1n		n (s)
2n xn(s)				,
3n xn				,

(s)
n,n 1xn 1	.

xi(s 1)	n
xi(s 1)	i ij x(js) ;	i 1,2,...,n;	s 0,1,2,...

j 1 j i

(22)

(23)

Метод Зейделя являє собою деяку модифікацію метода простої ітерації. А саме, при обчисленні (s+1)-ого наближення невідомої xi враховуються вже об-

числені раніше значення невідомих на поточній ітерації x1(s 1) , x2(s 1) ,..., xi(s1 1) :

x	(s 1)									x			2		(s) x (s)
1		1								12			2			13			3
x	(s 1)				2			x (s 1)									23	x		(s)
	2				2		21		1								23		3
x	(s 1)			3		31		x	(s 1)		32	x			(s 1)
3				3		31		1			32			2
......................................................................
x	(s 1)		n				x		(s 1)		n2	x			(s 1)				n3	x
	n		n			n1 1					n2			2					n3	3

...

(s 1)

	x	(s) ,
1n		n (s)
2n xn (s)				,
3n xn				,	(24)
(s 1)
(s 1)
... n,n 1xn 1			.

або

	i 1	n
xi(s 1)	i ij x(js 1)	ij x(js) ;i 1,2,...,n;	s 0,1,2,...	(25)
	j 1	j i 1

ЗАВДАННЯ

1.Розв’язати СЛАР методами простої ітерації та Зейделя з точністю 0,001. Порівняти швидкість збіжності обох методів.

1,24 0,04x2

0,21x3

0,18x4

0,88 0,45x1

0,23x3

0,06x4

0,62 0,26x

0,34x

0,11x

1,17 0,05x

0,26x

0,34x

0,64 0,12x2

0,34x3

0,16x4

1,42 0,34x

0,17x

0,18x

0,42 0,16x

0,34x

0,31x

0,83 0,12x

0,26x

0,08x

1,83 0,18x2 0,02x3

0,21x4

0,65 0,16x1

0,14x3

0,27x4

2,23 0,37x

0,27x

0,24x

1,13 0,12x

0,21x

0,18x

0,04 0,42x2

0,32x3

0,03x4

1,42 0,11x1 0,26x3

0,36x4

0,83 0,12x

0,08x

0,24x

1,42 0,15x1

0,35x2

0,18x

1,33 0,34x2

0,12x3

0,15x4

0,84 0,11x1

0,15x3

0,32x4

1,16 0,05x

0,12x

0,18x

0,57 0,12x

1 0,08x

2 0,06x

2,13 0,23x2

0,44x3

0,05x4

0,18 0,24x1

0,31x3

0,15x4

1,44 0,06x

0,15x

0,23x

2,42 0,72x

0,08x

0,05x

1,71 0,31x2

0,18x3

0,22x4

0,62 0,21x1

0,33x3

0,22x4

0,89 0,32x

0,18x

0,19x

0,94 0,12x

0,28x

0,14x

1,21 0,27x2

0,22x3

0,18x4

0,33 0,21x

0,45x

0,18x

0,48 0,12x1

0,13x

0,18x

0,17 0,33x1

0,05x2

0,06x4

0,81 0,07x2

0,38x3

0,21x4

0,64 0,22x1

0,11x3

0,33x4

1,71 0,51x 0,07x

0,11x

1,21 0,33x

0,41x

2,7 0,22x2 0,11x3

0,31x4

1,5 0,38x1

0,12x3

0,22x4

10.

1,2 0,11x 0,23x

0,51x

0,17 0,17x

0,21x

0,31x

1,42 0,23x2

0,18x3

0,17x4

0,83 0,12x

0,08x

0,09x

16.

1,21 0,16x

0,24x

0,35x

0,65 0,23x

0,08x

0,05x

1,42 0.21x2

0,06x3

0,34x4

0,57 0,05x1

0,32x3

0,12x4

17.

0,68 0,35x

0,27x

0,05x

2,14 0,12x

0,43x

0,04x

1,42 0,27x2

0,13x3

0,11x4

0,48 0,13x1

0,09x3

0,06x4

18.

2,34 0,11x

0,05x

0,12x

0,72 0,13x

0,18x

0.24x

0,48 0,05x2 0,08x3

0,14x4

1,24 0,32x

0,12x

0,11x

19.

1,15 0,17x 1 0,06x

0,12x4

0,88 0,21x 0,16x

0,36x

0,21 0,28x2

0,17x3

0,06x4

1,17 0,52x

0,12x

0,17x

20.

0,81 0,17x1 0,18x

3 0,21x4

0,72 0,11x

0,22x

0,03x

0,22 0,52x2 0,08x3

0,13x4

1,8 0,07x1

0,05x3

0,41x4

21.

1,3 0,04x

0,42x

0,07x

0,33 0,17x1

0,18x

0,13x

1,3 0,02x2

0,62x3

0,08x4

1,1 0,28x1 0,33x3

0,07x4

22.

1,7 0,09x

0,13x

0,28x

1,5 0,19x

0,23x

0,8x

1,2 0,17x2

0,33x3

0,18x4

0,33 0,18x

0,43x

0,08x

23.

0,48 0,22x1

0,18x3

0,07x4

1,2 0,08x1

0,07x2

0,21x4

0,43 0,05x2

0,22x3

0,33x4

1,8 0,22x

0,08x

0,07x

24.

0,8 0,33x1

0,13x

0,05x

1,7 0,08x

0,17x

0,29x

0,11 0,22x2

0,33x3

0,07x4

0,33 0,45x1 0,23x3

0,07x4

25.

0,85 0,11x

0,08x

0,18x

1,7 0,08x

0,09x

0,33x

0,51 0,08x2

0,11x3

0,18x4

2,42 0,16x2

0,08x3

0,15x4

1,17 0,18x1 0,52x3 0,21x4

1,43 0,16x1

0,11x3

0,21x4

11. x

1,02 0,13x

0,31x

0,21x

26. x

0,16 0,05x 0,08x

0,34x

1,62 0,12x

0,28 0,08x

0,33x

0,28x

0,14x

0,18x

2,17 0,06x2

0,12x3

0,14x4

1,34 0,08x2

0,23x3

0,32x4

1,4 0,04x1 0,08x3

0,11x4

2,33 0,16x1

0,18x3

0,16x4

12.

2,1 0,34x

0,08x

0,14x

27.

0,34 0,15x

0,12x

0,18x

0,12x

0,03x

0,8 0,11x

0,63 0,25x

0,21x

0,16x

1,2 0,08x2

0,03x3

0,04x4

2,43 0,18x2

0,33x3

0,16x4

0,81 0,31x2

0,27x3

0,08x4

1,12 0,32x1

0,23x3

0,05x4

13.

0,92 0,33x

0,07x

0,21x

28.

0,43 0,16x

0,08x

0,12x

0,17 0,11x

0,03x

0,58x

0,83 0,09x

0,22x

0.13x

1,24 0,23x2

0,25x3

0,16x4

1,42 0,34x2

0,23x3

0,06x4

0,89 0,14x1

0,18x3

0,24x4

0,66 0,11x1

0,18x3

0,36x4

14.

1,15 0,33x

0,03x

0,32x

29.

1,08 0,23x

0,12x

0,35x

0,12x

0,57 0,12x

0,05x

0,15x

1,72 0,12x

0,47x

1,21 0,14x2

0,06x3

0,12x4

0,67 0,23x2

0,11x3

0,06x4

0,72 0,12x

0,32x

0,18x

0,88 0,18x

0,12x

0,33x

15.

0,58 0,08x1

0,12x

0,32x4

30.

0,18 0,12x1

0,32x3

0,07x4

1,56 0,25x

1,44 0,05x

0,22x

0,14x

0,11x

0,09x

ПРИКЛАД РОЗРАХУНКІВ

1.Розв’язати СЛАР методами простої ітерації та Зейделя з точністю 0,001. Порів-

няти швидкість збіжності обох методів.

x1 2,15 0,05x2 0,11x3 0,08x4,

x2 0,83 0,11x1 0,28x3 0,06x4,x3 1,16 0,08x1 0,15x2 0,12x4 ,x4 0,44 0,21x1 0,13x2 0,27x3.

Сформуємо матрицю коефіцієнтів системи та вектор вільних членів :

ORIGIN 1

	0	0.05	0.11	0.08		2.15

0.11		0	0.28	0.06	0.83
	0.08	0.15	0	0.12		1.16
	0.08	0.15	0	0.12		1.16

0.21		0.13	0.27	0		0.44

Перевіримо виконання умови збіжності ітераційного процесу для заданої системи. Знайдемо норми матриці :

перша норма


	4				4					4				4
1		1 j	0.24	2			2 j	0.45	3		3 j	0.35	4		4 j	0.61
1		1 j	0.24	2			2 j	0.45	3		3 j	0.35	4		4 j	0.61
	j 1				j 1					j 1				j 1
max( 1 2 3 4) 0.61						1 0,61<1.
max( 1 2 3 4) 0.61

друга норма

	4				4				4				4
1		i 1	0.4	2		i 2	0.33	3		i 3	0.66	4		i 4	0.26
1		i 1	0.4	2		i 2	0.33	3		i 3	0.66	4		i 4	0.26
	i 1				i 1				i 1				i 1

max( 1 2 3 4) 0.66

0,66 <1.

третя норма

i j 2 0.54065

0,54 <1.

i 1

j 1

Всі норми вийшли менше одиниці, умова збіжності ітераційного процесу для заданої зведеної СЛАР виконується.

Метод простої ітерації

Оберемо початкове наближення розв’язку:

2.15

0.83 x0 1.160.44

Будуємо послідовність розв’язків, контролюючи виконання досягнення заданої точності :

					2.2839
x1 x0		x1		0.9447
x1 x0		x1			1.5093
					1.5093

				0.4326
			2.3979
x2 x1	x2		0.9754			x1 x2			0.1967
			0.9754
			1.4325
			1.4325

			0.5699
			2.4019
x3 x2	x3		0.9331			x2 x3			0.0432
x3 x2	x3		1.4297



			0.5771
					2.4001
x4 x3		x4		0.9315			x3 x4		0.0091
x4 x3		x4			1.4229



					0.5717
					2.3988
x5 x4		x5			0.9301		x4	x5	0.0031
					0.9301
					1.4231
					1.4231

					0.5693
					2.3986
x6 x5		x6			0.9304		x5	x6	0.0006 < Задана точність досягнута!
					0.9304
					1.4231
					1.4231

					0.5689
		2.399
Відповідь: x	0.93
Відповідь: x		1.423 , кількість ітерацій k=6.
		1.423 , кількість ітерацій k=6.

		0.569

Метод Зейделя

2.15

0.83

Початкове наближення: x0

1.160.44

Будуємо послідовність розв’язків, контролюючи виконання досягнення заданої точності :

x11 1 j 1

x13 3 j 1

2.2839

0.93 x1 1.535

0.575

x21 1 j 1

x23 3 j 1

2.4113

0.9601 x2 1.4279

0.5767

x31 1 j 1

x33 3 j 1

2.4012

0.9311 x3 1.4226

0.5694

x41 1 j 1

x43 3 j 1

2.3986

0.9303 x4 1.4231

0.5689

1 j x0j
3 j x1j	4	3 j x0j
3 j x1j		3 j x0j
	j 3

1 j x1j
3 j x2j	4	3 j x1j
3 j x2j		3 j x1j
	j 3

x2 x1 0.1692

1 j x2j
3 j x3j	4	3 j x2j
3 j x3j		3 j x2j
	j 3

x3 x2 0.032

1 j x3j
3 j x4j	4	3 j x3j
3 j x4j		3 j x3j
	j 3

x4 x3 0.0028

			4	2 j x0j
x12 2 2 1 x11				2 j x0j
			j 2
	3	4 j x1j 4 4 x04
x14 4		4 j x1j 4 4 x04

j 1

			4	2 j x1j
x22 2 2 1 x21				2 j x1j
			j 2
	3	4 j x2j 4 4 x14
x24 4		4 j x2j 4 4 x14

j 1

			4	2 j x2j
x32 2 2 1 x31				2 j x2j
			j 2
	3	4 j x3j 4 4 x24
x34 4		4 j x3j 4 4 x24

j 1

			4	2 j x3j
x42 2 2 1 x41				2 j x3j
			j 2
	3	4 j x4j 4 4 x34
x44 4		4 j x4j 4 4 x34

j 1

x51 1 j 1

x53 3 j 1

2.3986

0.9305 x5 1.4232

0.5689

Відповідь: x

1 j x4j						4	2 j x4j
1 j x4j			x52 2 2 1 x51				2 j x4j
						j 2
3 j x5j	4	3 j x4j		3	4 j x5j 4 4 x44
3 j x5j		3 j x4j	x54 4		4 j x5j 4 4 x44
	j 3			j 1

x5 x4 0.0002 < Задана точність досягнута!

2.3990.93

, кількість ітерацій k=5.

1.4230.569

Швидкість збіжності метода Зейделя виявилася більшою на одну ітерацію, ніж швидкість метода простої ітерації.

КОНТРОЛЬНІ ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

1.На які дві групи поділяються методи розв’язання СЛАР?

2.Сутність ітераційних методів?

3.Яка умова закінчення ітераційного процесу?

4.Як перевірити збіжність ітераційних методів?

5.Чим відрізняється метод простої ітерації від методу Зейделя?

ТЕМА 3. Методи визначення коренів нелінійних рівнянь

Лiтература: [1], пп. 4.1-4.9; [4], §§1.7-1.10; [5], п. 2.1; [6], гол. 5
ТЕОРЕТИЧНІ ВІДОМОСТІ
Знаходження наближених значень дійсних коренів нелінійного рівняння:
f(x)=0	(26)

виконують у два етапи:

відокремлюють корені, тобто визначають проміжки на числовій осі Ox, на кожному з яких знаходиться єдиний (відокремлений) корінь рівняння;

уточнюють відокремлені корені до потрібного наближення.

Метод послідовного перебору для відокремлення коренів базується на таких положеннях:

-якщо неперервна на відрізку [a; b] функція приймає на його кінцях значення різних знаків (тобто f(a) f(b)<0), то рівняння (26) має на цьому відрізку принаймні один корінь;

-якщо функція f(x) до того ж ще й строго монотонна, то корінь на відрізку [a; b] єдиний.

Рис.1

Рис.2

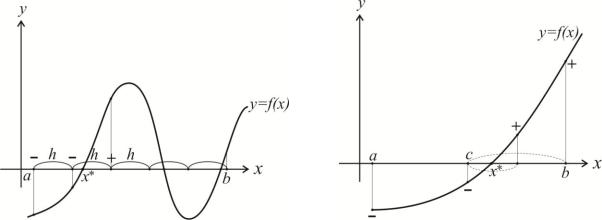
Виходячи з приблизного графіка функції f(x), визначають інтервал [a; b]. Далі обчислюють значення f(x), починаючи з точки x a , рухаючись управо з деяким кроком h (рис.1). Як тільки виявиться пара сусідніх значень f(x), яка має різні знаки, і функція f(x) монотонна на цьому відрізку, так відповідні значення аргументу x (попереднє й наступне) можна вважати кінцями відрізку, що містить корінь.

Основні методи розв’язання нелінійних рівнянь є ітераційними. В таких методах корінь рівняння x* визначається як границя послідовності x(0), x(1), …, x(k) і неможливо визначити наперед кількість необхідних кроків для отримання рішення.

В методі половинного ділення (рис. 2) інтервал відокремлення кореня [a; b]

ділять навпіл і в серединну точку c a b , переміщують той кінець інтервалу

(a чи b), в якому знак функції збігається зі знаком f ( c ). Процес ділення продовжують то тих пір, поки не виконається умова f (c) або b a , де - точність.

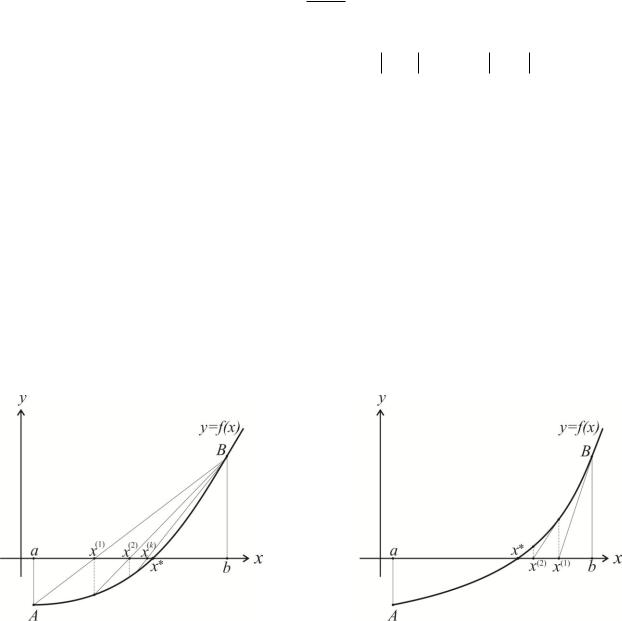
У методі січних ділення відрізку [a; b] відбувається пропорційно значенню функції в точках a та b (рис. 3). В цьому випадку точка поділу відрізка буде знаходитися на перетині хорди AB із віссю 0x, а її абсциса x(1) є першим наближеним значенням кореня. Щоб уточнити x(1), застосуємо метод хорд до відрізка [x(1), b] отримаємо друге наближення – x(2), і так далі. Нерухомим буде той кінець відрізка ізоляції кореня , в якому знак функції f(x) збігається зі знаком другої похідної.

Розрахункова формула методу січних:

x(k 1) x(k )	f (x(k ) )	(x(k ) ),		(27)
	f (x(k ) ) f ( )

де =a, x(0)=b, якщо f(a) f”(a)>0, або =b, x(0)=a, якщо f(b) f”(b)>0.
Розрахунки продовжують до виконання умови			x(k 1) x(k )	.

Рис.3

Рис.4

У методі Ньютона ділянка кривої y=f(x) послідовно замінюється її дотичною в точці A або B (рис.4). Абсциса точки перетину дотичної з віссю 0x – x(1)

буде першим наближеним значенням кореня. Щоб уточнити x(1) застосуємо метод дотичних до відрізка [a; x(1)], отримаємо друге наближення – x(2), і так далі. Точка, в якій будується дотична, обирається з умови співпадання знаків функції та її другої похідної f(x) f”(x)>0.

Розрахункова формула методу Ньютона:

x(k 1)	x(k )	f (x(k ) )			,	(28)
			(k )	)
		f (x

де x(0)=a, якщо f(a) f”(a)>0, або x(0)=b, якщо f(b) f”(b)>0.

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.07.2019375.23 Кб3Поперешняк, Звукові карти.rtf
#
17.09.2019153.09 Кб2Порядок виконання роботи.doc
#
12.08.2019732.67 Кб44Посібник з англійської мови.doc
#
15.11.20193.38 Mб19Посібник Ковтуненко.doc
#
22.11.20191.92 Mб15Посібник корозія.doc
#
23.02.20164.07 Mб19Посібник ЧМ.pdf
#
20.12.20183.68 Mб10Посібник. БЖД. Желібо..doc
#
23.02.2016169.98 Кб4Пояс Вода.doc
#
16.09.20192.91 Mб7Пояснювальна до курсової.docx
#
23.04.2019802.3 Кб10ПР № 12, 13.doc
#
23.04.2019307.71 Кб6Пр № 4.doc