Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Посібник ЧМ

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

4.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>


	i	0	1		2		3	4
14.	xi	0	1		2		3	4
14.	fi	1.27	0.23		1.29		0.78	0.24
	fi	1.27	0.23		1.29		0.78	0.24
	~	0.53		1.53		2.53		3.53
	xi	0.53		1.53		2.53		3.53

	i	0	1		2		3	4
15.	xi	-2	-1		0		1	2
15.	fi	0.25	1.03		0.79		0.26	0.36
	fi	0.25	1.03		0.79		0.26	0.36
	~	-1.8		-0.8		0.8		1.8
	xi	-1.8		-0.8		0.8		1.8

	i	0	1		2		3	4
16.	xi	0	1		2		3	4
16.	fi	1.31	0.26		1.73		0.76	0.27
	fi	1.31	0.26		1.73		0.76	0.27
	~	0.25		1.25		2.25		3.25
	xi	0.25		1.25		2.25		3.25

	i	0	1		2		3	4
17.	xi	0	1		2		3	4
17.	fi	1.36	0.28		1.42		0.74	0.28
	fi	1.36	0.28		1.42		0.74	0.28
	~	0.85		1.85		2.85		3.85
	xi	0.85		1.85		2.85		3.85

	i	0	1		2		3	4
18.	xi	-2	-1		0		1	2
18.	fi	1.35	0.29		1.45		0.74	0.34
	fi	1.35	0.29		1.45		0.74	0.34
	~	-1.47		-0.47		0.47		1.47
	xi	-1.47		-0.47		0.47		1.47

	i	0	1		2		3	4
19.	xi	-2	-1		0		1	2
19.	fi	1.37	0.31		1.52		0.75	0.33
	fi	1.37	0.31		1.52		0.75	0.33
	~	-1.51		-0.51		0.51		1.51
	xi	-1.51		-0.51		0.51		1.51

	i	0	1		2		3	4
20.	xi	0	1		2		3	4
20.	fi	1.44	0.33		1.55		0.66	0.77
	fi	1.44	0.33		1.55		0.66	0.77
	~	0.56		1.56		2.56		3.56
	xi	0.56		1.56		2.56		3.56

	i	0	1		2		3	4
21.	xi	0	1		2		3	4
21.	fi	0.0	0.72		1.56		2.84	7.73
	fi	0.0	0.72		1.56		2.84	7.73
	~	0.35		1.35		2.35		3.35
	xi	0.35		1.35		2.35		3.35


	i	0	1		2		3	4
22.	xi	1	2		3		4	5
22.	fi	2.8	1.82		1.61		1.57	1.56
	fi	2.8	1.82		1.61		1.57	1.56
	~	1.66		2.66		3.66		4.66
	xi	1.66		2.66		3.66		4.66

	i	0	1		2		3	4
23.	xi	-2	-1		0		1	2
23.	fi	-2.22	-0.19		0.79		1.56	2.23
	fi	-2.22	-0.19		0.79		1.56	2.23
	~	-1.85		-0.85		0.85		1.85
	xi	-1.85		-0.85		0.85		1.85

	i	0	1		2		3	4
24.	xi	-2	-1		0		1	2
24.	fi	-1.86	-0.63		1.0		3.72	9.39
	fi	-1.86	-0.63		1.0		3.72	9.39
	~	0.25		1.25		2.25		3.25
	xi	0.25		1.25		2.25		3.25

	i	0	1		2		3	4
25.	xi	0	1		2		3	4
25.	fi	0.0	3.05		5.24		7.35	9.47
	fi	0.0	3.05		5.24		7.35	9.47
	~	0.83		1.83		2.83		3.83
	xi	0.83		1.83		2.83		3.83

	i	0	1		2		3	4
26.	xi	-1	0		1		2	3
26.	fi	0.43	0.24		0.03		0.12	1.42
	fi	0.43	0.24		0.03		0.12	1.42
	~	-0.4		0.4		1.4		2.4
	xi	-0.4		0.4		1.4		2.4

	i	0	1		2		3	4
27.	xi	-2	-1		0		1	2
27.	fi	-0.27	-0.37		0.0		2.71	4.77
	fi	-0.27	-0.37		0.0		2.71	4.77
	~	-1.25		-0.25		0.25		1.25
	xi	-1.25		-0.25		0.25		1.25

	i	0	1		2		3	4
28.	xi	0	1		2		3	4
28.	fi	0.0	0.45		0.52		0.0	-2.26
	fi	0.0	0.45		0.52		0.0	-2.26
	~	0.38		1.38		2.38		3.38
	xi	0.38		1.38		2.38		3.38

	i	0	1		2		3	4
29.	xi	0	1		2		3	4
29.	fi	0.0	0.26		0.96		1.57	1.30
	fi	0.0	0.26		0.96		1.57	1.30
	~	0.47		1.47		2.47		3.47
	xi	0.47		1.47		2.47		3.47


	i	0	1		2		3	4
30.	xi	2	3		4		5	6
30.	fi	10.0	2.0		1.11		0.77	0.59
	fi	10.0	2.0		1.11		0.77	0.59
	~	2.34		3.34		4.34		5.34
	xi	2.34		3.34		4.34		5.34

ПРИКЛАД РОЗРАХУНКІВ

1. Побудувати кубічний сплайн для функції, що задана таблицею, і знайти його зна-

чення у вказаних точках ~ . x


i	0	1		2	3	4
xi	-2	-1		0	1	2
fi	1.36	0.75		-1.21	0.33	-0.25
~	-1.3		-0.3		0.3	1.3
xi	-1.3		-0.3		0.3	1.3

Побудуємо чотири сплайн-функції для кожного з інтервалів:

[ 2; 1]	− S		0	(x) a		0	b (x x			0	) c		0	(x x			0	)2	d			0	(x x	0	)3 ,
			0			0		0		0			0				0					0		0
[ 1; 0]	− S1(x) a1 b1(x x1) c1(x x1)2 d1(x x1)3 ,
[0;1]	−	S2 (x) a2					b2 (x x2 ) c2 (x x2 )2 d2 (x x2 )3 ,
[1; 2]	−	S	3	(x) a			b (x x ) c (x x )2 d													3	(x x )3 .
			3		3			3	3			3				3				3			3
Знаходимо коефіцієнти сплайн-функцій. Уведемо початкові дані: значення інтерполяцій-
них вузлів - , значення функції у вузлах -								, значення точок, у яких інтерполюється функція - .
					2				1.36								1.3
					1				0.75								1.3
					1				0.75								0.3
		x			0			f	1.21					z			0.3
		x			0			f	1.21					z			0.3
																	0.3
					1				0.33
																	1.3
					2				0.25
Знаходимо коефіцієнти ai i 0,..., n 1:
																1.36
				i 0			3	ai fi				a				0.75
				i 0			3	ai fi				a			1.21
															1.21

																0.33

Для знаходження коефіцієнтів сi i 0,..., n потрібно скласти систему лінійних алгебраїчних рівнянь, яку розв’яжемо за допомогою спеціального обчислювального блоку Mathcad Given/Find:

				4	1	0
i 0 4	ci 0	F		1	4	1	i 0 2	gi 3 fi 2 2 fi 1 fi

				0	1	4		0
								0
	c1							1.948

Given	F c2		g	c Find(c)			c	3.744


								2.526
	c3							2.526

								0
						73

Знаходимо коефіцієнти di , bi i 0,..., n 1, де h – крок між вузлами інтерполяції:

h 1

0.649

ci 1 ci

1.897

i 0 2

3 h

2.09

0.842

0.039

fi 1

i 0 3

ci 1 2 ci

1.909

0.114

1.104

Тепер можемо записати сплайн-функції для кожного інтервалу:

[ 2; 1]	−	S	0	(x) 1.36 0.039(x 2) 0.649(x 2)3 ,
			0
[ 1; 0]	−	S1(x) 0.75 1.909(x 1) 1.948(x 1)2			1.897(x 1)3 ,
					(*)
[0;1]	−	S2 (x) 1.21 0.114x 3.744x2 2.09x3 ,
[1; 2]	−	S	3	(x) 0.33 1.104(x 1) 2.526(x 1)2	0.842(x 1)3 .
			3

Використовуючи отримані сплайни знайдемо значення функції f(x) у заданих точках:

			1.165
i 0 3	Si ai bi zi xi ci zi xi 2 di zi xi 3	S	0.89
			0.964

			0.457

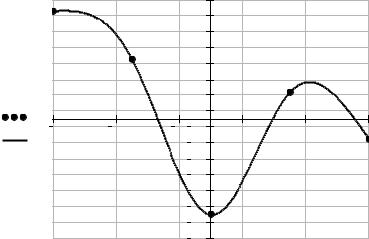
Знайдемо розв’язок цієї ж задачі, використовуючи функції середовища Mathcad.

v lspline(x f)		y(t) interp(v x f t)
			1.5
			1.3
			1.1
			0.9
			0.7
			0.5
			0.3
f			0.1
			0.1
y( t)	2	1.2	0.4 0.1	0.4	1.2	2
			0.3
			0.5
			0.7
			0.9
			1.1
			1.3
			1.5

x t

Тут функція interp(v,x,f,t) апроксимує дані векторів x і f кубічними сплайнами. v – вектор других похідних, створений функцією lspline(x,f), яка спирається на умову (54). Із графіку видно, що побудований сплайн y(t) у вузлах інтерполяції приймає задані значення y(ti ) f (xi ), ti xi , i 0,1,..., n .

Порівняємо графіки і значення отриманих сплайн-функції (*) з функцією y(t) на кожному інтервалі.

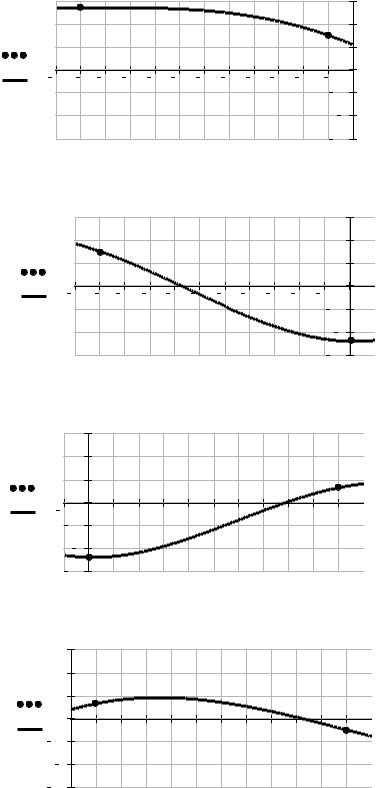
i 0 3

S(i t) ai bi t xi ci t xi 2 di t xi 3

інтервал [ 2; 1] :

											1.5
											1
f											0.5
											0.5
y( t)
2.1	2	1.9	1.8	1.7	1.6	1.5	1.4	1.3	1.2	1.1	1
S(0 t)											0.5
											1
											1.5
						x t
інтервал [ 1; 0] :
											1.5
											1
f											0.5
											0.5
y( t)
	1.1	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0
S(1 t)											0.5
											1
											1.5
							x t

y( 1.3) 1.165

S(0 1.3) 1.165

y( 0.3) 0.89 S(1 0.3) 0.89

інтервал [0;1] : 1.5

1.51

f		10.5
		10.5
y( t)
f	00..51		0 0.1	0.2 0.3		0.4	0.5 0.6		0.7	0.8	0.9	1
	00..51		0 0.1	0.2 0.3		0.4	0.5 0.6		0.7	0.8	0.9	1	y(0.3)	0.964
S(2 t)		0.5											y(0.3)	0.964
y( t)
	0.1	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
S(2 t)		1											S(2 0.3) 0.964
	0.5												S(2 0.3) 0.964
	0.5
		11.5
	1.5						x t
	1.5

x t

інтервал [1; 2]:

	1.5
	1
f	0.5
	0.5											y(1.3) 0.457
y( t)												y(1.3) 0.457
y( t)
	0.9	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2	0.457
S(3 t) 0.5												S(3 1.3)	0.457
S(3 t) 0.5

1.5

x t

Як бачимо, побудовані сплайн-функції (*) мають повне співпадання з функцією y(t). Отже, задача розв’язана коректно.

КОНТРОЛЬНІ ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

1.Коли використовується інтерполяція функцій?

2.Що таке сплайн-інтерполяція?

3.Що таке кубічний сплайн і як його побудувати?

4.Переваги і недоліки інтерполяції сплайнами.

5.З якими ще методами наближення функцій Ви знайомі?

ТЕМА 8. Чисельне диференціювання

Лiтература: [2], пп. 1.1-1.3; [4], §§2.8-2.11; [5], п. 3.3; [6], гол. 8

ТЕОРЕТИЧНІ ВІДОМОСТІ

Формули чисельного диференціювання, як правило, використовуються, якщо функція від якої треба знайти похідну задана табличним способом. При розв’язанні практичних задач використовують наближення перших та других похідних.

Найпростішими формулами чисельного диференціювання замінюють зна-

чення похідної в	точці. Нехай функція f (x)	задана в точках xi 1, xi , xi 1
(xi 1 xi xi xi 1	h) значеннями yi 1, yi , yi 1 .	Тоді значення похідної в точці

xi можна визначити за формулами:

f (xi )

yi 1 yi

– права різницева похідна;

(56)

f (xi )

yi yi 1

– ліва різницева похідна;

(57)

f (xi )

yi 1 yi 1

– центральна різницева похідна.

(58)

Похибки

формул

(56), (57) мають перший порядок

точності

по h

пр

max

f '' ( )

max

f '' ( )

, а формула

(58) –

другий

[ xi ; xi 1 ]

[ xi 1 ; xi ]

max

f ''' ( )

[ xi 1 ; xi 1 ]

Значення другої похідної обчислюють відповідно за формулою:

yi 1 2 yi yi 1

(59)

(xi )

яка має другий порядок точності

max

f IV ( )

[ xi 1 ; xi 1 ]

Більш точні формули можна отримати при використанні інтерполяційних

поліномів.

Нехай функція

f (x)

задана таблично на відрізку [a;b] в точках

a, x

x i h,

b a

n N значеннями f (x

) y ,

i 0, n , де

f (x1) y1, ..., f (xn ) yn . Щоб отримати формули наближеного диференціювання, замінюють функцію інтерполюючою функцією F (x) , а потім вважають:

f (x) F (x) на x [a;b].

Аналогічно чинять при знаходженні похідної другого порядку.

Але слід зауважити, що наближене диференціювання являє собою операцію менш точну, ніж інтерполювання. Дійсно близькість ординат двох кривих

y f (x) та y F (x) на відрізку [a;b] , ще не гарантує близькості на цьому відрізку їхніх похідних f (x) та F (x).

Формули першої та другої похідної у випадку нерівновіддалених вузлів

отримають диференціюванням інтерполяційного полінома Ньютона:

Pn (x) f (x0 ) (x x0 ) f (x0 ; x1) (x x0 )(x x1) f (x0 ; x1; x2 )

(x x0 )(x x1) (x x2 ) f (x0 ; x1; x2 ; x3 )

(x x0 )(x x1) (x x2 ) (x x3 ) f (x0 ; x1; x2 ; x3; x4 ) ...

f (x0 ) (x x0 ) f (x0 ; x1) (x2 x(x0 x1) x0 x1) f (x0 ; x1; x2 )

(x3 x2 (x0 x1 x2 ) x(x0 x1 x0 x2 x1x2 ) x0 x1x2 ) f (x0 ; x1; x2 ; x3 )

(x4 x3 (x0 x1 x2 x3 ) x2 (x0 x1 x0 x2 x0 x3 x1x2 x1x3 x2 x3 )

x(x0 x1x2 x0 x1x3 x0 x2 x3 x1x2 x3 ) x0 x1x2 x3 ) f (x0 ; x1; x2 ; x3; x4 ) ... .

Тут f (x0; x1), f (x0; x1; x2 ) ,						f (x0; x1; x2 , x3 ) , f (x0; x1; x2 , x3, x4 )															- поділені різниці.
Pn (x) f (x0 ; x1) (2x x0 x1) f (x0 ; x1; x2 )
(3x2 2x(x x x					2	) x x x x			2	x x			2	) f (x ; x ; x					2	; x )
	0	1			2	0	1	0	2			1	2		0	1			2	3			(60)
(4x3 3x2 (x x x																							(60)
(4x3 3x2 (x x x			2	x ) 2x(x x x x							2	x x x x					2	x x x				2	x )
0	1		2		3		0	1		0	2			0	3	1	2			1	3	2	3
(x0 x1x2 x0 x1x3 x0 x2 x3 x1x2 x3 )) f (x0 ; x1; x2 ; x3; x4 ) ... .

Pn (x) 2 f (x0 ; x1; x2 ) (6x 2(x0 x1 x2 )) f (x0 ; x1; x2 ; x3 )

(12x2 6x(x0 x1 x2 x3 )

2(x0 x1 x0 x2 x0 x3 x1x2 x1x3 x2 x3 )) f (x0 ; x1; x2 ; x3; x4 ) ... .

Формули першої та другої похідної у випадку рівновіддалених вузлів можна

отримати диференціюванням інтерполяційного полінома Лагранжа:

q(q 1)

... (q n)

Ln (x) ( 1)n i yi

i 0

i!(n i)!(q i)

dLn (x)

dq 1

dLn (x)

1 n

( 1)n i

d q(q 1) ... (q n)

f x

(q i)

h i 0

i!(n i)! dq

Аналогічно визначають другу похідну:

( 1)

n i

q(q 1) ... (q n)

f x

i!(n i)!

(q i)

i 0

Формули (60), (61) мають n-ий порядок точності по h.

(61)

(62)

ЗАВДАННЯ

1.Обчислити першу та другу похідні від заданої функції f (x) в точці x2 , використовуючи найпростіші формули чисельного диференціювання. Оцінити похибку обчислень.

2.Обчислити першу та другу похідні від заданої функції f (x) в точці x2 , використовуючи інтерполяційні поліноми. Оцінити похибку обчислень.

1.		ex		x
	f (x) 2		e

2.	f (x)	e x2 x2
			2

3.f (x) sin(x) 1 e sin( x)

4.f (x) cos(x) 1 e cos(x)

5.				1

	f (x) x e x
6.		x2
6.	f (x) 1 x
	f (x) 1 x
7.	f (x) tg(x) x
8.	f (x)			x

		ln(x) 1
		ln(x) 1
				x	3
9.	f (x) tg			x
9.	f (x) tg
				3

10.	f (x)	3		x3 1

		2		x2 1
		2		x2 1
11.	f (x)	2	x	3		5
		7
						7 x
						7 x
12.	f (x) e 1x (ex 1)
13.	f (x) ln( 1 ee x )
14.	f (x)	sin(x) x cos(x)
14.	f (x)
						x

15.f (x) x ln(ln(x))

16.f (x) x sin(x) x2 cos(x) x

i	0	1	2	3	4
xi	1.0	1.25	1.5	1.75	2.0

i	0	1	2	3	4
xi	0.5	0.6	0.7	0.8	0.9

i	0	1	2	3	4
xi	0.6	0.7	0.8	0.9	1.0

i	0	1	2	3	4
xi	2.6	2.7	2.8	2.9	2.0

i	0	1	2	3	4
xi	0.3	0.4	0.5	0.6	0.7

i	0	1	2	3	4
xi	0.1	0.2	0.3	0.4	0.5

i	0	1	2	3	4
xi	0.3	0.4	0.5	0.6	0.7

i	0	1	2	3	4
xi	0.1	0.2	0.3	0.4	0.5

i	0	1	2	3	4
xi	0.2	0.3	0.4	0.5	0.6

i	0	1	2	3	4
xi	0.15	0.20	0.25	0.30	0.35

i	0	1	2	3	4
xi	0.15	0.20	0.25	0.30	0.35

i	0	1	2	3	4
xi	0.36	0.38	0.40	0.42	0.44

i	0	1	2	3	4
xi	0.2	0.3	0.4	0.5	0.6

i	0	1	2	3	4
xi	0.2	0.3	0.4	0.5	0.6

i	0	1	2	3	4
xi	1.20	1.25	1.30	1.35	1.40

i	0	1	2	3	4
xi	1.20	1.25	1.30	1.35	1.40

17.	f (x)	1	x	2		1	2
		3			3
							3 x2 1


18.	f (x)	0,25 x4					1
18.	f (x)				x
					x

19.f (x) ln(x x2 1)

			x2 1
20.	f (x)	2	x

			x2 2
			x2 2
21.	f (x)	x ln(x)
21.	f (x)	ln(x) 1
		ln(x) 1
22.	f (x)		1

		ln(x) 1 x
		ln(x) 1 x
23.	f (x)		1

		2(ln(x) 1) x
		2(ln(x) 1) x

24.f (x) e x 2 e x2 e x2

25.f (x) esin( x) e sin( x)

26.f (x) 1 1 e 2

x 

27. f (x) cos(sin( x)) sin(cos( x))

28.	f (x)		cos(2x) sin(2x)
28.	f (x)
					cos(x)
29.	f (x)			1			sin(x)		x

		cos(x)						cos(x)
		cos(x)						cos(x)
30.	f (x)		e2x			(3x 1)e x
30.	f (x)		3e	2			3e
			3e	2			3e

i	0	1	2	3	4
xi	1.2	1.3	1.4	1.5	1.6

i	0	1	2	3	4
xi	1.2	1.4	1.6	1.8	2.0

i	0	1	2	3	4
xi	1.4	1.45	1.5	1.55	1.6

i	0	1	2	3	4
xi	1.3	1.4	1.5	1.6	1.7

i	0	1	2	3	4
xi	1.0	1.25	1.5	1.75	2.0

i	0	1	2	3	4
xi	1.0	1.25	1.5	1.75	2.0

i	0	1	2	3	4
xi	2.0	2.25	2.5	2.75	3.0

i	0	1	2	3	4
xi	1.2	1.3	1.4	1.5	1.6

i	0	1	2	3	4
xi	1.2	1.3	1.4	1.5	1.6

i	0	1	2	3	4
xi	1.4	1.45	1.5	1.55	1.6

i	0	1	2	3	4
xi	0.2	0.3	0.4	0.5	0.6

i	0	1	2	3	4
xi	0.6	0.65	0.7	0.75	0.8

i	0	1	2	3	4
xi	0.2	0.3	0.4	0.5	0.6

i	0	1	2	3	4
xi	2.2	2.3	2.4	2.5	2.6

ПРИКЛАД РОЗРАХУНКІВ

1.Обчислити першу та другу похідні від заданої функції f(x) в точці x2 , використовую-

чи найпростіші формули чисельного диференціювання. Оцінити похибку обчислень.

	e x
f (x)	e x		i	0	1	2	3	4
		,
	x	,	xi	1.0	1.25	1.5	1.75	2.0

Отримаємо значення функції в заданих точках:

f (x) ex x

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.07.2019375.23 Кб3Поперешняк, Звукові карти.rtf
#
17.09.2019153.09 Кб2Порядок виконання роботи.doc
#
12.08.2019732.67 Кб44Посібник з англійської мови.doc
#
15.11.20193.38 Mб19Посібник Ковтуненко.doc
#
22.11.20191.92 Mб15Посібник корозія.doc
#
23.02.20164.07 Mб19Посібник ЧМ.pdf
#
20.12.20183.68 Mб10Посібник. БЖД. Желібо..doc
#
23.02.2016169.98 Кб4Пояс Вода.doc
#
16.09.20192.91 Mб7Пояснювальна до курсової.docx
#
23.04.2019802.3 Кб10ПР № 12, 13.doc
#
23.04.2019307.71 Кб6Пр № 4.doc