1.8. Приклади розв’язування індивідуальних задач

Задача 1.1.

1. Задане в алгебраїчній формі число записати в тригонометричній та показниковій формах.

Розв’язування.

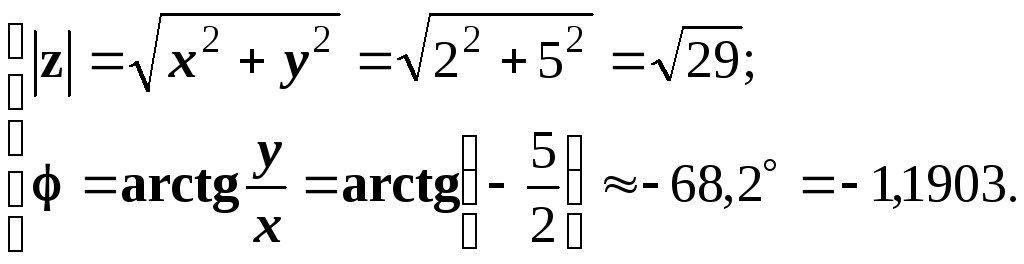
_{В тригонометричній формі:}

В показниковій формі: .

2. Задане в алгебраїчній формі число записати в тригонометричній та показниковій формах.

Розв’язування.

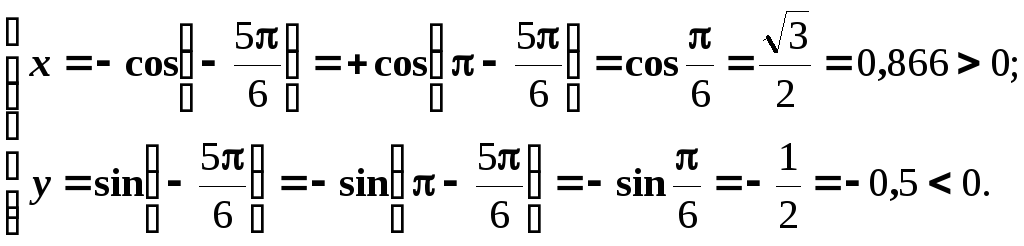
_{В тригонометричній формі:}

В показниковій формі:

Задача 1.2. Спростити вираз до числа в алгебраїчній формі.

Розв’язування.

1. ;.

.

.

2. .

.

.

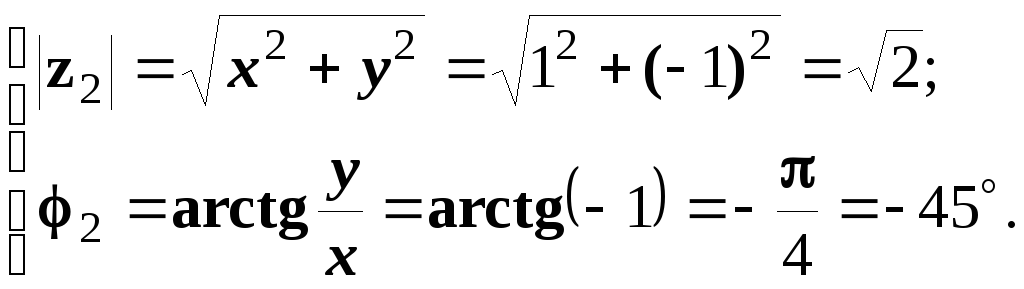
3. .

.

.

Задача 1.3. Знайти корені .

Розв’язування. Так як n = 3, то одержимо три корені.

; ,k = 0, 1, 2.

1.

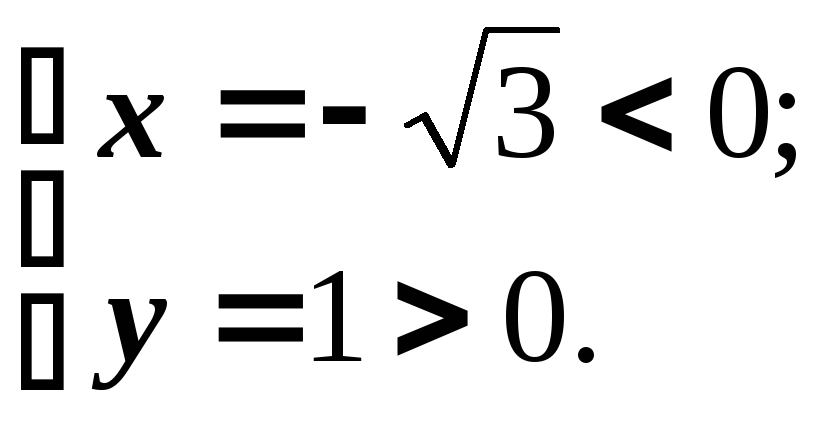
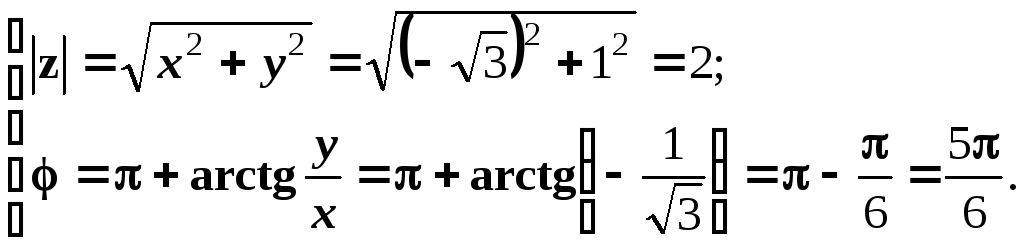
Отже,

.

2. .

3. .

4. ,k = 0, 1, 2.

.

. Отже, .

. Отже, .

Значення зменшуємо на. Тоді

. Отже, .

5. .

Отже,

6. ;

;

.

Зобразимо всі три корні на колі радіуса.

1.9. Контрольні запитання

1. Уявна одиниця та її властивість.

2. Алгебраїчна форма комплексного числа, його модуль, реальна та уявна частини.

3. Додавання та множення комплексного чисел в алгебраїчній формі.

4. Віднімання та ділення комплексних чисел в алгебраїчній формі.

5. Геометрична форма комплексного числа, полярні координати.

6. Перехід від декартових координат до полярних.

7. Аргумент числа z та його головне значення.

8. Формула визначення через значення .

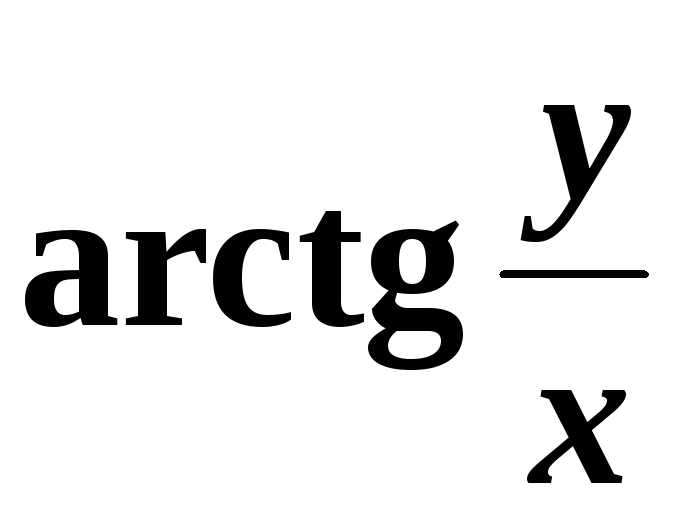9. Додавання та віднімання векторів, що зображують комплексне число.

10. Тригонометрична форма комплексного числа та її особливості.

11. Множення та ділення комплексних чисел в тригонометричній формі.

12. Формула Муавра.

13. Добування кореня степеня n, основні формули.

14. Алгоритм добування кореня степеня n.

15. Яке число коренів має вираз ?

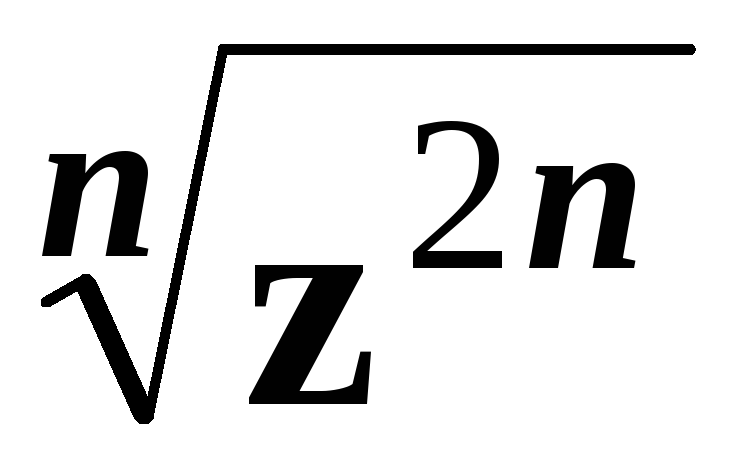16. Формула Ейлера.

17. Показникова форма комплексного числа.

18. Множення та ділення комплексних чисел в показниковій формі.

19. Спряжені комплексні числа, їх модулі, сума та добуток.

20. Довести, що .

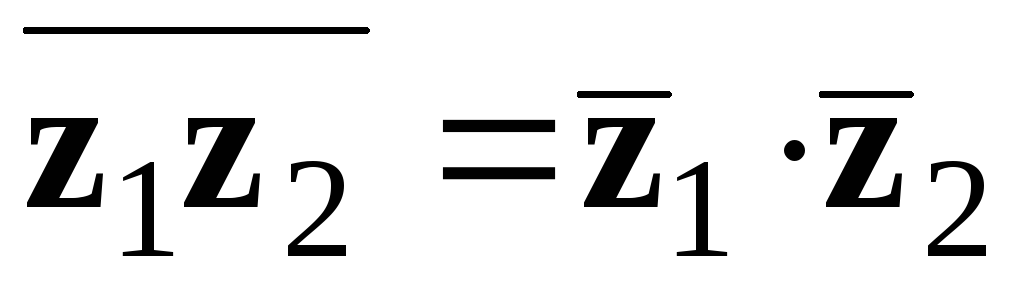21. Які дії над комплексними числами зручно здійснювати, якщо вони задані в алгебраїчній, тригонометричній та показниковій степенях.

22. Що одержують при діленні та множенні числа z на уявну одиницю i.

23. Скільки значень має вираз 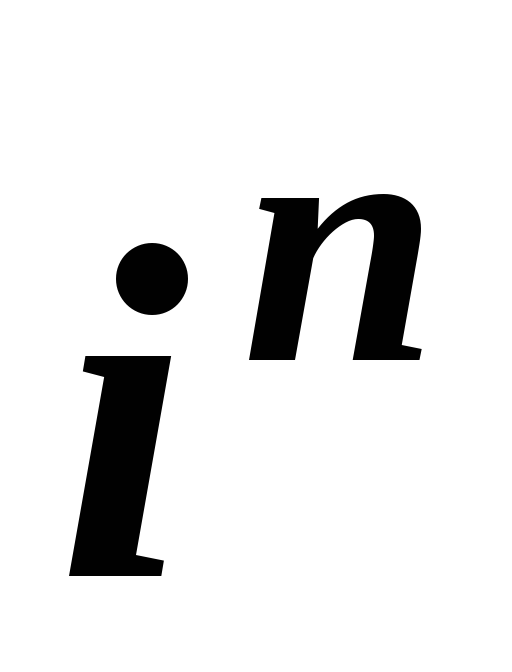для цілих дійсних n та n = 0.

24. Формула та характерні точки одиничного кола на комплексній площині.

33