
- •Практикум 1 Комплексні числа та дії над ними
- •1.1. Теоретичні та довідкові дані
- •1.2. Алгебраїчна форма комплексного числа
- •1.3. Геометрична форма комплексного числа
- •1.4. Тригонометрична форма комплексного числа
- •1.4.1. Множення та ділення комплексних чисел
- •1.5. Показникова форма комплексного числа
- •1.5.1. Спряжені комплексі числа
- •Висновки
- •1.6. Приклади
- •1.7. Індивідуальні завдання
- •1.8. Приклади розв’язування індивідуальних задач
- •1.9. Контрольні запитання
1.5.1. Спряжені комплексі числа
Особливу роль в розробці теорії та методів цифрової обробки сигналів відіграють спряжені комплексні числа.
Комплексне
число
![]() називають комплексно спряженим до
комплексного числа
називають комплексно спряженим до
комплексного числа![]() .
Ця пара чисел є взаємно комплексно
спряженими, бо
.
Ця пара чисел є взаємно комплексно
спряженими, бо![]() .
.
При алгебраїчній формі комплексно спряжені числа відрізняються знаком уявної частини.
Основні властивості комплексно спряжених чисел:
![]() ,
(1.52)
,
(1.52)
![]() ,
(1.53)
,
(1.53)
![]() ,
(1.54)
,
(1.54)
![]() ,
,
![]() .
(1.55)
.
(1.55)
Спряжені комплексні числа зображуються такими точками, що розташовані симетрично відносно дійсної осі х (рис. 1.9).

Рис. 1.9. Векторне зображення основних властивостей комплексно-спряжених чисел
Тому, згідно рис. 1.9:
![]() .
(1.55)
.
(1.55)
![]() .
(1.56)
.
(1.56)
![]() .
(1.57)
.
(1.57)
Також корисними є формули:
![]() .
(1.58)
.
(1.58)
![]() .
(1.59)
.
(1.59)
![]() ,
(1.60)
,
(1.60)
бо,
якщо z = x + yi,
то
![]() ,
а
,
а
![]() .
.
П
Рис
1.9.![]() :
:
![]() .
(1.61)
.
(1.61)
При показниковій формі комплексного числа:
![]()
 .
(1.62)
.
(1.62)
Отже,
при переході до комплексного спряженого
числа
![]() в числіz,
що задано в тригонометричній або
показниковій формах, можна поміняти
знак аргументу
на протилежний.
в числіz,
що задано в тригонометричній або
показниковій формах, можна поміняти
знак аргументу
на протилежний.
Важливою для нас є формула:
![]() .
(1.63)
.
(1.63)
Дійсно, з одного боку (рис. 1.10):
![]() ,
,
![]() .
.
З іншого боку
![]() .
.
Тому,
![]() ,
що відповідає формулі (1.63).
,
що відповідає формулі (1.63).
Висновки
Застосування комплексних чисел в цифровій обробці сигналів потребує різних форм запису комплексних чисел. Вказані раніше особливості комплексних чисел залежно від форми запису зведено в таблицю 1.1.
Таблиця 1.1.
Параметри комплексних чисел в залежності від форми запису
|
Форма параметр |
Алгебраїчна |
Тригонометрична |
Показникова |
|
z |
x + yi |
|
|
|
|
|
r |
|
|
Arg z |
|
|
|
|
|
x yi |
|
|
|
Зручно здійснювати |
Додавання та віднімання |
Множення та ділення |
Множення, ділення, диференціювання, інтегрування |
1.6. Приклади
Приклад
1.1.
Визначити
число
![]() ,
де n
–
ціле дійсне число або нуль.
,
де n
–
ціле дійсне число або нуль.
Розв’язування. Спочатку розглянемо додатні значення n. Будемо послідовно множити число і на число і:
n = 1:
![]() ;
;
n = 2:
![]() (по визначенню);
(по визначенню);
n = 3:
![]() ;
;
n = 3:
![]()
і так далі.
Результати послідовного множення на число і показані на рис. 1.11, а.
При
множенні числа
![]() на
уявну одиницю і
число z
треба
повернути на кут
на
уявну одиницю і
число z
треба
повернути на кут ![]() по одиничному колу за годинниковою
стрілкою.
по одиничному колу за годинниковою
стрілкою.

Рис. 1.11.
Функція
Рис.1.11.![]()
![]() ,
то загальна формула для визначення
числа
,
то загальна формула для визначення
числа
![]() при
n ≥ 0
набуває вигляду:
при
n ≥ 0
набуває вигляду:
 (1.64)
(1.64)
де k = 0, 1, 2, ….
При
збільшенні степеня на 4 число
![]() повторює
своє значення. Тому, будь-яке число n
ділимо на 4, тоді ціла частина від
ділення є число k.
Наприклад:
повторює
своє значення. Тому, будь-яке число n
ділимо на 4, тоді ціла частина від
ділення є число k.
Наприклад:
![]() .
.
При
n < 0
процедура аналогічна
(рис. 1.11, b).
Так як множення на , тобто рівносильне
діленню на і,
то число z
треба повернути на кут ![]() за
годинниковою стрілкою. Загальна формула
числа
за
годинниковою стрілкою. Загальна формула
числа
![]() при
n < 0
має вигляд:
при
n < 0
має вигляд:
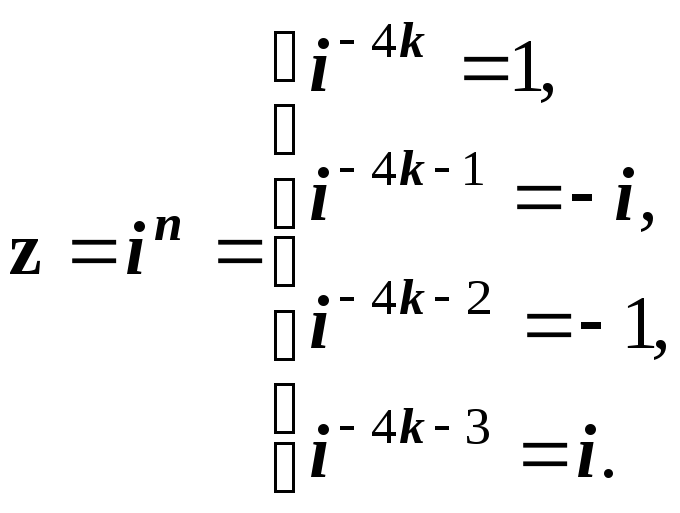 (1.65)
(1.65)
Наприклад:
.
Порівнюючи
формули (1.64)
та (1.65)
та користуючись рис. 1.11, а
та рис. 1.11, b,
бачимо, що для парних n:
![]() ,
а для непарних n:
–
,
а для непарних n:
–
![]() .
.
Приклад
1.2. Спростити
вираз
![]() .
.
Розв’язування. Дії множення та піднесення до степеня комплексних чисел, що задані в алгебраїчній формі, будемо виконувати за правилами множення алгебраїчних многочленів. Спочатку кожний множник піднесемо до степеня і спростимо, а потім результати перемножимо.
![]()
![]() .
.
Зауважимо, що будь-який проміжний результат є комплексним числом, а отже, зводиться до двочлена. Тому алгебра многочленів комплексних чисел зводиться до алгебри двочленів.
Приклад
1.3. Записати
вираз
![]() в
алгебраїчній формі.
в
алгебраїчній формі.
Розв’язування. Помноживши чисельник та знаменник на i, одержимо:
![]() .
.
Приклад 1.4. Записати
число
![]() в
алгебраїчній формі.
в
алгебраїчній формі.
Розв’язування. Помножимо
чисельник та знаменник на число
![]() ,
яке є спряженим до числа
,
яке є спряженим до числа![]() ,
що стоїть в знаменнику, а потім
скористаємося формулою (1.54):
,
що стоїть в знаменнику, а потім
скористаємося формулою (1.54):
![]() .
.
Реальна
частина:
![]() ,
уявна частина:
,
уявна частина:![]() .
.
Приклад 1.5. Записати
число
![]() в
тригонометричній формі.
в
тригонометричній формі.
Розв’язування. Тригонометрична форма комплексного числа має вигляд
,
де модуль числа z згідно (1.6) дорівнює
![]() .
.
Так
як
![]() ,
а
,
а![]() ,
то головне значення аргументу згідно
формули (1.17) дорівнює:
,
то головне значення аргументу згідно
формули (1.17) дорівнює:
![]()
![]() .
.
Отже,
![]() .
.
Приклад 1.6. Записати
число
![]() в
тригонометричній формі.
в
тригонометричній формі.
Розв’язування. Спочатку числу z надамо алгебраїчної форми:
![]()
![]()
![]() .
.
Модуль числа z дорівнює:
![]() .
.
Так
як
![]() ,
а
,
а![]() ,то
згідно (1.17):
,то
згідно (1.17):
![]() .
.
Таким
чином,
![]() .
.
Приклад
1.7. Записати
число
![]() в
алгебраїчній формі.
в
алгебраїчній формі.
Розв’язування. Спочатку
число
![]() запишемо в тригонометричній формі, а
потім скористаємося формулою Муавра.
запишемо в тригонометричній формі, а
потім скористаємося формулою Муавра.
![]() .
.
Так
як
![]() ,то
згідно (1.17):
,то
згідно (1.17):
![]() .
.
Отже,
![]() .
.
Згідно формулам (1.29) та (1.30)
![]()
![]()
![]() .
.
Було
відкинуто ціле число повних обертів
кута
![]() .
Так як –26 = 13(–2π),
то було відкинуто 13 обертів за годинниковою
стрілкою.
.
Так як –26 = 13(–2π),
то було відкинуто 13 обертів за годинниковою
стрілкою.
Приклад
1.8.
Знайти
всі значення кореня
![]() .
.
Розв’язування.
 .
.
Отже,
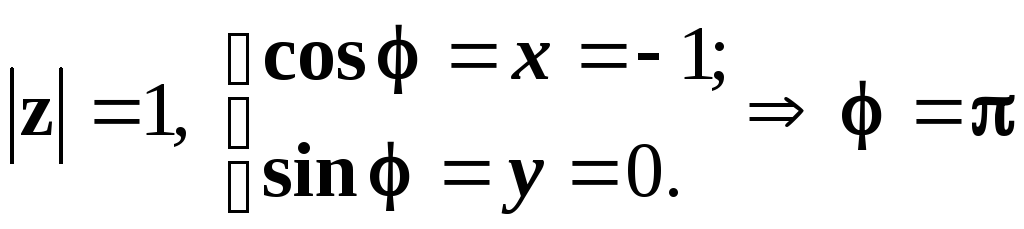 .
.
Таким чином, тригонометрична форма числа z набуває вигляду:
![]() .
.
Згідно формулам (1.33), (1.34) та (1.35)
![]() ,
k = 0, 1, 2.
,
k = 0, 1, 2.
n = 3,
![]() .
.
При відповідних значеннях k корені дорівнюють:
![]() ,
при k = 0;
,
при k = 0;
![]() ,
при k = 1;
,
при k = 1;
![]()
![]() ,
при k = 2.
,
при k = 2.
Всі три корені зображені на рис.1.12.
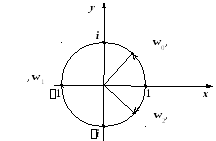
Рис. 1.12.
Приклад
1.9. Записати
в показниковій формі комплексне число
![]() .
.
Розв’язування. Згідно формули (1.43)
![]() .
.
Знайдемо
модуль
![]() та головне значення аргументу = arg z
числа
z.
та головне значення аргументу = arg z
числа
z.
![]() .
.
Так
як
![]() ,то
згідно (1.17):
,то
згідно (1.17):
![]() .
.
Отже,
![]() .
.
Приклад
1.10. Розділити
число
![]() на
число .
на
число .
Розв’язування. Запишемо
число
![]() в
показниковій формі. Так як
(див. приклад 1.7), то
в
показниковій формі. Так як
(див. приклад 1.7), то
![]() .
.
Згідно формули (1.47):
![]() .
.
