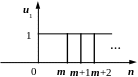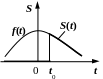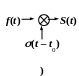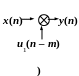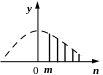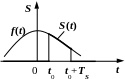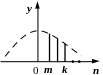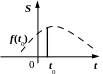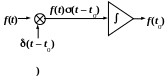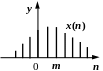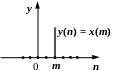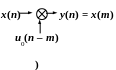ПРАКТИКУМ 2

Сигнал та його основні характеристики

2.1. Теоретичні та довідкові дані

2.1.1. Математична модель сигналу

Сигнал – фізичний процес, з допомогою якого в просторі та в часі відбувається перенесення інформації про досліджуваний об’єкт чи фізичне явище.

Найсуттєвіші властивості сигналів вивчають, абстрагуючись від їх фізичної природи. Для того, щоб сигнал став об’єктом теоретичного вивчення, необхідно вибрати метод його математичного описання, тобто створити математичну модель сигналу.

Виділимо п’ять основних етапів здійснення математичного моделювання сигналів:

• Вивчення фізичної природи сигналів та пошук відповідних математичних форм їх запису.

• Оцінка адекватності моделі, тобто встановлення прийнятої відповідності математичної моделі та фізичного явища. Така оцінка здійснюється шляхом порівняння їх відповідних параметрів, характеристик, закономірностей, тощо. Математична модель повинна відображати найсуттєвіші властивості сигналу і при цьому буди водночас якомога точнішою і простішою. Межа такого компромісу суттєво залежить від змісту задачі, що розв’язується.

• Розв’язування теоретичних та практичних задач з використанням математичних моделей сигналів.

• Вивчення математичної моделі сигналу, як самостійного об’єкта дослідження.

• Вдосконалення математичної моделі сигналу.

В загальному розумінні сигнал є функціональною залежністю однієї фізичної величини від іншої.

В якості математичних моделей сигналів використовуються функції однієї та багатьох змінних, вектор-функції та матриці.

В першу чергу, ми будемо розглядати сигнал як функцію деякої змінної S в залежності від часу t (рис. 2.1): .

2.2. Типові сигнали

В цифровій обробці сигналів широко використовують типові сигнали, з допомогою яких здійснюють аналіз структури більш складних сигналів, визначають характеристики лінійних та нелінійних систем, здійснюють основні операції ЦОС, тощо. Тому ці типові сигнали ще називають еталонними або тестовими.

Серед неперервних (аналогових) сигналів еталонним, в першу чергу, є гармонічний сигнал та комплексно-експоненціальний сигнал . Ці сигнали теоретично нескінченної тривалості. Серед сигналів скінченної дії широко застосовуються імпульси різної форми. Послідовність імпульсів відноситься до кусково-неперервних сигналів. Неперервність та гладкість таких сигналів забезпечується на окремих інтервалах часу. 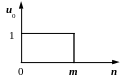Найпростішими кусково-неперервними сигналами є функція знаку та функція одиничного стрибка . 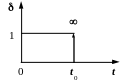До останньої примикає особлива дельта-функція , яка є дискретною функцією, що визначена в одній точці, при значенні аргументу t = 0. Серед дискретних сигналів, в першу чергу, вкажемо на дискретну гармоніку, цифровий одиничний стрибок та цифровий одиничний імпульс .

Аналітичні вирази та графіки сигналів , , та наведені в таблиці 2.1. В таблиці також відображається зв’язок функцій та , а також функцій та . Таблиця складена таким чином, що в лівій частині міститься інформація про функції та , а в правій – про їх дискретні аналоги та . В таблиці розкривається властивість одиничного стрибка та його аналога цифрового одиничного стрибка як функцій вмикання. Також розкривається пінцетна фільтрова властивість дельта-функції та її дискретного аналогу цифрового одиничного імпульсу .

2.3. Типові сигнали

В

S

першу чергу вияснимо, як змінюється аналітична форма сигналу при зміщенні початку відліку осі часу на величину τ. Нехай початок відліку часу співпадає з початком дії імпульсу (рис. 2.2) і при цьому аналітична форма імпульсу задана. При зміні початку відліку вправо на величину τ, тобто в точку О₁ графік функції не зміниться, але зміниться значення аргументу. Аналітична форма сигналу набуває вигляду . При зміщенні початку відліку вліво на величину τ, одержимо точку О₂, а аналітична форма сигналу прийме вигляд .

τ

S(t)

T_S

0

t

S₁=S(t + τ)

)

О₁

)

t

–τ

T_S – τ

S₂=S(t – τ)

)

S

τ

t

τ

T_S + τ

О₂

)

Рис. 2.2. 

Таблиця 2.1

Функція і та їх дискретні аналоги і

Функція одиничного стрибка	Цифровий одиничний стрибок
Дельта-функція	Цифровий одиничний імпульс
при умові, що .
Зв’язок та	Зв’язок та
; .	; .

Продовження таблиці 2.1

як функція вмикання	як функція вмикання
.	.
.	.
Фільтрова властивість	Фільтрова властивість
	.

Тепер не будемо міняти системи відліку, а будемо зміщувати імпульс на величину τ (рис. 2.3). Зміщення сигналу вправо в сторону запізнення на величину τ рівносильне зміщенню системи відліку вліво, а тому . Зміщення сигналу вліво в сторону випередження на величину τ рівносильне зсуву системи відліку вправо, тому .

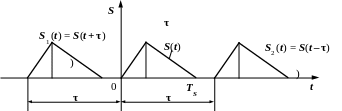
Рис. 2.3. 

Як і в попередньому випадку зміщення τ розглядається як додатна величина, тобто як відстань.

Досить часто, особливо при аналітичних викладках, зміщення τ зручно розглядати як алгебраїчну величину: τ додатна при зміщенні сигналу у додатному напрямку осі t (при запізненні) та τ від’ємне при зміщенні сигналу у від’ємному напрямку осі t (при випередженні). Тоді, незалежно від знаку зміщення τ аналітична форма сигналу завжди однакова: , що досить зручно (рис. 2.4).

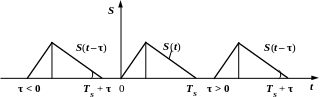
Рис. 2.4. 

При цифровій обробці сигналів досить часто замість роботи в реальному часі переходять до обчислень в умовному машинному часі з тактом, що дорівнює періоду дискретизації T. При цьому зміщення на m тактів в межах вибірки рухають від її початку в додатному напрямку, тобто зміщення m вважають додатною величиною, розглядаючи його як відстань. На рис. 2.5 зображені дискретні імпульси x(n) та його копії як з випередженням: , так і з запізненням: .

x

x₁ = x(n + m)

)

x(n)

x₂ = x(n – m)

)

– m

n

0

k – m

k + m

m

k

m

m

Рис. 2.5. 

Аналітичні вирази цих сигналів можна записати наступним чином:

Все викладене в цьому параграфі має відображення в таблиці 2.1 і буде використовуватись далі, особливо при виконанні основних операцій: кореляцій та згортки.