2.7. Залежність скалярного добутку сигналів від їх норми

Норму сигналу як його кількісну характеристику можна ввести по-різному.

Якщо норму сигналу ввести як корінь квадратний із його повної енергії:

, (2.24)

то скалярний добуток двох сигналів визначається формулою (2.14), а відстань та кут між двома сигналами визначають відповідно формулами (2.11) та (2.13). Раніше саме таким найпростішим чином вводили норму. Але при цьому можна працювати лише з тими сигналами, що мають скінчене значення енергії. За межами кількісної оцінки залишаються сигнали з нескінченим значенням енергії. Нескінчену енергію має, наприклад, гармоніка, яка широко використовується як еталонний сигнал.

Щоб розширити коло нормованих сигналів, в якості норми беруть середньоквадратичне значення сигналу:

, (2.25)

де середня потужність деяких нескінчених сигналів може бути знайдена згідно формул (2.18) чи (2.19), при умові, що їх інтеграли існують, навіть коли інтеграл (2.16) нескінчений.

Кут між сигналами не повинен залежати від вибору норми. Тому повинна виконуватись рівність:

.

Це означає, що при нормі скалярний добуток двох сигналів дорівнює

,

а при нормі скалярний добуток двох сигналів визначається формулою:

. (2.26)

При цьому маємо інваріантну форму визначення кута між сигналами

. (2.27)

Для імпульсів простіше вводити норму згідно (2.24), а в загальному випадку її вводять згідно (2.25). Саме тому, хоча вибірка є обмеженим в часі сигналом, як правило, її норма визначається формулою

. (2.28)

2.8. Практична частина

Приклад 2.1. Сигнал має математичну модель:

Дайте графічне зображення сигналу та запишіть математичну модель сигналу у вигляді одного аналітичного виразу.

Розв’язування. Зобразимо заданий сигнал графічно (рис. 2.8).

Згідно заданій математичній моделі бачимо, що сигнал є кусково-неперервною функцією, що складається із трьох кусків, при умові, що сигнал необмежений в часі. Його можна розглядати і як прямокутний імпульс на інтервалі .

Рис. 2.8. 

З допомогою функції включення (функції одиночного стрибка) математичну модель сигналу запишемо в вигляді одного аналітичного виразу:

.

Приклад 2.2. Дано графічне зображення сигналу (рис. 2.9). Записати математичну модель в аналітичній формі як кусково-неперервну функцію, а потім у вигляді одного аналітичного виразу.

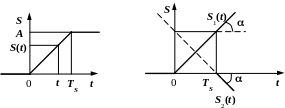
Рис. 2.9.  Рис. 2.10. 

Розв’язування. Функція кусково-неперервна, що має три характерні ділянки, аналітичні вирази яких мають вигляд:

Рівняння на відрізку можна одержати із пропорції .

Задане графічне зображення (рис. 2.10) сигналу при подамо як суму двох лінійних сигналів та з однаковими за модулем, але різним за знаком значенням кута  (рис. 2.10).

Визначимо функції та , використовуючи функцію вмикання:

, ;

, .

Знаходимо функцію :

.

П риклад 2.3. Задано трикутний імпульс напруги з амплітудою U. Тривалість імпульсу (рис. 2.11). Обчислити енергію та відповідну норму заданого сигналу U(t).

Рис. 2.11.

Розв’язування. Математичну модель сигналу запишемо у вигляді аналітичного виразу:

Енергія сигналу (імпульсу):

.

Відповідна даній енергії норма імпульсу

.

Приклад 2.4. Визначити енергію та відповідну норму радіоімпульсу з прямокутною формою огинаючої. Радіоімпульс існує на інтервалі і описується функцією .

Довідка. Для здійснення передачі сигналу на значні відстані без суттєвих втрат інформації, його помножують на високочастотну гармоніку , тобто передають у вигляді високочастотної гармоніки із змінною амплітудою . Після передачі сигналу , який називають радіоімпульсом, його фільтрують і знов одержують сигнал , який називають відеоімпульсом. Проілюструємо це у вигляді графіків (рис. 2.12).

S

t₀+T_S

t

0

t₀

відеоімпульс

радіоімпульс

Рис. 2.12. 

Розв’язування. Так як радіоімпульс має сталу амплітуду U₀, то він має прямокутну форму, що визначається огинаючими U = ±U₀.

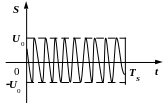
Рис. 2.13.

Визначимо енергію радіоімпульсу:

.

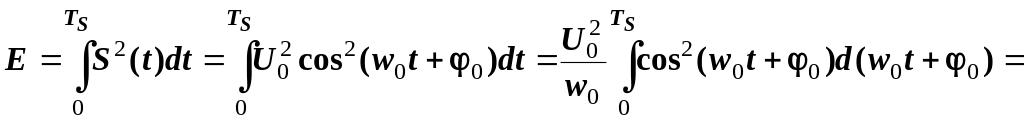
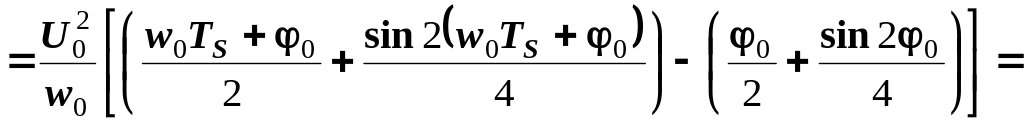
Тут була здійснена заміна , тому , а . Якщо w₀ достатньо велике, таке що , то енергія радіоімпульсу

.

Тобто значення енергії радіоімпульсу при високій частоті несучої гармоніки практично не залежить від початкової фази та самого значення w₀. Звідси особлива роль енергетичної характеристики.

Норма радіоімпульсу

.

Зауваження. При визначенні інтегралу ми скористались його табличним значенням.

Корисно запам’ятати, що

;

.

Приклад 2.5. Задано відео імпульс у вигляді півперіоду синусоїди на відрізку , висота якого U (рис. 2.14).

Підібрати амплітуду А прямокутного імпульсу тієї ж тривалості T_S так, щоб відстань між двома сигналами та була мінімальною. Знайти при цьому кут між сигналами.

Рис. 2.14. 

Розв’язування. Аналітичну форму сигналів запишемо у вигляді

При визначенні на інтервалі була використана пропорція

.

Знайдемо квадрат відстані між сигналами:

.

Обчислимо кожний із трьох інтегралів окремо.

.

.

.

Отже,

. (2.29)

Умова мінімальної відстані в залежності від А має вигляд

.

Звідки

. (2.30)

Визначимо , підставивши (2.29) в (2.30).

.

.

Знайдемо енергію імпульсів:

;

;

.

Визначимо норми сигналів:

; .

Знайдемо кут між сигналами

.

Отже, .

Приклад 2.6. Дано дві тривимірні вибірки: x (n) = (4; −4; 7) та y (n) = (3; −2; 6). Знайти відстань і кут між вибірками та складову вибірки х в напрямку вибірки у.

Розв’язування. Вибірку ототожнюємо із тривимірними векторами. Визначимо норми вибірок:

.

.

Знайдемо відстань між вибірками як їх метрику

.

Скалярний добуток вибірок

.

Знайдемо кут між вибірками

.

Одиничний вектор в напрямку вибірки y:

.

Тому, складова вибірки x в напрямку вибірки y дорівнює:

.

Приклад 2.7. Сигнали та прямокутні відеоімпульси з амплітудами А₁ та А₂, тривалості Т₁ та Т₂ зображені на рис. 2.15. Обидва сигнали одночасно відрізняються від нуля на інтервалі . Визначити кут між сигналами.

Рис. 2.15. 

Розв’язування. Спочатку знайдено скалярний добуток сигналів:

.

Визначимо норми сигналів:

;

.

Визначимо кут між сигналами:

.

Як бачимо, величина кута між прямокутними імпульсами не залежить від їх амплітуд А₁ та А₂.

Приклад 2.8. Задані два сигнали: прямокутний відеоімпульс та експоненціальний відеоімпульс Вважаючи тривалість Т прямо­кутного імпульсу фіксованою, визначити величину метрики .

Розв’язування. Знайдемо квадрат відстані між сигналами:

.

.

.

.

Отже,

.

Величина метрики як відстань між сигналами дорівнює

.