1.5. Показникова форма комплексного числа

В теорії комплексних чисел використовуються тригонометричні функції комплексної змінної, наприклад, sin z, cos z тощо, а також показникові функції: , тощо. Формула Ейлера встановлює відповідність між певними тригонометричними та показниковими функціями комплексного числа z.

У загальному випадку формула Ейлера має вигляд:

. (1.37)

Якщо у формулі (1.37) зробити заміну i = i, то матимемо:

. (1.38)

Додавши формули (1.37) та (1.38), одержимо:

. (1.39)

Віднявши від рівняння (1.37) рівняння (1.38), матимемо:

. (1.40)

Формули (1.39) та (1.40) мають важливе практичне значення. Ми досить часто будемо вживати їх при переводі тригонометричних функцій дійсної змінної в поле комплексних змінних.

При заміні z =  тригонометричні функції комплексної змінної правої частини формули (1.37) стають функціями дійсної змінної, а ліва частина залишається функцією комплексної змінної. Формула Ейлера набуває вигляду

. (1.41)

Права частина рівняння (1.41) є тригонометричною формою будь-якого комплексного числа z, модуль якого . При довільному значенні аргумента  це рівняння одиничного кола. Отже, функція є теж рівнянням одиничного кола в показниковій формі.

Ця формула дозволяє будь-яке комплексне число z представити в показниковій формі:

. (1.42)

Або остаточно

. (1.43)

де   аргумент комплексного числа z.

Для більш глибокого сприйняття формули Ейлера (1.41) дамо основний зміст її доведення. Для цього скористаємося розкладом функції в ряд Тейлора:

Розкладемо в ряд Тейлора функції cos  та sin , що стоять в правій частині (1.41), при а = 0.

Аналогічним чином розкладемо в ряд Фур’є комплексну функцію . Строге доведення такого розкладу цієї функції в комплексний ряд Тейлора дається в теорії функцій комплексної змінної. Ми це здійснимо формально, посилаючись на теорію.

.

Отже, ми підтвердили вірність формули Ейлера.

Згідно показникової форми (1.43) будь-яке комплексне число z знаходиться на колі радіуса і має кутову координату (фазу) . Отже, рівняння (1.43) можна розглядати як рівняння кола радіуса на комплексній площині.

При одержимо рівняння одиничного кола:

.

y

(1.44)

Саме на одиничному колі фіксується значення аргументу φ у вигляді числа , при цьому має місце взаємно-однозначна відповідність .

На одиничному колі (рис. 1.8) зображено шість комплексних чисел:

; ; ;

; ; .

Рис. 1.8. 

• Показникова (експоненціальна) форма комплексного числа зручна для здійснення множення, ділення, піднесення до степеня, добування кореня, вона спрощує операції диференціювання та інтегрування.

Дійсно, якщо , , то

. (1.45)

Отже,

, (1.46)

де модуль , а аргумент .

Ділення числа на число відповідає формулі:

. (1.47)

Важливим є розширення показникової функції до більш загальної функції .

Виходячи з того, що одержимо:

. (1.48)

Таким чином, якщо , то модуль та аргумент функції відповідно дорівнюють:

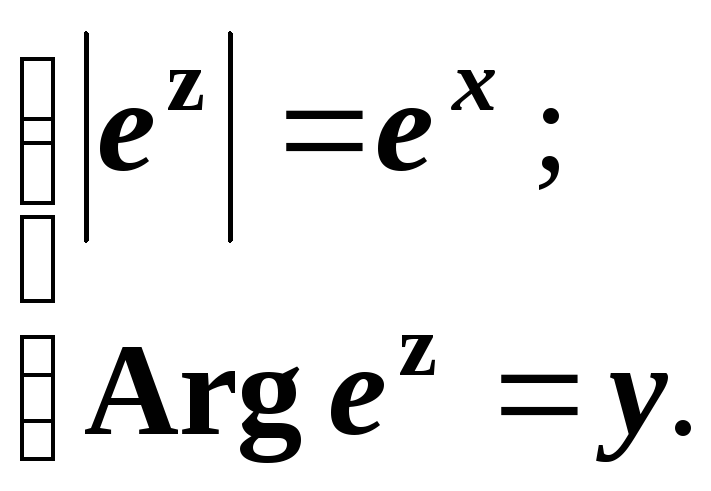(1.49)

Функція  періодична функція і має період 2πі.

Дійсно

(1.50)

Зокрема,

(1.51)