
- •Практикум 1 Комплексні числа та дії над ними
- •1.1. Теоретичні та довідкові дані
- •1.2. Алгебраїчна форма комплексного числа
- •1.3. Геометрична форма комплексного числа
- •1.4. Тригонометрична форма комплексного числа
- •1.4.1. Множення та ділення комплексних чисел
- •1.5. Показникова форма комплексного числа
- •1.5.1. Спряжені комплексі числа
- •Висновки
- •1.6. Приклади
- •1.7. Індивідуальні завдання
- •1.8. Приклади розв’язування індивідуальних задач
- •1.9. Контрольні запитання
1.4. Тригонометрична форма комплексного числа
Користуючись формулами (1.13), можна будь-яке комплексне число, що відмінне від нуля, представити в тригонометричній формі:
z = x + yi = r cos + i rsin = r (cos + i sin ). (1.23)
Таким чином, остаточно маємо:
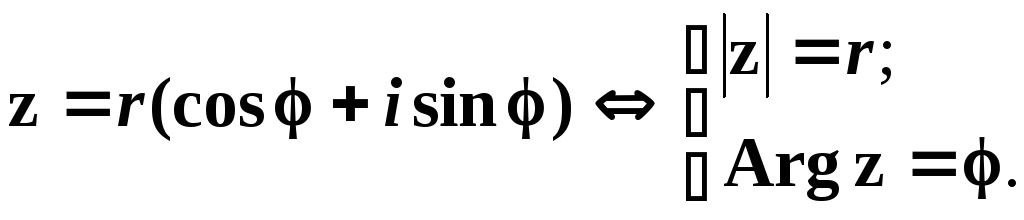 (1.24)
(1.24)
Якщо таке, що – < ≤ , то = arg z.
Тригонометрична форма (1.24) комплексного числа має такі особливості:
множник перед дужками як радіус обов’язково додатне число (r > 0);
алгебраїчне значення аргументу однакове за величиною та знаками для синусу і косинусу;
доданки cos та sin записуються зі знаком плюс, хоча можуть бути додатні або від’ємні в залежності від значення .
Тригонометрична форма комплексного числа зручна для здійснення множення та ділення комплексних чисел, піднесення до степеня n та добування кореня степеня n комплексного числа.
1.4.1. Множення та ділення комплексних чисел
Здійснимо множення двох комплексних чисел, що задані в тригонометричній формі, як множення двох многочленів:
![]()
![]()
![]()
Отже,
![]() (1.25)
(1.25)
Або
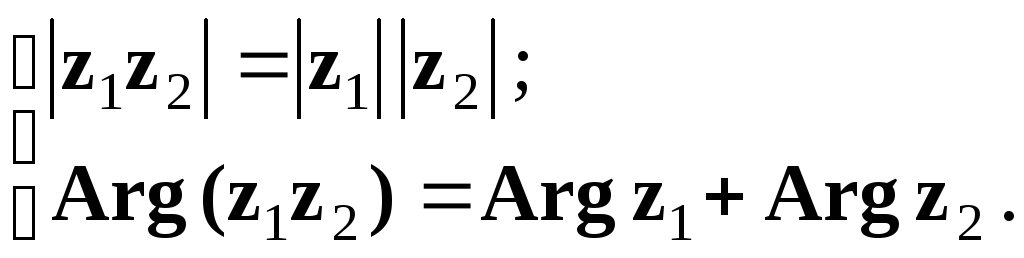 (1.26)
(1.26)
Модуль добутку комплексних чисел дорівнює добутку їх модулів, а аргумент – сумі їх аргументів (рис. 1.6, а).
Здійснивши аналогічним чином ділення комплексного числа
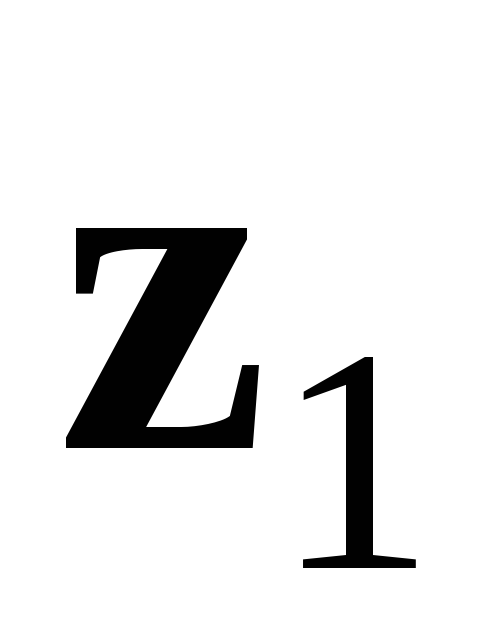 на комплексне число
на комплексне число
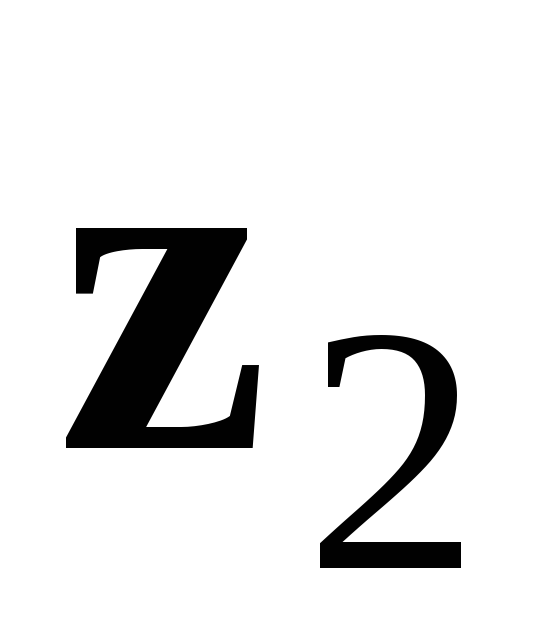 за умов що
за умов що ≠ 0,
одержимо:
≠ 0,
одержимо:
![]() (1.27)
(1.27)
Тобто
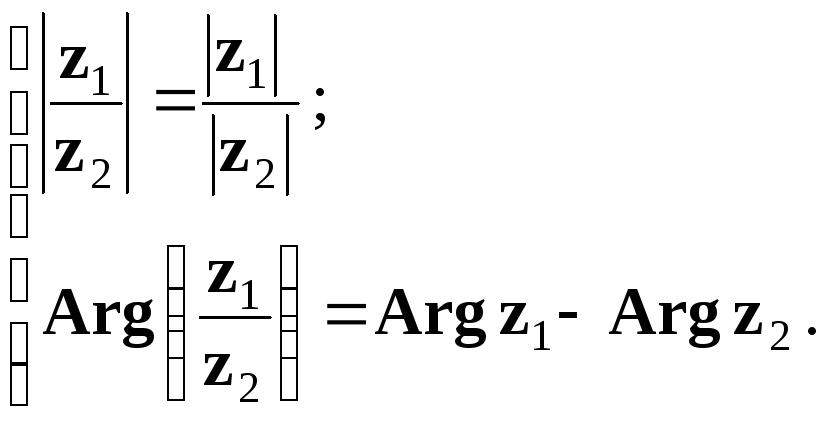 (1.28)
(1.28)
Модуль частки від ділення комплексного числа
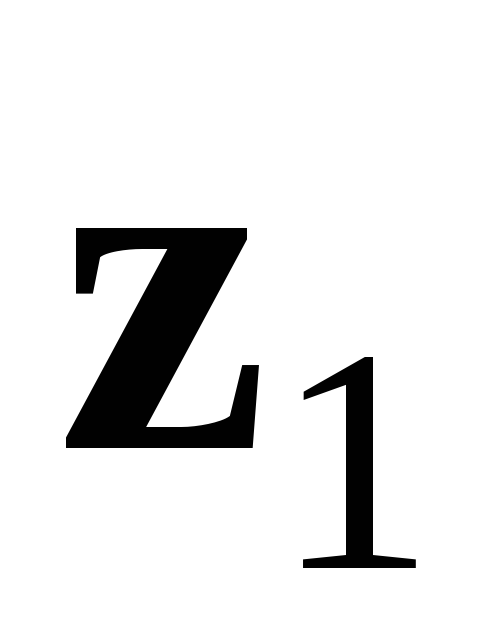 на
комплексне число
на
комплексне число
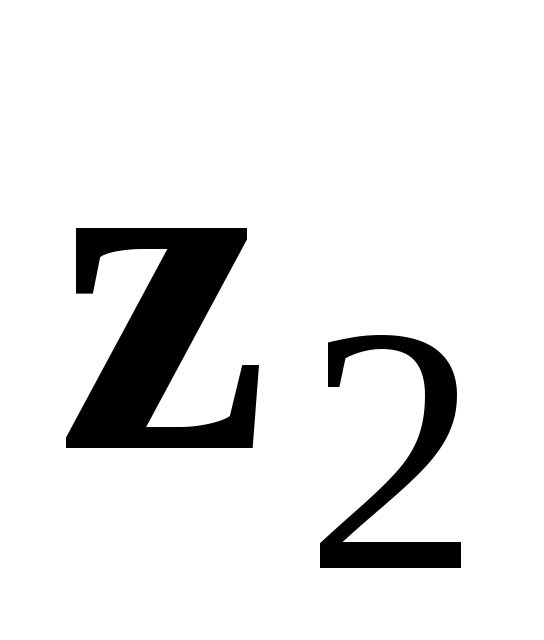 дорівнює частці їх модулів, а аргумент
– різниці аргументів діленого і дільника
(рис. 1.6, b).
дорівнює частці їх модулів, а аргумент
– різниці аргументів діленого і дільника
(рис. 1.6, b).
y
y
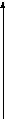
z = z1z2
z1



z2
1+2
і
і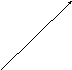

z2
1 z = 



![]()


2
z1
2
1–2





1
x
x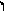

0
0
a)
b)
Рис. 1.6. Множення та ділення комплексних чисел
Рис. 1.5
Тригонометрична форма дозволяє досить легко здійснювати множення та ділення чисел.
Так як , то множення числа z на і зводиться до повороту вектора z на кут π/2 проти годинникової стрілки, а ділення z на і зводиться до повороту вектора z на кут π/2 за годинниковою стрілкою.
1.4.2. Формула Муавра
Піднесення дійсного числа до степеня n є частковим випадком дії множення:
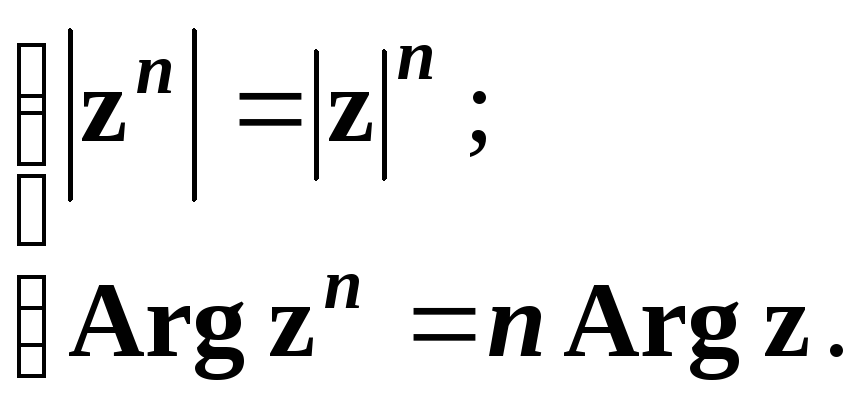 (1.29)
(1.29)
При
![]() має місце формула Муавра:
має місце формула Муавра:
(cos + i∙sin )n = cos n + isin n. (1.30)
Формули
(1.29)
та (1.30)
вірні і для від’ємних n,
так як
![]() .
.
1.4.3. Добування кореня степеня n
Добути
корінь степеня n
із числа z
означає знайти таке число
![]() ,
для якого
(z ≠ 0),
тобто
,
для якого
(z ≠ 0),
тобто
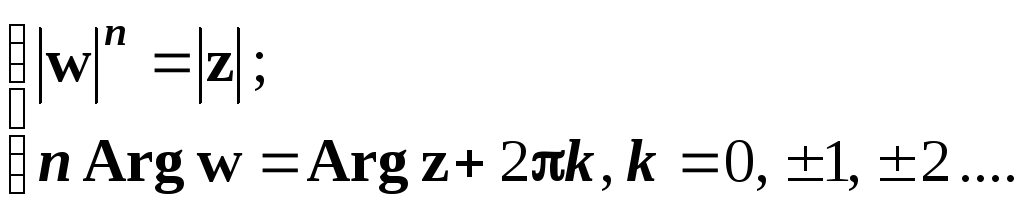 (1.31)
(1.31)
Тут враховано те, що на площині z аргумент зображується з точністю до цілого числа повних обертів 2πk. Тому, при добуванні кореня цей доданок дозволяє не втратити жодного розв’язку, тобто кореня.
Якщо комплексні числа z та w записати в тригонометричній формі:
z = r (cos + i sin ), (1.32)
w = (cos + i sin ), (1.33)
то згідно (1.31)
![]() ,
(1.34)
,
(1.34)
![]() .
(1.35)
.
(1.35)
Отже,
модулі всіх коренів однакові. Значення
фазового кута
![]() залежить
від значення k:
залежить
від значення k:
![]() ,
,
![]() .
(1.36)
.
(1.36)
При
k ≥ n
значення
![]() ,
а отже і значення коренів повторюються
з точністю до цілого числа повних
обретів. Корені з кроком
,
а отже і значення коренів повторюються
з точністю до цілого числа повних
обретів. Корені з кроком![]() рівномірно розташовані по колу радіуса.
Початкове значення аргументу кореня
при k = 0
дорівнює
рівномірно розташовані по колу радіуса.
Початкове значення аргументу кореня
при k = 0
дорівнює
![]() .
Звідси має місце наступний алгоритм
знаходження коренів (рис. 1.7):
.
Звідси має місце наступний алгоритм
знаходження коренів (рис. 1.7):
Визначаються модуль та аргумент числа z:
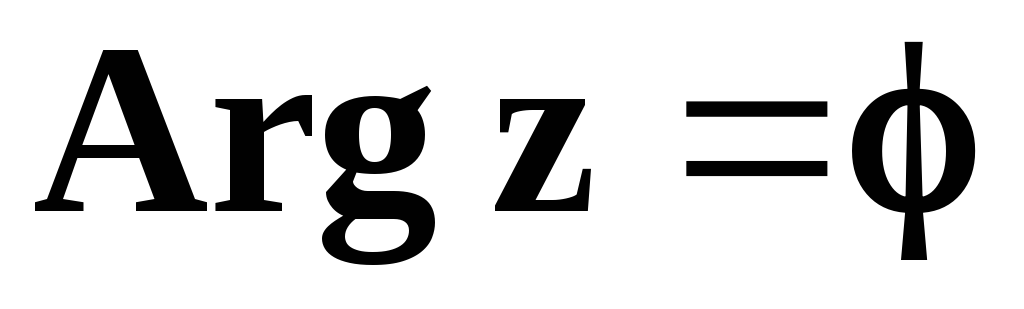 .
.Знаходиться модуль кожного кореня:
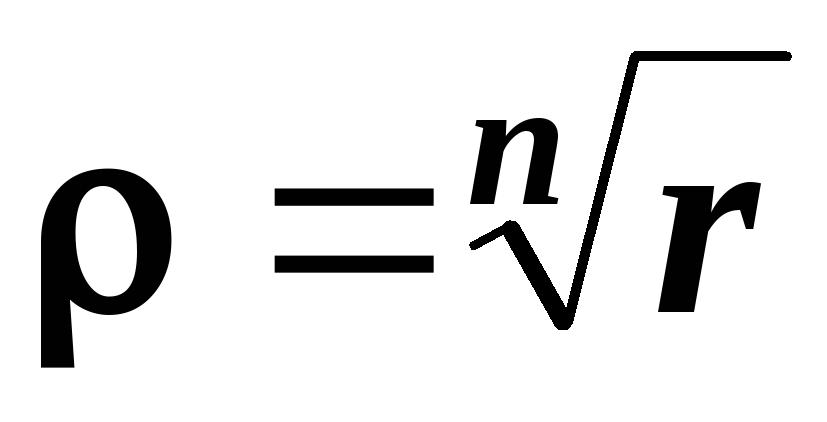 .
.Знаходиться аргумент нульового кореня:
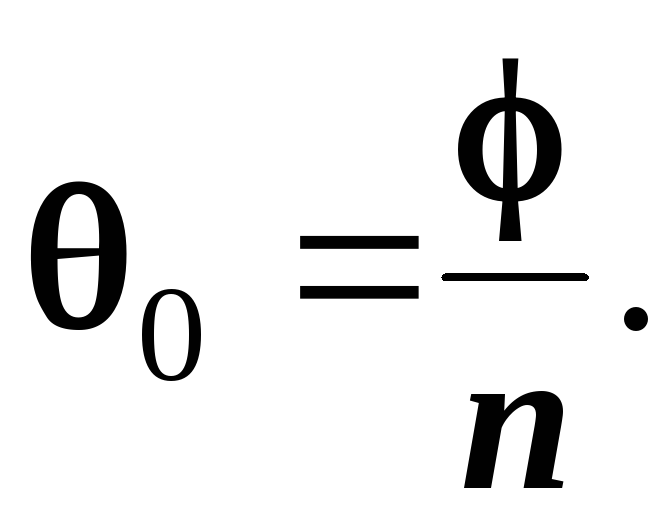
Визначається кутовий крок коренів:
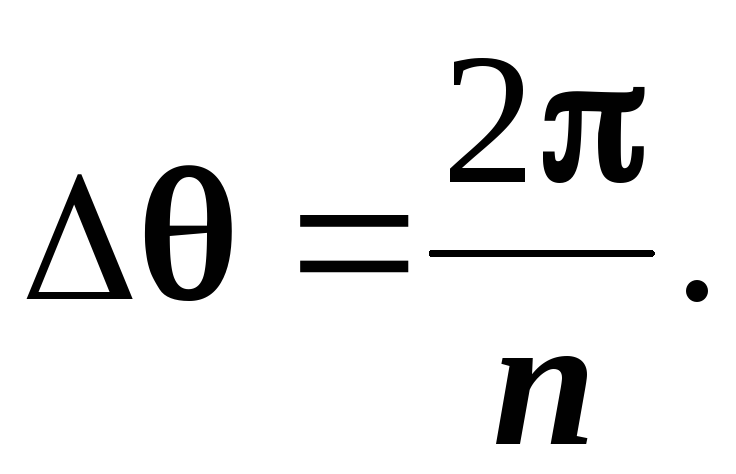
Визначається аргумент кожного кореня:
![]() ,
k = 0, 1, 2, …, n – 1.
,
k = 0, 1, 2, …, n – 1.
Визначаються в тригонометричній формі всі n корені числа z:
![]() ,
k = 0, 1, 2, …, n – 1.
,
k = 0, 1, 2, …, n – 1.
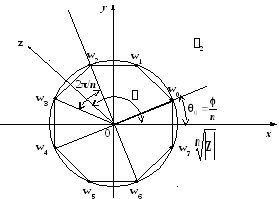


Рис. 1.7. Добування кореня степеня n
Зауважимо, що:
операція
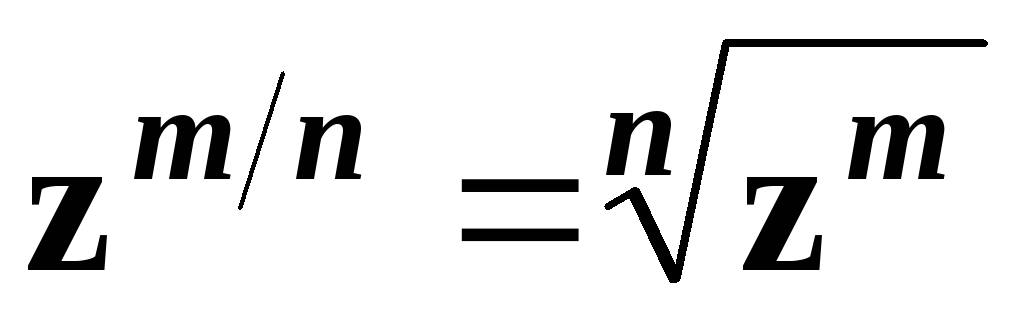 як послідовність операцій піднесення
до степеня m
та операцій добування кореня степеня
n
визначена для будь-яких цілих значень
m
i n;
як послідовність операцій піднесення
до степеня m
та операцій добування кореня степеня
n
визначена для будь-яких цілих значень
m
i n;у виразі
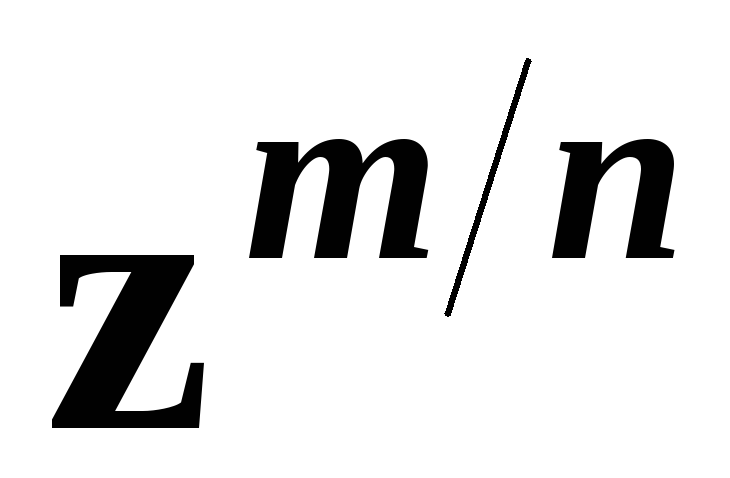 дріб
m/n
не
скорочується, навіть, якщо m
i n
мають спільні множники. Вираз
дріб
m/n
не
скорочується, навіть, якщо m
i n
мають спільні множники. Вираз
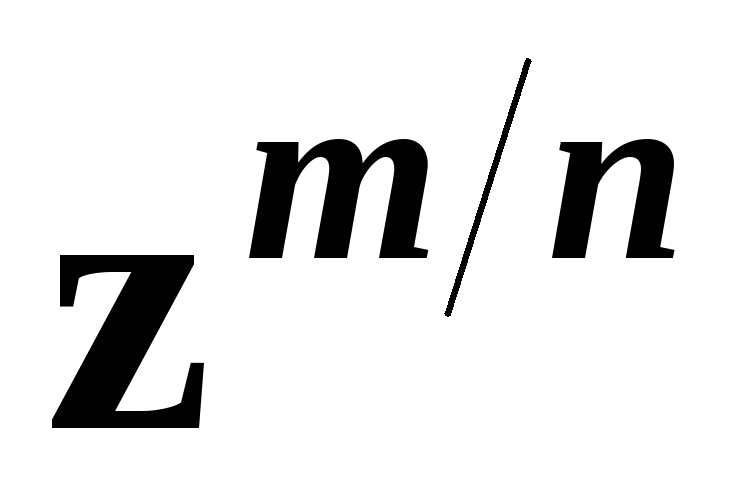 має
n
коренів. Наприклад, вираз
має
n
коренів. Наприклад, вираз
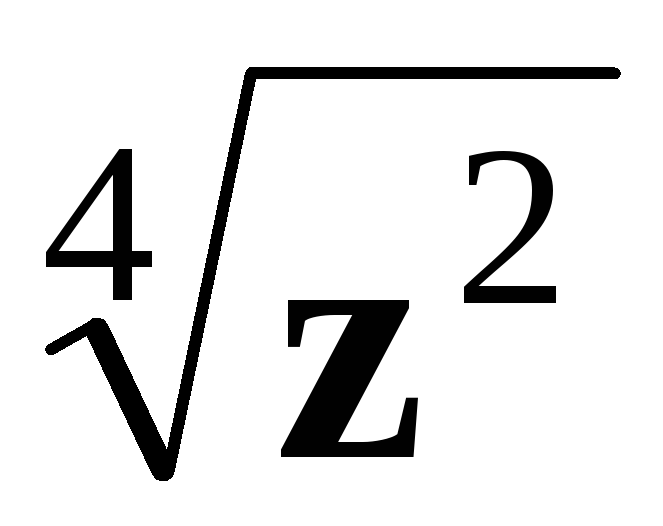 має
чотири корені, а вираз
має
чотири корені, а вираз
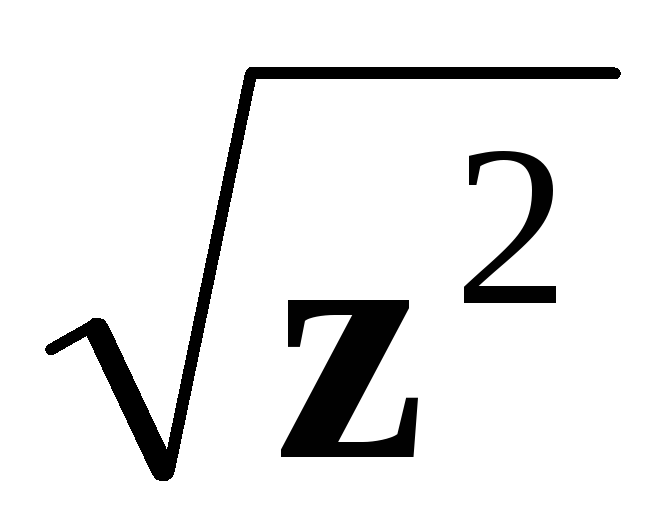
два корені.
два корені.
