
- •Молекулярна фізика та термодинаміка
- •6. Молекулярна фізика
- •6.1. Вступ
- •6.2. Імовірність та флуктуації
- •6.3. Ідеальний газ та його характеристики
- •6.3.1. Температура
- •2).Шкала Фаренгейта
- •3).Шкала температури Кельвіна
- •6.4. Енергія частинки ідеального газу
- •6.4.1.Теорема Больцмана про рівнорозподіл енергії. Енергія частинки
- •6.5. Внутрішня енергія ідеального газу
- •6.6. Молекулярно кінетична теорія для тиску
- •6.7. Ефективний діаметр та ефективний переріз розсіювання
- •6.8. Кінематичні характеристики ідеального газу
- •6.8.1. Статистичний розподіл частинок за напрямком руху
- •6.8.2. Число зіткнень частинки за одиницю часу
- •6.8.3. Середня довжина вільного пробігу
- •6.9. Розподіл Максвелла для частинок за швидкостями
- •6.9.1. Закон розподілу
- •6.9.2. Максимум густини розподілу
- •6.9.3. Середня арифметична швидкість
- •6.9. 4. Середня квадратична швидкість визначається як
- •6.9.5. Експериментальна перевірка розподілу Максвелла
- •6.10. Барометрична формула та розподіл Больцмана
- •6.10.1. Барометрична формула
- •6.10.2. Розподіл Больцмана
- •6.11. Розподіл Максвелла - Больцмана
- •6.11.1. Розподіл Максвелла за значеннями кінетичної енергії
- •6.11.2. Розподіл Максвелла - Больцмана
- •6.12. Явища переносу
- •6.13. Дифузія
- •6.14. Теплопровідність
- •6.15. Внутрішнє тертя
- •6.16. Контрольні питання
6.8.2. Число зіткнень частинки за одиницю часу
Число співударянь частинки із середньою швидкістю V при концентрації n за 1с дорівнює
![]() .
.
 Щоб
одержати цей вираз, розглянемо траєкторію,
що її опише частинка ідеального газу
за часdt.
Вона являє собою деяку ламану лінію, у
вузлах якої відбулися зіткнення з іншими
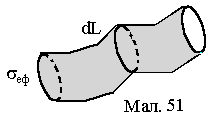
частинками. ЇЇ довжина становить dL=Vdt.
Побудуємо на цій ламаній, як на осі,
циліндр з основою, рівною ефективному
перерізу
Щоб
одержати цей вираз, розглянемо траєкторію,
що її опише частинка ідеального газу
за часdt.
Вона являє собою деяку ламану лінію, у
вузлах якої відбулися зіткнення з іншими
частинками. ЇЇ довжина становить dL=Vdt.
Побудуємо на цій ламаній, як на осі,
циліндр з основою, рівною ефективному
перерізу
![]() (див.Мал.51)). Приймаючи до уваги властивість
ефективного перерізу, можна стверджувати,
що розглядувана частинка обов’язково
співудариться з усіма нерухомими
частинками
(див.Мал.51)). Приймаючи до уваги властивість
ефективного перерізу, можна стверджувати,
що розглядувана частинка обов’язково
співудариться з усіма нерухомими
частинками
![]() ,
,
які знаходяться в циліндрі. Але частинки рухаються і тому замість швидкості V потрібно взяти відносну середню квадратичну швидкість Vв, яку розрахуємо так
![]() .
.
В записаному виразі
![]()
вектор відносної швидкості двох частинок.
З достатньою точністю можна покласти,
що
вектор відносної швидкості двох частинок.
З достатньою точністю можна покласти,
що
![]() ,
а
,
а
![]() тому, що кут
тому, що кут![]() між векторами
між векторами
![]() змінюється в межах від 00
до 1800
і
змінюється в межах від 00
до 1800
і
![]() .
В результаті маємо, що
.
В результаті маємо, що
![]() і число співударянь за час dt
дорівнює
і число співударянь за час dt
дорівнює
![]() ,
а число співударянь за одиницю часу
дорівнює
,
а число співударянь за одиницю часу
дорівнює
![]() .
.
За
нормальних умов частинка атмосфери з
![]() здійснює
здійснює
Z=3,11010 с-1.
6.8.3. Середня довжина вільного пробігу
Середня довжина вільного пробігу є середня відстань між двома послідовними співударяннями частинок, що рухаються рівномірно й прямолінійно. Величину можна обчислити, виходячи з того, що на довжині траєкторії dL=Vdt відбувається Zdt співударянь і тоді середня довжина вільного пробігу між співударяннями становить
![]() .
.
Приймаючи до уваги, що
![]() ,
можна записати
,
можна записати
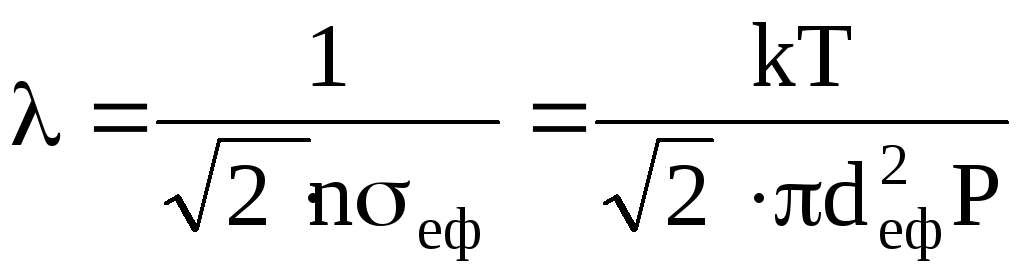 .
.
За
нормальних умов частинка атмосфери з
![]() має
має![]() .
.
6.9. Розподіл Максвелла для частинок за швидкостями
6.9.1. Закон розподілу
частинок ідеального газу за швидкостями визначає їх стаціонарний розподіл за швидкостями в умовах термодинамічної рівноваги й відсутності зовнішнього силового поля.
Розподіл частинок ідеального газу за абсолютними значеннями швидкостей V дослідив Максвелл. Він визначив, що число частинок, швидкості яких лежать в інтервалі (V; V + dV) представляється виразом
![]() ,
,
де
![]() загальне число частинок, а їх частка
загальне число частинок, а їх частка
![]() (1)
(1)
є ймовірністю такого розподілу із густиною
![]() .
(2)
.
(2)
В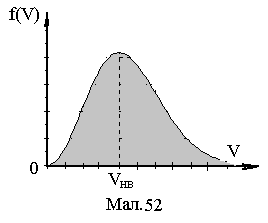 цьому виразі m
маса частинки, k
стала Больцмана, Т
температура. Стала нормування А
визначається так
цьому виразі m
маса частинки, k
стала Больцмана, Т
температура. Стала нормування А
визначається так
![]() .
(3)
.
(3)
Залежність (2) представлена на Мал.52.
Закон Максвелла можна
застосовувати і для скінчених малих
величин
![]() та
та![]()
![]() .
(4)
.
(4)
6.9.2. Максимум густини розподілу
f(V) знаходиться в точці V=Vнв (див.Мал.5), яка називається найбільш імовірною швидкістю і
![]() .
.
Дійсно,
![]() .
.
Прирівняємо похідну 0 і
знайдемо точку екстремуму
![]()
![]()
![]() ,
,
що й треба було довести.
Вираз
![]() значно спрощується, якщо ввести змінну
значно спрощується, якщо ввести змінну
![]() ,
тоді
,
тоді![]() ,
,![]() ,
,
![]()
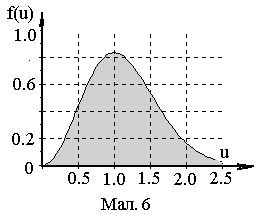 ,
,![]() .
.
Графік густини розподілу f(u) по u представлено на Мал.6. Максимум густини такого розподілу приходиться на u=1.
6.9.3. Середня арифметична швидкість
визначається як
![]() ,
,
для дискретних значень V та
![]() ,
,
для неперервних значень V.
Розрахунки середньої швидкості частинок ідеального газу за розподілом Максвелла дають
![]() =
=
![]() 1.
60
1.
60![]() .
(1)
.
(1)
Дійсно,
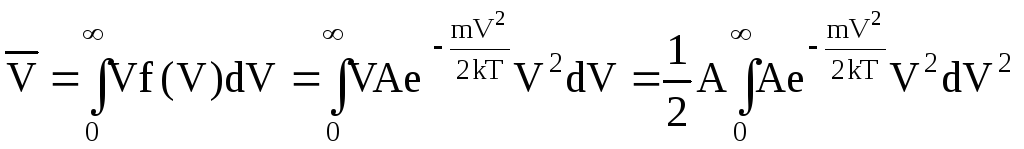
Зробимо заміну змінної
![]() ,
,![]() ,
,![]()
i тепер
![]()
![]() .
(2)
.
(2)
Ми проінтегрували
![]()
по частинам:
![]() =
=![]() +
+![]() =0-
=0-![]() =1.
=1.
6.9. 4. Середня квадратична швидкість визначається як
с =
![]() ,
(1)
,
(1)
де
![]() .
Розрахуємо (1) за допомогою теореми
Больцмана про рівнорозподіл енергії
за ступенями свободи для вільної
частинки. Згідно цієї теореми середня
кінетична енергія теплового руху
частинки з масоюm
дорівнює
.
Розрахуємо (1) за допомогою теореми
Больцмана про рівнорозподіл енергії
за ступенями свободи для вільної
частинки. Згідно цієї теореми середня
кінетична енергія теплового руху
частинки з масоюm
дорівнює
![]()
і звідси
с =
![]() .
.
