6.5. Внутрішня енергія ідеального газу

Внутрішня теплова енергія ідеального газу. Якщо частинка має масу m₀, а газ має - m, то він має частинок, а його внутрішня енергія теплового руху дорівнює

,

де молярна маса, або

U = . (4)

Якщо врахувати, що стан ідеального газу визначається рівнянням Клапейрона-Менделєєва

,

то вираз для внутрішньої енергії прийме вид

. (5)

6.6. Молекулярно кінетична теорія для тиску

Якщо на плоску поверхню площею S з нормаллю діє сила, то під тиском Р розуміють границю відношення величини нормальної складової сили доS

.

Співударяючись із стінками посудини, в якій знаходиться ідеальний газ, частинки створюють середню силу <F> дії на одиницю поверхні, тобто створюють тиск Р. Як показав Максвел, цей тиск не залежить від того, що співударяння з стінками пружні чи не пружні. Знайдемо тиск газу у наближенні абсолютно пружного співударяння частинок із стінкою. 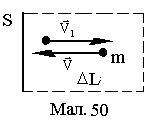Для цього покладемо, що частинка перед ударом має швидкість , котра направлена перпендикулярно поверхні стінки (див.Мал.50). Після абсолютно пружного співударяння, частинка змінить напрямок швидкості на протилежний і її приріст імпульсу складатиме

Якщо концентрація частинок дорівнює n, то у поперечному напрямку до стінки буде рухатися n/6 частинок (маємо один з 6 напрямків декартових координат). За час t стінки досягнуть усі частинки, котрі знаходяться на відстані від неї L=Vt. Якщо розглянути одиничну поверхню S, то за цей час із стінкою співударяться

N=nSL/6. (1)

частинок і стінці буде передано імпульс

P=Np=2mVnSVt/6=nmV²t/3. (2)

За другим законом Ньютона на стінку буде діяти сила

.

Знайдемо середню силу <F>=n<mV²>/3, що діє на стінку одиничної площі

S і фактично є тиском Р, який створюється частинками газу, тобто

Р=n<mV²>/3.

Величина <mV²>/2 є середньою кінетичною енергією теплового руху частинки. Якщо газ одноатомний з і=3, то, враховуючи 6.4.2. (3), одержимо

<mV²>=3kT

і тоді

P=nkT. (3)

6.7. Ефективний діаметр та ефективний переріз розсіювання

Знаходячись у неперервному тепловому русі частинки газу співударяються, змінюючи напрямок руху і швидкість. У цьому питанні важливим для розгляду розсіювання є оцінка динамічного розміру частинки.

Ефективним діаметром частинок ідеального газу є найменша відстань між центрами двох частинок, які здійснюють центральний пружний удар. За порядком величини

.

Нижче в Таблиці 1 наведені значення ефективного діаметра для деяких газів.

Таблиця 1. Значення ефективного діаметра деяких молекул

Газ	Азот	Аргон	Кисень	Водень	Гелій
d·1010 м	3,75	3,64	3,61	2,74	2,18

Ефективний газокінетичний поперечний переріз _еф дорівнює площі круга з радіусом

.

Властивістю ефективного перерізу є те, що дві частинки, які одночасно проходять через , обов'язково співударяються.

6.8. Кінематичні характеристики ідеального газу

6.8.1. Статистичний розподіл частинок за напрямком руху

Хаотичність теплового руху n частинок ідеального газу означає їх рівнорозподіл руху за напрямками швидкостей, а саме: усі напрямки теплового руху рівно ймовірні. Якщо в простір частинок увести декартову систему координат із 3-ма осями  x, y, z і 6-ма напрямками по ним (), то в кожному з них рухається

частинок. Наприклад, якщо частинки мають середню швидкість теплового руху V, то в додатному напрямку осі ОХ через перпендикулярну до неї площину S за час dt пройдуть всі частинки, що знаходяться на відстані dL = V·dt в об'ємі dLS, а їх загальне число становить

.