3. Інтервальні оцінки

Необхідно оцінити невідомі математичні сподівання M[X] i M[Y] генеральних сукупностей Х, У за допомогою довірчого інтервалу з надійністю 0,95.

(3.1)

де 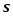- «виправлене» вибіркове середнє квадратичне відхилення, знаходять по таблиці додатка 2 за заданими і .

Отже = 0,95, n=50.користуючись таблицею значень 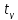(додаток 2), знаходимо

Ми маємо нормально розподілену кількісну ознаку генеральної сукупності. За вибіркою n=50 знайдені вибіркове середнє (з пункту 2):

для вибірки Х :

для вибірки Y :

і “виправлене ” середнє квадратичне відхилення :

(3.2)

D_в ми теж візьмемо з попереднього завдання:

для вибірки Х: 0.925

для вибірки У: 0.586.

і ці значення підсталяємо в формулу(3.2). Отримуємо S:

для вибірки Х : 0,97

для вибірки Y : 0,77

Знайдемо довірчі інтервали для вибірoк Х та Y:

Підставляємо всі значення в формулу (3.1) і отримуємо:

для вибірки Х :

-0,26˂a˂0,29

для вибірки Y :

-0,19˂a˂0,25

Висновок: Ми оцінили невідомі математичні сподівання М[Х] і M[У] генеральних сукупностей Х і У за допомогою довірчого інтервалу з надійністю 0,95. Для вибірки Х з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,26 < a < 0,29. Для вибірки Y з надійністю -0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,19 < a < 0.25.

4. Перевірка гіпотези про рівність дисперсій генеральних сукупностей

Запропонуємо просту гіпотезу про рівність дисперсій генеральних сукупностей H₀: D(X) = D(Y) при конкуруючій гіпотезі H₁: D(X) ≠ D(Y). Перевіримо запропоновані гіпотези при рівні значущості α = 0,1.

Для того, щоб при заданому рівні значущості α перевірити нульову гіпотезу H₀: D(X) = D(Y) про рівність генеральних дисперсій нормальних сукупностей при конкуруючій гіпотезі H₁: D(X) ≠ D(Y), потрібно обчислити емпіричне значення критерію F_емп як відношення більшої виправленої дисперсії до меншої

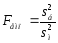
(4.1) де s²_б – більша виправлена дисперсія, s²_м – менша виправлена дисперсія.

Ми маємо великі вибірки n₁ = n₂ = 50 . Отже за виправлені вибіркові дисперсії можна взяти вибіркові дисперсії, які ми знайшли в пункті 2.

Отже, маючи вибіркові дисперсії двох вибірок можна стверджувати

s²_б ≈ D_в(X) =0,94 (4.2)

s²_м ≈ D_в(Y) =0,6 (4.3)

Підставимо значення (4.2) та (4.3) в формулу (4.1), отримаємо

F_емп= 1,58

За умовою задачі, конкуруюча гіпотеза має вигляд H₁: D(X) ≠ D(Y), тому критична область – двостороння.

По таблиці Фішера-Снедекора, по рівню значущості, що в двічі менший за заданий, тобто при α/2 = 0,1/2 = 0,05, та кількістю степенів свободи k₁ =50-1=49 ,k₂ =50-1=49 знаходимо критичну точку F_кр(α/1; k₁, k₂) = (0,05; 49, 49) = 1,6.

Так як критичний критерій менший за емпіричний F_емп > F_кр (1,66 < 2,5978), то немає підстави відхилити запропоновану гіпотезу, тобто нульова гіпотеза приймається.

Висновок: Результати показують, що вибіркові виправлені дисперсії двох вибірок відрізняються суттєво. Враховуючи, що вибіркові виправлені дисперсії є незміщеними оцінками генеральних дисперсій, то це ж стосується і генеральних дисперсій.

5. Побудова нормальних кривих за дослідними даними.

Для побудови нормальної кривої необхідно визначити емпіричні і теоретичні

(вирівнюючі) частоти.

Емпіричними частотами називають частоти n_i, які фактично спостерігаються Вирівнюючими (теоретичними) називають частоти n_i, які знаходяться

теоретично (обчисленням):

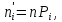(5.1)

де n – кількість спостережень;

P_i – ймовірність значення ознаки, що спостерігається, за умови, що Х иає невизначений розподіл.

В нашому випадку величина X (генеральна сукупність) розподілена нормально, тому вирівнюючі частоти знаходять за формулою:

, (5.2)

де n - кількість випробувань (обсяг вибірки);

h - довжина часткового інтервалу;

, - вибіркове середнє квадратичне відхилення;

; (5.3)

х_в. - вибіркове середнє,

х_і - середина і-го часткового інтервалу;

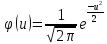(5.4)

Значення функції наведені в додатку 4.

Нормальну криву за вибірковими даними будуємо наступним чином:

1. Находимо і із застосуванням будь-якого методу:

Вибіркові дисперсії вибірок Х та Y вже знайдені методом добутків раніше. За формулою знайдемо середні квадратичні відхилення вибірок.

_(5.5)

Отримаємо:

σ_Xв = 0,96, σ_Yв = 0,77.

Використаємо обраховані раніше умовні моменти першого порядку (див. (2.2)). Знаючи їх можна легко обчислити вибіркові середні за формулою:

Отримаємо: = 0,012 = 0,031.

Обчислюємо вирівнюючі частоти для вибіркок Х та У за формулою 5.2, і заносимо у табл.№9(для вибірки Х) та у табл.№10(для вибірки У)

Таблиця №9

Таблиця №10

Полігон частот будуємо по емпіричним частотам: на координатній площині ставимо точки з координатами (x_i, n_i) (таблиця №5). Точки з’єднуємо прямими лініями.

Нормальну (теоретичну) криву будуємо по вирівнюючим частотам: на координатній площині будуємо точки з координатами (x_i, n_i).

Аналогічні дії проводимо для вибірки Y, тільки значення беремо вже з таблиці №7.

На рис. №3 зображені полігон частот і нормальна крива за вибіркою Х.

На рис. №4 зображені полігон частот і нормальна крива за вибіркою У.

Рис.3 Нормальна крива і полігон частот

для вибірки Х

Рис.4 Нормальна крива і полігон частот

для вибірки Y

Висновок: Порівнюючи графіки нормальної кривої і полігону частот можна зробити висновок, що побудована теоретична крива за даними вибірки X (мал. №3) відображають дані спостережень досить точно, а от теоретична крива за даними вибірки Y (мал.№4) відображають дані спостережень теж досить точно, але не так як . теоретична крива за даними вибірки X(ця точніше).

6. Перевірка гіпотези про нормальний розподіл генеральних сукупностей

Перевірка гіпотези про закон розподілу здійснюється за допомогою спеціально підібраної величини - критерію узгодженості.

Існує декілька критеріїв узгодженості: χ², Колмогорова, Смірнова К. Пірсона, тощо. Для перевірки гіпотези про нормальний закон розподілу генеральної сукупності скористаємось критерієм Пірсона, перевагою якого є те, що він застосовується не тільки до нормального, але і до інших розподілів. З цією метою будемо порівнювати емпіричні і теоретичні частоти, які зазвичай відрізняються.

Для того, щоб при заданому рівні значущості α перевірити нульову гіпотезу Н₀: генеральна сукупність розподілена нормально, потрібно спочатку обчислити теоретичні частоти n'_s, а потім значення критерію за даними вибірки:

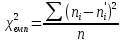(6.1)

І за таблицею критичних точок χ²(додаток 6),за даним рівним значущості α і числом ступенів вільності k=s-3 знайти критичну точку χ'_кр (α;k).

Якщо - немає підстав відхиляти нульову гіпотезу .

Якщо - нульву гіпотезу відхиляють.

Маючи теоретичні частоти, ми можемо перевірити гіпотези про нормальний розподіл генеральних сукупностей X та Y використовуючи критерій погодженості Пірсона.

Обчислимо χ²_емп для вибірки X, для чого побудуємо розрахункову таблицю № 11

Таблиця №11

ni	n'i	ni-n'i	(ni-n'i)2	((ni-n'i)2)/ni'	ni2	ni2/n'i
2	0,48	1,52	2,3104	4,81	4	8,33
5	4,6	0,4	0,16	0,03	25	5,43
11	14,48	-3,48	12,1104	0,84	121	8,36
18	15,43	2,57	6,6049	0,43	324	21,00
9	12,6	-3,6	12,96	1,03	81	6,43
3	6,34	-3,34	11,1556	1,76	9	1,42
2	0,62	1,38	1,9044	3,07	4	6,45
50	54,55			10,97		57,42

Обчислене значення критерію: .

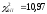Контрольна сума: .

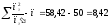Враховуючи похибки і округлення, то обчислення виконані правильно.

Тепер знайдемо χ²_кр по таблиці розподілу критичних точок χ² по рівню значущості α = 0,05 і числу степенів свободи k = 7-3 = 4 ,

χ²_кр = 9,5.,

χ2емп

11,97

Як бачимо χ²_емп > χ²_кр , отже у нас є підстави відхилити нульову гіпотезу, тобто розходження емпіричних і теоретичних частот відчутне.

Обчислимо χ²_сп для вибірки Y, для чого побудуємо розрахункову таблицю №12

Таблиця №12

ni	n'i	ni-n'i	(ni-n'i)2	((ni-n'i)2)/ni'	ni2/n'i
4	1,16	2,84	8,0656	6,95	13,79
2	4,34	-2,34	5,4756	1,26	0,92
12	9,18	2,82	7,9524	0,87	15,69
10	11,72	-1,72	2,9584	0,25	8,53
6	10,6	-4,60	21,16	2,00	3,40
12	7,4	4,60	21,16	2,86	19,46
4	3,87	0,13	0,0169	0,00	4,13
50	48,27			14,19	65,92

Обчислене значення критерію: .

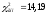Контрольна сума: .

Враховуючи похибки і округлення, то обчислення виконані правильно.

Тепер знайдемо χ²_кр по таблиці розподілу критичних точок χ² по рівню значущості α = 0,05 і числу степенів свободи k = 7-3 = 4 ,

χ²_кр = 9,5, .

Як бачимо χ²_емп > χ²_кр , отже у нас є підстави відхилити нульову гіпотезу, тобто розходження емпіричних і теоретичних частот відчутне.

Висновок: В результаті перевірки гіпотези про нормальний розподіл генеральних сукупностей X та Y за допомогою критерію погодженості Пірсона можна зробити висновок, що дані спостережень обох вибірок узгоджуються з гіпотезою про нормальний розподіл генеральних сукупностей.

7. . Перевірити гіпотезу про рівність нулю математичних сподівань генеральних сукупностей

За умовою завдання на розрахунково-графічну роботу при якісній роботі досліджуваних систем відхилення вихідного параметра від заданого значення повинне дорівнювати нулю. Тому логічно припустити, що якщо система після дії випадкових факторів повертається у нормальний стан керування, то середнє значення відхилення повинне дорівнювати нулю, інакше матиме місце систематична похибка керування, яка не залежить від дії випадкових факторів, а визначається властивостями системи.

Таким чином, якщо генеральна сукупність розподілена нормально, причому генеральне середнє а невідоме, але є підстави вважати, що воно дорівнює нулю, тобто а = 0,необхідно перевірити гіпотезу пpo рівність нулю генерального середнього. Якщо ця гіпотеза буде прийнята, то будуть підстави для висновку, що система працює без систематичних похибок керування.

Оскільки дисперсія генеральної сукупності невідома, то в якості критерію перевірки нульової гіпотези приймемо випадкову величину:

(7.1)

де S - „виправлене" середнє квадратичне відхилення;

n - обсяг вибірки;

- середнє вибіркове.

Величина Т має розподіл Стьюдента з k = n -1 ступенями вільності.

Правило перевірки нульової гіпотези формулюється так.

Правило. Для того, щоб при заданому рівні значущості а перевірити нульову гіпотезу про рівність невідомої генеральної середньої а (нормальної сукупності з невідомою дисперсією) гіпотетичному значенню

а = 0 при конкуруючій гіпотезі , потрібно обчислити спостережене значення критеріюі за таблицею критичних точок розподілу Стьюдента(додаток 7), за заданим рівнем значущості а (розміщеним у верхньому рядку таблиці розподілу Стьюдента) і числом ступенів вільності k = n -1 знайти двосторонню критичну точку t_{двост.кр.}(α,k).

Якщо |T_спост| ˂ t_{двост.кр.}- немає підстав відхилити нульову гіпотезу.

Якщо |T_спост| > t_{двост.кр.} - - нульову гіпотезу відхиляють.

Ми маємо нормально розподілену кількісну ознаку генеральної сукупності. За вибіркою n=50 знайдені в попередньому розділі вибіркове середнє :

для вибірки Х: = 0,012

для вибірки Y: = 0,031.

і “виправлене” середнє квадратичне відхилення:

для вибірки Х: 0,97

для вибірки Y: 0,77.

Перевіримо гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У при рівні значущості α = 0,05.

Обчислимо спостережене значення критерію за формулою (7.1) для вибірки Х:

Обчислимо спостережене значення критерію за формулою (7.1) для вибірки Y:

За умовою, конкуруюча гіпотеза має вигляд , тому критична область двостороння.

За таблицею критичних точок розподілу Стьюдента (додаток 7) за заданим рівнем значущості а=0,1, розміщеному у верхньому рядку таблиці, і за числом ступенів вільності k=50-1=49 знаходимо критичну точку

Оскільки |T_спост| ˂ t_{двост.кр.} - немає підстав відхилити гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У.

Висновок: Ми перевірили гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У при рівні значущості α = 0,1.

Обчисливши спостережене значення критерію для обох вибірок, ми дійшли висновку, що немає підстав відхилити гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У, оскільки