2. Знаходження оцінок математичних сподівань і дисперсійгенеральних сукупностей

Точкові оцінки невідомих параметрів розподілу можна знайти декількома методами. Один із них - метод найбільшої правдоподібності, який зводиться до знаходження максимуму функції одного або декількох аргументів (параметрів).

Вибіркова сукупність Х:

Так як ми вже знайшли певні значення в першому пункті то використаємо їх для озв’язку цього завдання. Тобто нам відома сума частот варіант інтервалів(табл.3)

Таблиця №3

частковий інтервал		сума частот n
-2,526	-1,776	2
-1,776	-1,03	5
-1,03	-0,28	11
-0,28	0,47	18
0,47	1,22	9
1,22	1,97	3
1,97	2,72	2

Створимо таблицю, що необхідна для розв’язання поставлених завдання методом добутків.

Вибираємо середини відрізків інтервалів, які і створюють послідовність рівновідалених варіант(табл.4).

Таблиця №4

xі	nі
-2,526	2
-1,486	5
-0,354	11
0,137	18
0,634	9
1,298	3
2,455	2

Вибираємо помилковий нуль. Візьмемо за нього варіанту, якій відповідає найбільша по модулю частота серед варіант, що знаходяться приблизно в середині відсортованого списку варіант. За таким принципом вибираємо С=0,137. А крок нам уже відомий, тому його шукати не будемо h=0,75. Отже знаходимо умовні варіанти:

(2.1),

Добутки частот на умовні варіанти n_iu_i, записуємо в четвертий стовпець.

Добуток частот на квадрати умовних варіант n_iu_i² запишемо в п'ятий стовпець.

Добутки частот на квадрати умовних варіант, збільшених на одиницю n_i(u_i+1)², записуємо в шостий контрольний стовпець.

Заповнюємо таблицю

Таблиця №5

x	n	u	nu	nu2	n(u+1)2
-2,526	2	-4	-7	25	13
-1,486	5	-2	-11	23	7
-0,354	11	-1	-7	5	1
0,137	18	0	0	0	18
0,634	9	1	6	4	25
1,298	3	2	5	7	19
2,455	2	3	6	19	33
	50		-8	84	117

Підраховуємо суму 2-го стопчика n_i, 4-го - n_iu_i, 5-го - n_iu_i²_, і 6-го - n_i(u_i+1)².

Тепер виконаємо контроль отриманих результатів:

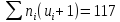
Обчислення зроблені правильно.

Обчислимо умовні моменти першого і другого порядків:

Повернемось до головного завдання - знаходження середнього вибіркового і середньої дисперсії.

(2.2)

(2.3)

Для використання даних формул нам не відомими залишається та.

Обрахуємо їх значення за формулами:

(2.4)

(2.5)

Використаємо дані формули і знайдемо невідомі нам елементи.

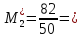
Підставимо отримані значення і знайдемо ,

=(-0,17)*0,75+0,137= 0,012

=[1,67 - (-0.17)²]*0.75²=0.925

Вибіркова сукупність Y:

Так як ми вже знайшли певні значення в першому пункті то використаємо їх для озв’язку цього завдання. Тобто нам відома сума частот варіант інтервалів(табл.6)

Таблиця №6

частковий інтервал		сума частот n
-1,618	-1,168	4
-1,168	-0,718	2
-0,718	-0,268	12
-0,268	0,182	10
0,182	0,632	6
0,632	1,082	12
1,082	1,532	4

Створимо таблицю, що необхідна для розв’язання поставлених завдання методом добутків.

Вибираємо середини відрізків інтервалів, які і створюють послідовність рівновідалених варіант(табл.7).

Таблиця №7

yi	ni
-1,618	4
-1,055	2
-0,511	12
0,007	10
0,378	6
0,769	12
1,179	4

Вибираємо помилковий нуль. Візьмемо за нього варіанту, якій відповідає найбільша по модулю частота серед варіант, що знаходяться приблизно в середині відсортованого списку варіант. За таким принципом вибираємо

С= 0,769.

. А крок нам уже відомий, тому його шукати не будемо h=0,45. Отже знаходимо умовні варіанти за формулою(2.1), тільки замість х підставляємо у.

Добутки частот на умовні варіанти n_iv_i, записуємо в четвертий стовпець.

Добуток частот на квадрати умовних варіант n_iv_i² запишемо в п'ятий стовпець.

Добутки частот на квадрати умовних варіант, збільшених на одиницю n_i(v_i+1)², записуємо в шостий контрольний стовпець.

Заповнюємо таблицю

Таблиця №8

yi	ni	vi	nivi	nivi2	ni(vi+1)2
-1,618	4	-5	-21	113	74
-1,055	2	-4	-8	33	19
-0,511	12	-3	-34	97	41
0,007	10	-2	-17	29	5
0,378	6	-1	-5	5	0
0,769	12	0	0	0	12
1,179	4	1	4	3	15
	50		-82	279	165

Підраховуємо суму 2-го стопчика n_i, 4-го - n_iv_i, 5-го - n_iv_i²_, і 6-го - n_i(v_i+1)².

Тепер виконаємо контроль отриманих результатів:

Обчислення зроблені правильно.

Обчислимо умовні моменти першого і другого порядків:

Повернемось до головного завдання - знаходження середнього вибіркового і середньої дисперсії.

Обчислюємо умовні моменти першого і другого порядків за формулами (2.4), (2.5):

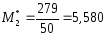
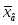
Підставимо отримані значення і знайдемо , за формулами (2.2), (2.3):

=(-1,639)*0,45+0,769= 0,031

=[5,580 - ()²]*0.45²=0.586.