2.4. Симетричні рівняння і обернені рівняння

Приклади:

1.

2.

3.

4.

5.

Означення: алгебраїчне рівняння n-го степеня називається

симетричним, якщо у нього рівні коефіцієнти при і , тобто воно має вигляд:

де. Безпосередньою перевіркою переконуємося, щоє коренем симетричного рівняння непарного степеня. Поділивши симетричне рівняння непарного степеня нами отримаємо симетричне рівняння парного степеня. Симетричні рівняння парного степеня підстановкоюзводяться до рівнянь у два рази меншого порядку.

Приклади:

1)

Дане рівняння має корінь так як це симетричне рівняння непарного степеня . Розклавши ліву частину на множники отримаємо:

Розв’яжемо рівняння

Поділимо обидві частини цього рівняння на (так як не є коренем), отримаємо:

або.

Після заміни отримаємо рівняннякоренями якого є числаі. Таким чином, ми отримали сукупність рівнянь:

або

Розв’язуючи ці рівняння, знаходимо корені:

Відповідь: 1,.

2) .

Оскільки  не є коренем рівняння, поділимо обидві частини рівняння на , отримаємо

,

,

виносимо за дужки спільний множник 

,

робимо заміну змінної ; підносимо обидві частини отриманої рівності в квадрат , виражаємо 

підставляємо отриманий вираз в рівняння і розв'язуємо рівняння ; ; ;  або . Повертаємося до заміни і розв'язуємо рівняння

а) ;  ; .

б) ;  ; ; ; ; .

Відповідь: ; ; .

3) .

Оскільки  не є коренем рівняння, поділимо обидві частини рівняння на , отримаємо

,

,

виносимо за дужки спільний множник 

,

робимо заміну змінної ; підносимо обидві частини отриманої рівності в квадрат, виражаємо,

підставляємо отриманий вираз в рівняння і розв'язуємо рівняння ,або. Повертаємося до заміни і розв'язуємо рівняння

а) ;.

б) ;;дійсних розв’язків немає.

Відповідь: .

4).

Оскільки  не є коренем рівняння, поділимо обидві частини рівняння на , отримаємо

,

,

виносимо за дужки спільний множник 

,

робимо заміну змінної ; підносимо обидві частини отриманої рівності в квадрат, виражаємо,

підставляємо отриманий вираз в рівняння і розв'язуємо рівняння ,або. Повертаємося до заміни і розв'язуємо рівняння

а) ;.

б) ;

Відповідь: ,

5) .

Ділимо на , отримуємо

,

,

виносимо за дужки спільний множник 

,

робимо заміну змінної ; підносимо обидві частини отриманої рівності в квадрат, виражаємо,

підставляємо отриманий вираз в рівняння і розв'язуємо рівняння ,або. Повертаємося до заміни і розв'язуємо рівняння

а) ,не має дійсних розв’язків.

б) ;.

Відповідь:  .

2.5. Дробово-раціональні рівняння

Рівняння типу розв’язуються з використанням заміни або (частіше).

Приклади:

1.

2.

3.

4.

5.

1) ОДЗ:.

Зробимо заміну ; піднесемо обидві частини до квадрату, отримаємо , виразимо  і підставимо в вихідне рівняння, отримаємо . Розв'язуємо отримане рівняння ; ;  ;  отримуємо два рівняння:

а) ; ; ; .

б) ; ; , .

Відповідь: ; ; .

2)

Проведемо певну підготовчу роботу з даним рівнянням, а саме – розділимо чисельник та знаменник лівої частини рівняння на (це зробити можна, так як 0 не є коренем цього рівняння).

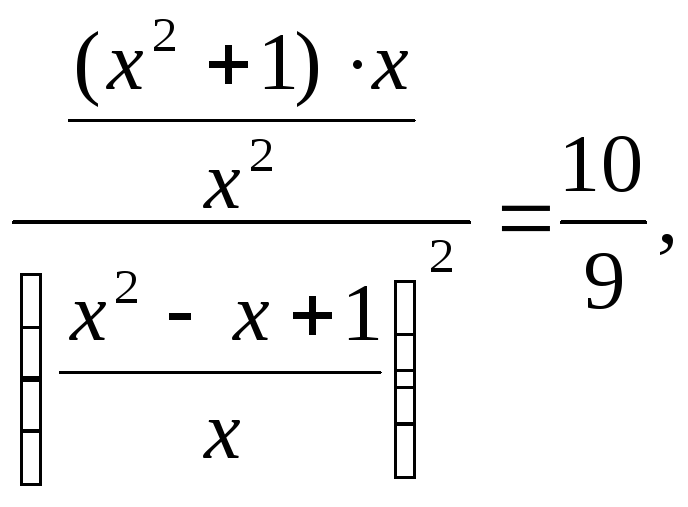або

Ввівши підстановку, отримаємо:

Звідки Провівши обернену заміну, отримаємо сукупність рівнянь, що рівносильна вихідному рівнянню:

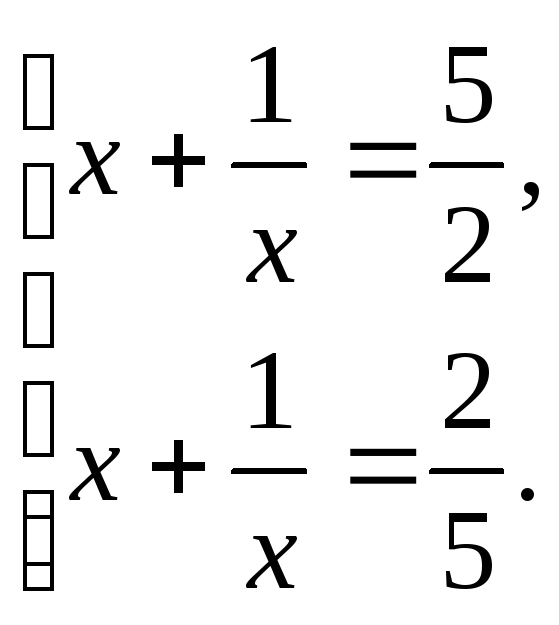
З першого рівняння отримаємо два розв’язки а друге рівняння дійсних коренів не має. Отже, знайдені розв’язки першого рівняння сукупності і будуть розв’язками вихідного рівняння у множині дійсних чисел.

3)

У лівій частині рівняння стоїть сума двох квадратів. Спробуємо доповнити її до квадрата різниці. Отримаємо:

або,

або

Використаємо підстановку . Отримаємо рівнянняяке має кореніПерейшовши до змінної, маємо:

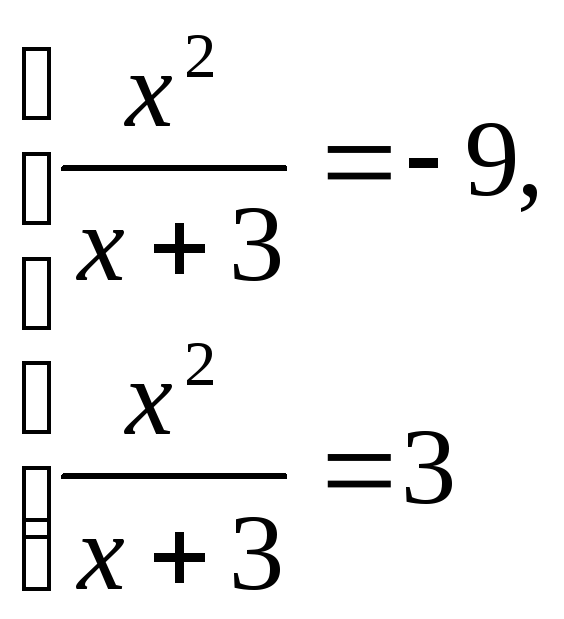
Перше рівняння сукупності у множині дійсних чисел розв’язків не має, а з другого рівняння отримаємо розв’язки вихідного рівняння:

Відповідь:

4) .

Зробимо підстановку , піднесемо обидві частини до квадрату, отримаємо, виразимоі підставимо у вихідне рівняння, отримаємоРозв'язуємо отримане рівняння,отримуємо два рівняння:

а) ;;;.

б) ;дійсних розв'язків немає.

Відповідь: ,.

5) .

Вводимо підстановку , піднесемо обидві частини до кубу, отримаємо, виразимоі підставимо у вихідне рівняння, отримаємоРозв’язуємо отримане рівнянняабо, отримуємо три рівняння.

При дійсних розв’язків немає.

а) ,

б) ,

Відповідь: