StrMech-КРАТКО_2011_часть_2

Оглавление

6 Определение перемещений в стержневых системах . . . . . 3

6.1 Вводные замечания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 6.2 Общая формула для определения перемещений

в плоских стержневых системах. . . . . . . . . . . . . . . . . . . . . 4 6.3 Формула Мора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 6.4 Техника вычисления интегралов Мора . . . . . . . . . . . . . . . 10

7 Метод сил и его применение к расчету плоских рам и балок . . . 13

7.1 Статически неопределимые системы и их свойства . . . . . . . 13 7.2 Основная система и основные неизвестные метода сил . . . . 18 7.3 Канонические уравнения метода сил . . . . . . . . . . . . . . . . 20 7.4 Вычисление и проверка коэффициентов и свободных

членов канонических уравнений . . . . . . . . . . . . . . . . . . . 22 7.5 Определение внутренних усилий в заданной

статически неопределимой системе . . . . . . . . . . . . . . . . . . 24 7.6 Проверка правильности определения внутренних усилий.

Алгоритм расчета рам методом сил . . . . . . . . . . . . . . . . . . 26

8 Применение метода сил к расчету статически неопределимых арок, ферм и неразрезных балок . . . . . . . 29

8.1Статически неопределимые арки и методы их расчета . . . . 29

8.2Расчет двухшарнирной арки на неподвижную нагрузку . . . 31

8.3 Расчет двухшарнирной арки с затяжкой . . . . . . . . . . . . . . 33 8.4 Расчет бесшарнирной арки на неподвижную нагрузку . . . . 34 8.5 Расчет статически неопределимых ферм . . . . . . . . . . . . . . 36 8.6 Расчет неразрезных балок. Основная система метода сил . . 39 8.7 Уравнение трех моментов . . . . . . . . . . . . . . . . . . . . . . . . 42

9 Метод перемещений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

9.1 Кинематическая неопределимость . . . . . . . . . . . . . . . . . . . 46 9.2 Основная система метода перемещений . . . . . . . . . . . . . . . 49 9.3 Канонические уравнения метода перемещений . . . . . . . . . . 51 9.4 Вычисление и проверка коэффициентов и свободных

членов канонических уравнений . . . . . . . . . . . . . . . . . . . 52 9.5 Определение внутренних усилий и их проверка.

Алгоритм расчета рам методом перемещений . . . . . . . . . . . 55

10 Смешанный метод расчета статически неопределимых систем 58

10.1 Выбор метода расчета статически неопределимой системы 58 10.2 Смешанный метод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

Список литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 Приложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

6Определение перемещений в стержневых системах

6.1Вводные замечания

6.1.1Цель определения перемещений. Перемещением данной точки сооружения называется изменение ее координаты, вызванное деформацией системы. Перемещения могут быть линейными

(например, прогибы, удлинения элементов) и угловыми (углы поворота, углы закручивания сечений).

Инженерные сооружения должны проектироваться не только прочными, но и достаточно жесткими, т. е. перемещения различ- ных точек конструкций должны быть достаточно малыми.

Чтобы контролировать сооружения после постройки и длительной эксплуатации и не допускать возникновения предельных состояний, периодически измеряют характерные перемещения точек конструкций и сравнивают с расчетными значениями.

Задача нахождения перемещений возникает не только при оценке жесткости сооружения. При определении внутренних усилий в статически неопределимых системах, а также в задачах динамики сооружений перемещения вычисляют на промежуточ- ном этапе расчета.

Наиболее общим и универсальным методом вычисления перемещений в стержневых системах является метод Мора. Он позволяет находить любые типы перемещений (удлинения стержней, прогибы, углы поворота, и т. п.) от произвольных нагрузок и воздействий (например, температурных или кинематических).

6.1.2 Особенности применения принципа возможных перемещений к деформируемым системам. Напомним, как с помощью указанного принципа находятся усилия в статически определимых системах. Система превращается в механизм отбрасыванием той связи, реакция в которой определяется; механизму задаются возможные перемещения; составляется уравнение возможных работ, из которого выражается искомое усилие. При этом деформации элементов не учитываются, поэтому возможная работа внутренних сил равна нулю: A(i) = 0 . Однако по этой методике можно определять не только опорные реакции, но и внутренние силы: их предварительно необходимо перевести в разряд внешних, представив как реакции в одиночных стерженьках, скрепляющих две части конструкции.

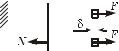
При определении перемещений деформации системы учитывать необходимо (т. е. вести расчет по деформированной схеме). Принцип возможных перемещений Лагранжа в этом слу- чае формально записывается в виде:

A(e) + A(i) = 0 ,

ãäå A(e) – возможная работа внешних сил; A(i) – возможная работа внутренних сил.

Рассмотрим, в чем заключаются особенности применения принципа возможных перемещений к деформируемым системам.

1) При положительных направлениях внутренних сил, соответствующих положительным деформациям, работа внутренних сил отрицательна, так как направления внутренних сил и деформаций, вызванных внешними силами, противоположны.

малых возможных перемещений, можно распространить и на малые конечные перемещения, удовлетворяющие связям.

6.2Общая формула для определения перемещений

вплоских стержневых системах

6.2.1 Плоские системы, состоящие из прямолинейных стержней. Рассмотрим систему, состоящую из прямолинейных стержней (рисунок 6.2, à). Обозначим через S длину оси системы, s – координату, отсчитываемую вдоль оси.

Пусть по какой-либо причине система деформировалась, в результате чего ее точки получили малые перемещения. Произвольный бесконечно малый элемент системы длиной ds с координатой s испытывает деформации удлинения, сдвига и изгиба. Его левое сечение условно будем считать неподвижным.

Обозначим: s – удлинение элемента, y – полный сдвиг се- чений, θ – угол поворота сечений при изгибе (рисунок 6.2, á).

Допустим, требуется определить вертикальное перемещение ∆ точки K. Для этого сформируем вспомогательное «единичное» состояние той же системы: по нàправлению искомого перемещения приложим единичную силу P = 1 (рисунок 6.2, â) и определим

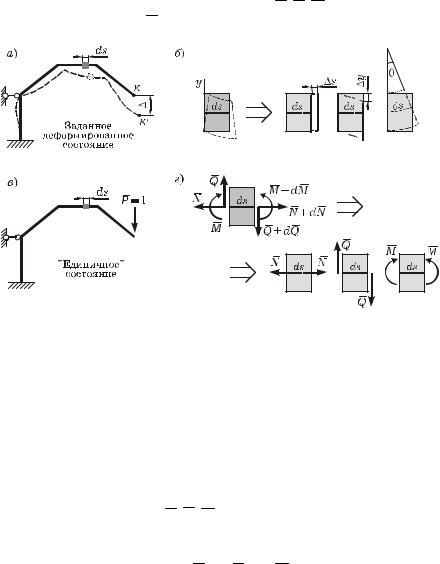
возникающие от нåå внутрåнние усилия N, Q, M (рисунок 6.2, ã). Приращениями dN, dQ, dM будем пренебрегать.

Рисунок 6.2

«Единичное» состояние является состоянием равновесия. Тогда, согласно принципу возможных перемещений, сумма возможных работ сил этого состояния на любых возможных перемещениях должна быть равна нулю. В качестве возможных примем перемещения заданного деформированного состояния, указанные на рисунке 6.2, à, á. Они хотя и конечны, но весьма малы по сравнению с размерàìи элементов и удовлетворяют связям.

Внешняя сила P = 1 «единичного» состояния совершает на перемещении ∆ заданного деформированного состояния возможную работу

Внутренние усилия N, Q, M «единичного» состояния совершают на элементарных перемещениях ∆s, ∆y, θ заданного состояния элементарную возможную работу

dA(i) = −(N s + Q y + Mθ).

Элементарная работа dA(i) может рассматриваться как сумма независимых работ продольной силы, поперечной силы и изгибающего момента на соответствующих перемещениях за счет растяжения, сдвига и изгиба элемента ds.

Просуммируем работы внутренних сил для всех элементов системы, т. е. проинтегрируем выражение элементарной работы dA(i) по длине оси системы S. В результате получим возможную работу внутренних сил «единичного» состояния на перемещениях заданного деформированного состояния для всей системы:

величину ds.

Формула (6.3) позволяет найти любые перемещения в любой плоской системе, состоÿщей из прямолинейных стержней. Вспо-

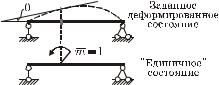
Чтобы определить, например, угол поворота θ какого-либо узла или сечения (рисунок 6.3), то вспомогательную нагрузку нужно принять в виде внешнего

момента m =1, приложенного в этом узле (или к этому сечению). Тогда возможная работа внешних сил бу-

гичен расчету при вычислении .

6.2.2Замечания. 1) При использовании формулы (6.3) несущественно, от чего возникли деформации элементов системы. Они могли быть вызваны нагрузкой, изменением температуры, ползу- честью материала и т. п. Важно лишь то, что деформации должны быть известны. Отметим, что стержневая система может быть как статически определимой (не содержать лишних связей), так и статически неопределимой.

2) Формулу (6.3) допустимо использовать для стержней малой кривизны.

6.3Формула Мора

6.3.1Вывод формулы Мора. Практически наиболее важна задача определения перемещений от заданной неподвижной нагруз-

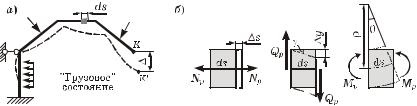
ки. В этом случае заданное деформированное состояние конструкции называют «грузовым» (рисунок 6.4, à).

Рисунок 6.4

Взаимные перемещения сечений элемента ds в «грузовом» состоянии (рисунок 6.4, á) выражаются через внутренние усилия этого состояния Np , Qp , Mp и жесткости EA, GA è EJ. Здесь E – модуль Юнга, G – модуль сдвига, A – площадь сечения, J – момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгиба.

Для линейно деформируемой системы можно воспользоваться формулами сопротивления материалов, согласно которым

Коэффициент η зависит только от формы сечения. Например, для круга η = 32/27; для прямоугольника η = 1,2; для прокатных двутавров η ≈ A/Aw, ãäå A – полная площадь сечения двутавра; Aw – площадь вертикальной стенки.

Подставив выражения (6.4) в формулу (6.3) и представив интеграл в виде суммы трех интегралов, получим

EA, GA, EJ – жесткости поперечного сечения при растяжении– сжатии, сдвиге и изгибе; η – коэффициент, учитывающий неравномерность распределения касательных напряжений при изгибе по сечению.

Соотношение (6.5) называют формулой Мора èëè интегралом Мора для плоской стержневой системы.

Таким образом, формула Мора (6.5) позволяет по известным эпюрам внутренних усилий от заданной нагрузки и единичного

воздействия определить перемещение любого вида. Геометриче- ская задача (вычисление перемещений по деформациям элементов системы) сводится к статической задаче (определение усилий от заданного и единичного воздействия).

6.3.2 Порядок определения перемещений с помощью формулы Мора. Чтобы определить перемещение по заданному направлению, необходимо:

найти внутренние усилия на отдельных участках системы от заданной нагрузки (в «грузовом» состоянии);

по направлению искомого перемещения приложить единич- ное усилие (для линейных перемещений – сосредоточенную силу, для угловых – момент) и найти внутренние усилия в полученном «единичном» состоянии;

подставив найденные выражения усилий в формулу Мора, определить искомое перемещение интегрированием по отдельным участкам системы и суммированием результатов.

Границами участков системы, как правило, служат точки приложения сосредоточенных сил и моментов или изломы оси (в рамах). Участками являются также отдельные стержни фермы.

Если найденное перемещение положительно, то его направление совпадает с направлением приложенной единичной силы, если отрицательно – противоположно ему.

6.3.3 Частные случаи применения формулы Мора. Влияние каждого из слагаемых в формуле (6.5) на результат неодинаково. Для многих конструкций «вклад» некоторых внутренних усилий не превышает 1–3 %, поэтому в инженерных расчетах их допускается не учитывать.

Балки, испытывающие плоский изгиб. В сечениях балок возникают поперечные силы и изгибающие моменты, продольные силы отсутствуют. Обозначим: l – длина балки, h – высота поперечного сечения. Если l/h > 8, то в формуле Мора допускается учитывать только изгибающие моменты:

Åñëè 5 ≤ l/h ≤ 8, то необходимо учесть еще и поперечные силы:

Åñëè l/h < 5, то конструкция не является стержневой системой, и формула Мора дает большие погрешности в расчетах, поэтому перемещения следует определять методами теории упругости.

Арки и криволинейные стержни. Как правило, строительные арки являются пологими с отношением ρ/h > 10 (ρ – радиус кривизны оси арки, h – высота поперечного сечения). Для них с достаточной степенью точности можно пользоваться формулой Мора (6.5), полученной для прямолинейных элементов.

Влияние поперечных и продольных сил на перемещения в арках, как правило, больше, чем в рамах. Оно может быть оценено только по результатам расчета. При прочих равных условиях влияние N è Q для бесшарнирных арок обычно больше, чем для двухшарнирных. Поскольку арка во многих случаях представляет собой основную часть дорогого и ответственного сооружения, то не следует игнорировать влияние отдельных внутренних сил при определении перемещений.

Допускается пренебрегать влиянием поперечных сил на перемещения, учитывая только изгибающие моменты и продольные силы:

= S∫MEJpM ds + S∫NEApN ds .

Следует отметить, что сравнительное влияние продольных сил в арках зависит не только от размеров арки, но и от нагрузки.

Фермы. Для идеальных шарнирных ферм отличны от нуля только продольные силы в стержнях, которые, как и жесткости, постоянны по длине каждого отдельного стержня. Формула Мора принимает вид:

= S∫NEApN ds .

Вдоль каждого i-го стержня фермы введем свою ось zi. Интеграл по длине оси системы заменим суммой интегралов по длине каждого i-го стержня. Постоянные силы и жесткости вынесем за знак каждого интеграла; интеграл от dzi даст длину li:

ãäå Np(i) , N(i) – продольная сила в i-ом стержне соответственно в «грузовом» и «единичном» состояниях; li, EAi – длина и жесткость i-го стержня; zi – координата, отсчитываемая вдоль оси i-го стержня. Знак суммы распространяется на все стержни фермы.

6.4 Техника вычисления интегралов Мора

Основным недостатком определения перемещений по формуле Мора является необходимость составления аналитических выражений подынтегральных функций. Это особенно сложно при большом количестве участков системы.

Во многих случаях интегралы Мора удобно искать не через первообразные функции, а численными способами с использованием эпюр внутренних усилий. В связи с этим подобные способы называют способами «перемножения эпюр». Применимы они к любому из трех интегралов формулы Мора.

6.4.1 Способ (правило) Верещагина. Рассмотрим прямолинейный участок длиной l (рисунок 6.6). Интеграл от произведения двух функций f1(z) f2 (z) (при условии, что вторая функция линейная) равен