StrMech-КРАТКО_2011_часть_2

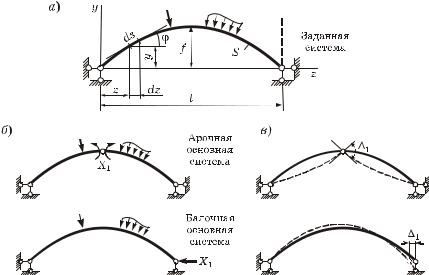
8.2 Расчет двухшарнирной арки на неподвижную нагрузку

Заданная двухшарнирная арка (рисунок 8.3, à) содержит одну лишнюю связь, поэтому для получения статически определимой основной системы метода сил необходимо эту связь отбросить и заменить действием реакции X1.

Основная система метода сил может быть образована двумя способами (рисунок 8.3, á): в виде трехшарнирной арки (арочная основная система) или криволинейной балки (балочная основная система). В первом случае X1 представляет собой изгибающий момент в замковом сечении, во втором – горизонтальную опорную реакцию (распор).

Условием эквивалентности основной и заданной систем явля-

ãäå δ11 – перемещение по направлению X1, вызванное единичным силовым фактором, приложенным в направлении X1; 1p – перемещение по направлению X1 от внешней нагрузки.

Рисунок 8.3

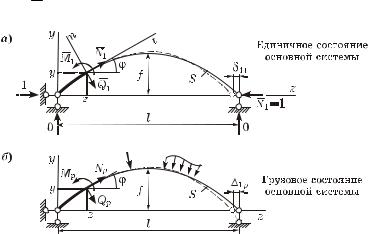
Далее следует сформировать единичное и грузовое состояния основнîé ñèñòåмы, определить в каждом из них внутренние усилия – M1, Q1, N1 è Mp, Qp, Np соответственно (рисунок 8.4).

Рисунок 8.4

Затем, воспользовавшись методом Мора, необходимо найти перемещения δ11 è 1p:

ãäå S – длина оси арки; ds – бесконечно малый элемент оси; EJ, GA, EA – жесткости сечения соответственно при изгибе, сдвиге и растяжении-сжатии; η – коэффициент, учитывающий неравномерность распределения касательных напряжений по поперечному сечению при изгибе и зависящий от формы сечения.

Из уравнения (8.1) следует, что

Теперь, зная X1, по принципу суперпозиции можно определить изгибающие моменты, поперечные и продольные силы в заданной арке:

Для контроля вычисленных внутренних усилий выполняется кинематическая (деформационная) проверка. Для этого определяется перемещение

h < l /10 допускается не учитывать поперечные силы при определении δ11 по формуле (8.8), продольные и поперечные силы – при определении 1ð по формуле (8.9). При этом погрешность по сравнению с точным расчетом не превысит 1–2 %. Однако если ось арки при заданной схеме нагружения близка к рациональной оси аналогичной трехшарнирной системы, необходимо учитывать все силовые факторы (M, Q, N).

8.3 Расчет двухшарнирной арки с затяжкой

Затяжка воспринимает распор арки и работает на растяжение. Общий ход расчета практически не отличается от рассмотренного выше.

Рассмотрим арку с затяжкой выше уровня опор, воспринимающую вертикальную нагрузку (рисунок 8.5, à). Основная система получается разрезанием затяжки и введением в ней неизвестной продольной силы Õ1 (рисунок 8.5, á).

Рисунок 8.5

В процессе деформирования системы затяжка удлиняется на

lç = X1lç , EçAç

ãäå lç – длина затяжки; ÅçÀç – ее жесткость (Åç – модуль Юнга, Aç – площадь сечения).

Уравнение для определения Õ1 получим из условия

Знак минус в правой части потому, что направления данного перемещения и силы X1 противоположны.

По принципу суперпозиции

ãäå δ11 è 1p – перемещения в направлении Õ1 от действия единичной силы в этом же направлении и от внешней нагрузки соответственно.

Приравнивая правые части соотношений (8.6) и (8.7) и приводя подобные, получаем каноническое уравнение:

Перемещения δ11 è 1p в основной системе определяются по формулам (8.2).

Дальнейший расчет ведется по методике, изложенной в п. 8.2 для двухшарнирной арки без затяжки. Из уравнения (8.8) с уче- том (8.9) определяется

Далее по зависимостям (8.4) находятся изгибающие моменты, поперечные и продольные силы и выполняется кинематическая (деформационная) проверка по формуле (8.5). В отличие от арки без затяжки, 1 должно получиться, согласно (8.6), равным

−X1lç /(EçAç ) .

8.4 Расчет бесшарнирной арки на неподвижную нагрузку

Бесшарнирная арка (рисунок 8. 6, à) три раза статически неопределима ( nc = 3 ). Основная система метода сил получается удалением трех избыточных связей, например, введением трех шарниров (рисунок 8.6, á), отбрасыванием жесткой опоры (рисунок 8.6, â); разрезанием арки по оси симметрии (рисунок 8.6, ã) и добавлением неизвестных реакций этих связей X1, X2, X3 .

Для симметричной арки желательно выбирать и симметрич- ную основную систему. В этом случае многие расчеты можно будет производить только для половины арки.

Канонические уравнения выражают условия отсутствия перемещений по направлениям неизвестных усилий X1, X2, X3. В первом случае это углы поворота опорных сечений и взаимный угол поворота сечений в замке; во втором – линейные и угловое пере-

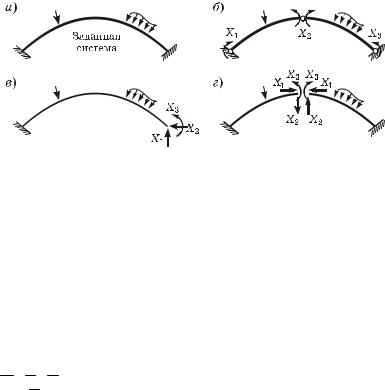
мещения конца консоли. Для основной системы на рисунке 8.6, ã канонические уравнения (8.18) выражают условие полной взаимной неподвижности левого и правого сечений в месте разреза.

Рисунок 8.6

В общем случае канонические уравнения имеют вид:

Входящие в них перемещения определяются по методу Мора:

ãäå Mi , Qi , Ni è Mp, Qp, Np – внутренние усилия в основной системе от Xi = 1 и внешней нагрузки соответственно; S – длина оси арки; ds – бесконечно малый элемент оси; EJ, GA, EA – жесткости сечения соответственно при изгибе, сдвиге и растяжениисжатии; η – коэффициент, учитывающий неравномерность распределения касательных напряжений по поперечному сечению при изгибе и зависящий от формы сечения.

Наиболее простой расчет получится с использованием основной системы, показанной на рисунке 8.6, ã, так как четыре из побочных коэффициентов будут нулевыми:

δ12 = δ21 = δ23 = δ32 = 0 .

После решения канонических уравнений вычисляются значе- ния внутренних усилий M, N, Q по формулам:

M= M1X1 +M2X2 +M3 X3 +Mp ;

N= N1X1 +N2X2 +N3 X3 +Np ;

Q = Q1X1 +Q2X2 +Q3 X3 +Qp .

Далее необходимо выполнить кинематическую (деформационную) проверку правильности вычисления внутренних усилий. Для этогî ìîæíî использовать усилия одного из единичных состояний Mi , Qi , Ni (i = 1, 2, 3)

вий (8.13) и (8.14) говорит о том, что перемещения по направлениям реакций отброшенных связей отсутствуют, что соответствует расчетной схеме заданной бесшарнирной арки.

8.5Расчет статически неопределимых ферм

8.5.1Статическая неопределимость плоских ферм. Применяемые на практике фермы, строго говоря, никогда не бывают статически определимыми, так как не имеют идеальных шарнирных соединений в узлах. Однако здесь будем рассматривать статиче- скую неопределимость, обусловленную наличием избыточных стержней в шарнирно-стержневых расчетных схемах, а не жесткостью узлов.

Степень статической неопределимости (количество лишних

стержней) определяется по формуле (7.3):

ãäå Ó – количество узлов фермы (шарниров), непосредственно не связанных с землей; ÑÎ – количество одиночных связей (стержней фермы и опорных стержней).

Избыточными (лишними) могут быть как связи опор, так и элементы самой фермы. Внешне статически неопределимая

ферма содержит лишние опорные стержни, но сама она, отделенная от опор, статически определима. Внутренне статически неопределимая ферма имеет минимально необходимое количество

опорных связей, однако в ее структуре присутствуют больше стержней, чем нужно для неизменяемости (рисунок 8.7).

Рисунок 8.7

Заметим, что такое разделение ферм является условным. Например, систему на рисунке 8.8, à можно трактовать или как внутренне, или как внешне статически неопределимую. Лишним здесь можно считать элемент самой фермы либо опорный стержень: отбросив его, получим статически определимую систему (рисунок 8.8, á).

Рисунок 8.8

Как и всякая статически неопределимая система, ферма может иметь начальные усилия, обусловленные неточностью сборки или нивелировки опор, а также температурой. Однако с конструктивной точки зрения статически определимые фермы сложнее, так как приходится устраивать шарниры, подвижные опоры, разрезать систему при помощи специальных швов. В тоже время статически неопределимые фермы в целом более надежны, так как аварии отдельных ее элементов не приводят к столь тяжелым последствиям, как разрушение элементов статически определимых ферм.

8.5.2 Общий ход расчета. Основная система метода сил образуется разрезанием стержней фермы либо устранением избыточных опорных связей. Например, для трижды статически неопределимой фермы на рисунке 8.9 показано несколько ее вариантов.

Заметим, что основная система, получаемая разрезанием стержней фермы, во многих случаях оказывается удобнее основной системы, в которой устраняются опорные связи. Например, первый вариант основной системы на рисунке 8.9 удобнее второго и третьего, потому что в нем продольные силы от внешней на-

ãäå N(j) – продольная сила в j-ом стержне заданной фермы.

Далее следует выполнить статическую проверку правильности вычисления внутренних усилий, вырезав несколько узлов и проверив их равновесие.

Äëÿ кинематической (деформационной) проверки необходимо взять усилия одного из единичных состояний (k = 1, 2, …, n)

вий (8.18) и (8.19) говорит о том, что перемещения по направлениям усилий в разрезанных стержнях равны удлинениям этих стержней, что соответствует расчетной схеме заданной фермы.

8.6Расчет неразрезных балок. Основная система метода сил

8.6.1Общие сведения о неразрезных балках. Неразрезной называется статически неопределимая сплошная балка, имеющая более двух опор и, следовательно, перекрывающая более одного пролета (рисунок 8.10, à).

Рисунок 8.10

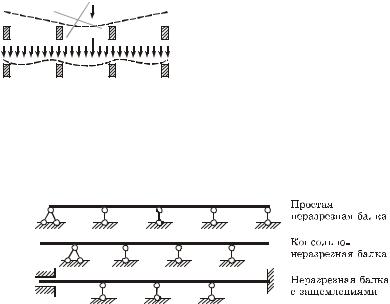
Характерным ее отличием от многопролетной шарнирной балки (рисунок 8.10, á) является то, что нагрузка, приложенная в любом пролете, изгибает неразрезную балку на протяжении всех ее пролетов, создавая плавную упругую линию.

Закрепление концов балки производится так, чтобы равномерный нагрев (охлаждение) не вызывало появление дополнительных усилий. На расчетной схеме одна из крайних опор может быть шарнирно неподвижной или жесткой заделкой, а вторая должна быть шарнирно подвижной или скользящей заделкой (см. рисунок 8.10). Все промежуточные опоры рассматриваются как шарнирно подвижные.

Действительная конструкция прикрепления неразрезной балки к опорам обычно отступает от указанной выше схемы. На прак-

Можно выделить следующие типы неразрезных балок: простая неразрезная – если балка своими концами опирается на шарнирные опоры; консольно-неразрезная – если имеет консоли;

неразрезная балка с защемлениями – если ее концы закреплены жесткой и скользящей заделками (рисунок 8.12).

Рисунок 8.12

8.6.3 Основная система метода сил. Рассмотрим простую неразрезную балку, имеющую на концах шарнирные опоры. Условимся нумеровать опоры слева направо так, чтобы для каждого пролета номер правой опоры совпадал с номером пролета, а левой – был на единицу меньше (рисунок 8.13, à). Начинать будем, как правило, с 0.

Основную систему можно получить: