
StrMech-КРАТКО_2011_часть_2
.pdf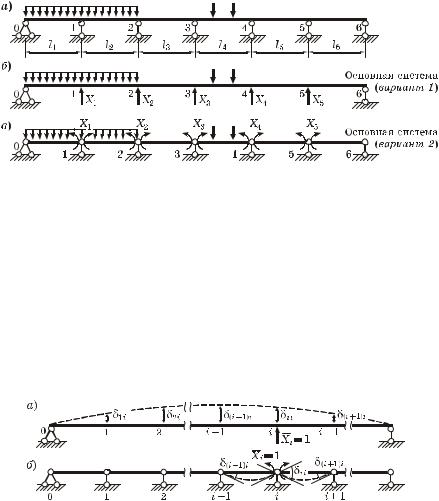
1)устраняя все промежуточные опоры и принимая в качестве неизвестных вертикальные опорные реакции (рисунок 8.13, á);
2)вводя шарниры, чаще всего в сечения над промежуточными опорами, и принимая за неизвестные опорные изгибающие моменты (рисунок 8.13, â).
Рисунок 8.13
Нетрудно убедèться, что для первого варианта основной системе любая сила Xi = 1 вызывает перемещения по направлениям всех неизвестных сил (рисунок 8.14, à). Для второго варианта основной системы любой момент Xi = 1 деформирует только два смежных пролета по обе стороны от опоры, где он приложен, и вызывает перемещения только по направлениям трех неизвестных: Õi–1 , Õi è Õi+1 (рисунок 8.14, á).
Следовательно, в |
первой основной системе каждое побоч- |
ное перемещение δij |
(i ≠ j) не равно нулю, и канонические урав- |
нения будут полными. Во второй основной системе большое число |
|
побочных коэффициентов будет равно нулю, канонические уравнения упростятся. Следовательно, вторая основная система рациональнее первой, она и будет рассматриваться далее.
Рисунок 8.14
Заметим, что при малом числе промежуточных опор (1–2) может применяться и первый вариант основной системы.
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
41 |

8.7Уравнение трех моментов
8.7.1Вывод уравнения трех моментов. Положим, что балка имеет ступенчато переменное сечение с постоянным моментом
инерции Ji в каждом i-м пролете.
Рассмотрим два смежных пролета выбранного варианта основной системы, i-é è (i + 1)-й (рисунок 8.15, à). Запишем i-ое каноническое уравнение метода сил:
δi1X1 + δi2 X2 + . . . + δi(i −1) Xi −1 + δii Xi + δi(i +1) Xi +1 + . . . + |
|
+ δin Xn + ip = 0 . |
(8.20) |
Рисунок 8.15
42 |
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
Очевидно, что моменты X1, X2 , . . ., Xi −2 è Xi +2 , . . ., Xn не деформируют рассматриваемые пролеты балки и, следовательно, не
вызывают перемещений по направлению момента Xi . Поэтому |
||
коэффициенты δi1 = 0; δi2 = 0; . . .; δi(i −2) = 0; |
δi(i +2) = 0; |
. . .; δin = 0 . |
Óравнение (8.20) принимает вид: |
|
|
δi(i −1) Xi −1 + δii Xi + δi(i +1) Xi +1 + |
ip = 0 . |
(8.21) |
Коэффициенты и свободный член этого уравнения представля- þт собой óãëû ïîâорота сечений балки над i-й опорой, вызванные Xi −1 = 1, Xi = 1, Xi +1 = 1 и внешней нагрузкой соответственно.
При определении перемещений по методу Мора будем учитывать только изгибающие моменты, пренебрегая поперечными силами. Эпюры, необходимые для вычисления единичных перемещений δi(i −1) , δii , δi(i +1) , входящих в уравнение (8.21), построены на рисунке 8.15, á–ã. Перемножая их по правилу для прямолинейных эпюр на участке постоянной жесткости, получаем:
|
|
|
|
|
|
|
δi(i −1) |
= |
∫ |
|
M |
i |
M |
i −1 |
ds = |
|
li |
|
|
|
|
1 |
1 |
= |
li |
|
|
|
; |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
EJ |
|
6EJ |
i |
6EJ |
i |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
( |
|
|
i )2 ds = |
|
|
li |
|
|
|
|
|
|
|
|
|
|
li +1 |
|
|
|
|
|
|
|
|
|
|
li |
|
|
|
|
li +1 |
|
|
|||||||||||||
δii |
= |
∫ |
M |
|
|
|
|
|
2 |
1 |
1 + |
|
|
|
|
|
2 |
1 1 = |
|
|
|
|
+ |
|
|
; |
||||||||||||||||||||||||||
|
|
|
6EJ |
|
6EJ |
|
|
|
|
|
3EJ |
|
3EJ |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
EJ |
|
|
i |
|
|
|
|
|
|
|
|
i +1 |
|
|
|
|
|
i |
|
i |
+1 |
|
||||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
δi(i +1) |
= ∫ |
M |
i |
M |
i +1 |
ds |
= |
|
|
li =1 |
|
|
1 |
1 = |
|
|
li +1 |
. |
|
|
|
|
(8.22) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
EJ |
|
|
|
|
6EJi =1 |
|
|
6EJi +1 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Подставим соотношения (8.22) в уравнение (8.21): |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
li |
|
|
|
|
|
|
li |
|
|
|
|
|
|
|
|
|
li +1 |
|
|
|
|
|
|
|
|
|
li |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Xi −1 |
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
Xi + |
|
|
|
|
|
|
Xi +1 |
+ ip |
= 0 . |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EJi +1 |
|
|
|
||||||||||||||||||||||||||||||
|
|
6EJi |
3EJi |
|
|
|
|
3EJi +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Умножая его на произвольное значение 6EJ0 , получим: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
λi Xi −1 + 2(λi |
+ λi +1 )Xi |
+ λi +1Xi +1 + 6EJ0 |
|
ip |
|
= 0 , |
|
(8.23) |
||||||||||||||||||||||||||||||||||||||||
ãäå λi = li J0 – приведенная длина i-го пролета.
Ji
Каноническое уравнение метода сил, записанное в форме (8.23), называется уравнением трех моментов. Оно связывает три последовательных неизвестных опорных момента для двух смежных пролетов с длинами li è li +1 . Смысл i-го уравнения: отсутствие взаимного угла поворота сечений балки на i-ой опоре.
Подчеркнем, что 6EJ0 – произвольная величина. Однако для удобства в качестве J0 принимают момент инерции одного из пролетов балки. Тогда приведенные и реальные длины пролетов имеют одинаковую размерность.
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
43 |

8.7.2 Формула для грузового перемещения. Построим груçî- вую эпюру Mp (рисунок 8.15, ä) и перемножим ее с эпюрой Mi (см. рисунок 8.15, â) по правилу Верещагина:
ip = |
Ωi yCi |
+ |
|
Ωi +1yCi+1 |
, |
|
|
|
|
||||
|
EJi |
|
EJi +1 |
|
||
ãäå Ωi , Ωi +1 – ïëîùадь эпюры Mp |
â i-ì è (i + 1)-м пролетах; yCi – |
|||||
ордината эпюры Mi под центром тяжести Ñi |
эпюры Mp â i-ì |
|||||
пролете; yCi+1 – òî æå, â (i + 1)-м пролете; EJi |
, EJi +1 – жесткости |
|||||
балки в i-ì è (i + 1)-м пролетах. |
|
|
|
|
||
Рассматривая подобные треугольники эпюры Mi , получаем: yCi = ai /li ; yCi+1 = bi +1 /li +1 .
С учетом этого формула для грузового перемещения принимает вид:
ip |
= |
Ωiai |
+ |
Ωi +1bi +1 , |
(8.24) |
|
|
EJili |
|
EJi +1li +1 |
|
ãäå a, b – расстояния от центра тяжести эпюры Mp до левой и правой опор.
8.7.3 Особенности применения уравнений трех моментов. Применение уравнения трех моментов зависит от условий на концах балки.
Шарнирные опоры на концах. В уравнении (8.23) индекс i должен принимать значения 1, 2, ..., (m – 1), ãäå m – номер последнего пролета. При этом количество уравнений достаточно для определения всех неизвестных моментов. В эти уравнения будут входить X0 è Xm – моменты на крайних шарнирных опорах, которые равны нулю (рисунок 8.16, à).
Консоли на концах балки. Удобно отбросить консоли и перенести нагрузку на крайние опоры, заменив ее силами и моментами (рисунок 8.16, á). Затем составить уравнения трех моментов так, как для балки на шарнирных опорах. В отличие от предыдущего случая, моменты X0 è Xm не будут нулевыми. Направлять их следует так же, как и моменты на промежуточных опорах – чтобы были растянуты нижние волокна, а знак определять в соответствии с действием нагрузки на консолях.
Заделки на концах балки. Жесткую заделку необходимо заменить тремя стержнями, скользящую – двумя (рисунок 8.16, â). В результате образуется два дополнительных пролета бесконечно малой длины, позволяющие составить два дополнительных уравнения – 0-е и m-е, как для балки с крайними шарнирными опорами. В эти уравнения будут входить X−1 è Xm +1 – моменты на крайних шарнирных опорах, равные нулю.
44 |
А. В. Яровая Курс лекций по строительной механике. Часть 2 |

Рисунок 8.16
Методика расчета неразрезной балки с помощью уравнений трех моментов имеет несомненное преимущество перед классиче- ским методом сил: чтобы определить коэффициенты канониче- ских уравнений, нет необходимости строить и перемножать единичные эпюры моментов в основной системе.
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
45 |
9 Метод перемещений
9.1Кинематическая неопределимость
9.1.1Идея метода перемещений. В методе сил за неизвестные принимались усилия в лишних связях; для отыскания этих усилий составлялись уравнения совместности деформаций; после
этого устанавливалась картина распределения внутренних сил и моментов, далее определялись перемещения заданных сечений и узлов системы.
Но задача расчета статически неопределимой системы может быть решена и по-другому. В качестве неизвестных можно принять не усилия, а характерные перемещения системы, например, перемещения ее узлов; для их отыскания составить уравнения равновесия; по найденным значениям перемещений установить деформированное состояние конструкции и далее найти внутренние усилия. Такой метод расчета получил название метода перемещений.
9.1.2 Основные неизвестные метода перемещений. В результате различных внешних воздействий сооружение деформируется, его сечения и узлы смещаются. За основные неизвестные метода перемещений примем угловые и линейные перемещения узлов
системы. Будем обозначать их символом Z независимо от типа. Кинематически определимой называется система, у которой
все перемещения узлов определены, либо отсутствуют.
Заметим, что понятия «статическая определимость» и «кинематическая определимость» никак не связаны: статически определимые системы могут быть кинематически неопределимыми и наоборот.
|
Каждый шарнирный узел системы |
|
|
может получать линейное смещение, |
|
|
определяемое на |
плоскости двумя |
|
компонентами – вертикальным и го- |
|
|
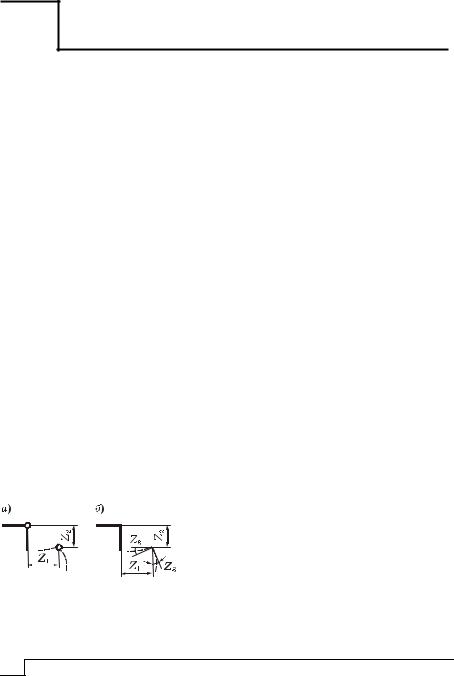
ризонтальным перемещениями Z1 è Z2 |
|
|
(рисунок 9.1, à). |
Каждый жесткий |
|
óçåë, помимо линейного смещения, |
|
Рисунок 9.1 |
может еще и поворачиваться на угол |
|
|
Z3 (рисунок 9.1, á). |
|
В зависимости от расчетной схемы конструкции одно или оба |
||
линейных перемещения могут отсутствовать. |
|
|
46 |
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
|
9.1.3 Степень кинематической неопределимости. Минимальное число тех неизвестных перемещений узлов, знание которых позволяет установить деформированный вид системы (а, следовательно, затем и усилия в ее элементах) называется степенью кинематической неопределимости.
Для плоской стержневой системы степень кинематической неопределимости можно вычислить по формуле:
nê = nó + në , |
(9.1) |
ãäå nó, në – количество независимых угловых и линейных перемещений узлов.
Значение nó равно числу жестких узлов системы.
Величина në зависит от принятых допущений о характере деформирования стержневой конструкции. В общем случае ее можно определить как количество дополнительных стерженьков
(одиночных связей), которые необходимо установить для полной ликвидации линейных смещений узлов.
9.1.4Допущения метода перемещений. Стержневые системы,
êрасчету которых предполагается применять метод перемещений, считаются линейно деформируемыми. Для них сохраняются все гипотезы, принятые ранее.
Для сооружений, в которых перемещения обусловлены преимущественно изгибными деформациями (рам и балок), вводятся дополнительные допущения.
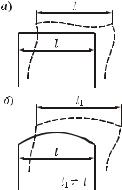
Д о п у щ е н и е 1. При изгибе прямого стержня сближением его концов можно пренебречь, т. е. можно считать, что первона- чальная длина стержня равна длине хорды, стягивающей концы стержня после его искривления (рисунок 9.2, à). Это допущение
вытекает из гипотезы малости деформаций, справедливой для линейно деформируемых систем. Для криволинейных стержней оно не приемлемо (рисунок 9.2, á).
Допущение 2. Продольные деформации стержней за счет растяжения–сжатия малы по сравнению с деформациями изгиба,
поэтому ими можно пренебречь. |
|
Достаточно хорошо это допущение со- |
|
блюдается для рам с вертикальными стой- |
|
ками при небольшом числе этажей. Для |
|
многоэтажных рам, рам с наклонными стой- |
|
ками, арок и ферм продольные деформации |
|
стержней учитывать необходимо. |
Рисунок 9.2 |
|
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
47 |
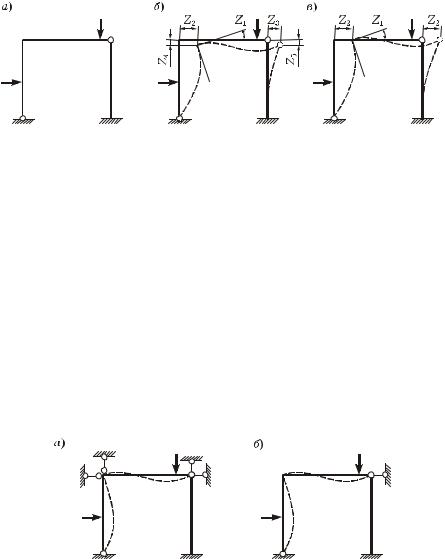
Допустим, требуется найти степень кинематической неопределимости рамы, показанной на рисунке 9.3, à.
Рисунок 9.3
Для установления деформированного вида рамы необходимо знание пяти независимых перемещений узлов (рисунок 9.3, á) – одного углового Z1 (nó = 1) и четырех линейных Z2, ..., Z5 (në = 4). Следовательно, по формуле (9.1)
nê = nó + në = 1 + 4 = 5.
С учетом указанных выше допущений можно считать, что Z3 = Z2, Z4 = 0, Z5 = 0. Тогда nó = 1, në = 1, значит,
nê = 1 + 1 = 2.
Таким образом, количество неизвестных существенно уменьшилось. Для установления деформированного вида рамы достаточно всего двух перемещений – Z1 è Z2 (рисунок 9.3, â).
Рассмотрим, как иначе найти степень кинематической неопределимости. Было указано, что значение nó равно числу жестких узлов системы. Рама содержит один жесткий узел, поэтому nó = 1.
Величину në можно определить как количество дополнительных стерженьков, которые необходимо установить для полной ликвидации линейных смещений узлов. Без использования допущений метода перемещений необходимо узлы закрепить четырьмя стерженьками (рисунок 9.4, à), с учетом допущений – достаточно одного (рисунок 9.4, á).
Рисунок 9.4
Если оба допущения справедливы, то количество независимых линейных перемещений nл можно установить как число степеней
48 |
А. В. Яровая Курс лекций по строительной механике. Часть 2 |

свободы шарнирной схемы Wøàðí, полученной из заданной системы введением полных шарниров во все узлы, включая и опорные; при этом все консоли, если они есть, должны быть отброшены1):
në = Wøàðí . |
(9.2) |
Для определения числа степеней свободы шарнирной схемы удобно использовать формулы (1.4) и (1.5):
Wøàðí = (2Ó −ÑÎ )øàðí ; Wøàðí = (Ø −3Ê)øàðí ,
ãäå Ó – количество шарнирных узлов, непосредственно не связанных с землей; ÑÎ – количество одиночных связей (стержней шарнирной схемы и опорных стержней); Ø – количество шарниров (с учетом кратности), Ê – количество замкнутых контуров.
9.2Основная система метода перемещений
9.2.1Дополнительные связи и цель их введения. При расчете конструкций методом сил отбрасывались лишние связи, и образовывалась статически определимая основная система, в которой возможно построение эпюр от нагрузки и единичных усилий.
В методе перемещений заданная система также преобразуется, но не в статически, а в кинематически определимую. Для этого
вводятся дополнительные связи, устраняющие угловые и линейные перемещения узлов.
Эти связи можно разделить на два вида:
плавающие заделки (защемления), которые накладываются на все жесткие узлы;
одиночные стержни, которые устанавливаются по направлениям возможных линейных смещений узлов.
На рисунке 9.5 показаны варианты изображения одной и той же плавающей заделки на расчетной схеме. Такая заделка не лишает узел линейной подвижности. Она может поступательно пе- 



ремещаться вместе с узлом, но не может поворачиваться до тех пор, пока ей не сообщен принудительный поворот.
Если число дополнительных связей совпадает со степенью кинематической неопределимости сооружения, и все они введены правильно, то все узлы станут неподвижными. В заданной же системе узлы смещаются. Поэтому наложение связей на конст-
1) Консоли всегда статически определимы, поэтому перемещения их концов не входят в число неизвестных метода перемещений.
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
49 |
рукцию необходимо компенсировать дополнительными внешними воздействиями: ее узлам следует придать такие же перемещения, которые имелись изначально. Полученная таким образом система представляет собой основную систему метода перемещений.
Казалось бы, введение дополнительных связей усложняет задачу. Однако это позволяет представить систему как «набор» прямых линейно деформируемых стержней постоянного сечения, которые могут быть по отдельности рассчитаны на любые виды воздействий (силовое, температурное, кинематическое).
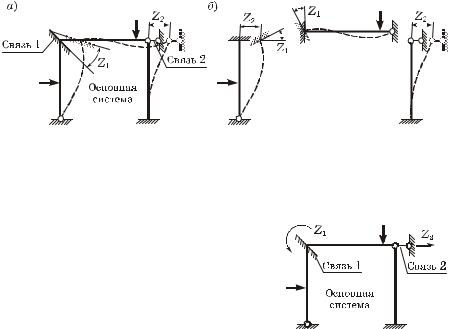
Например, для рамы, показанной на рисунке 9.3, à, основная система получается следующим образом: в жесткий узел вводится плавающая заделка (связь 1), которой придается поворот на угол Z1, а также узлы рамы закрепляются горизонтальным стержнем (связь 2), который принудительно смещается на Z2 (рисунок 9.6, à). Заданная и основная системы эквивалентны: их деформированное состояние, а, следовательно, и внутренние усилия одинаковы.
Теперь каждый элемент рамы можно отделить от остальных и рассчитать отдельно на действующую нагрузку и смещение концов (рисунок 9.6, á).
Рисунок 9.6
Часто деформированное состояние основной системы не показывают, а для перемещений задают лишь направления. Другой способ изображения основной системы для рассмотренной выше рамы показан на рисунке 9.7.
Плавающие заделки накладываются на все жесткие узлы системы, опорные стержни устанавливаются по всем на-
правлениям независимых линейных смещений узлов. Следовательно, основная система метода перемещений
может быть по существу сформирована
единственным образом. Напомним, что в методе сил можно было предложить множество вариантов.
50 |
А. В. Яровая Курс лекций по строительной механике. Часть 2 |
