
mu-soprotivleniye-materialov-z
.pdf
Центральные оси zC, yC надо повернуть против часовой стрелки на угол18,7 , чтобы они стали главными центральными осями u и v.
5. Определим главные центральные моменты инерции сечения
|
|
|
|
|
|
|
J z |
|
J y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1512,01 868,88 |
|
|||
J |
|
|
|
J |
|
|
C |
C |
|
|
(J |
|
|
J |
|
|
|
)2 |
4J 2 |
|
|
|
|
|||||||||||
max |
U |
|
|
|
|
|
|
|
z |
|
y |
|
|
y |
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
C |
|
|
C |
|
|
|
z |
C |
C |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
min |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
(1512,01 868,88)2 4 246,022 |
1190,445 404,833; |
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
J |
max |
J |
u |
1595,33 см4 , |
J |
min |
J |
v |
785,562 см4. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 4 Тема: Изгиб (стр. 237-258)
Для заданных двух схем балок требуется написать выражение для Q и M по участкам в общем виде, построить эпюры Q и M, найти Mmax и подобрать:
а) для схемы «а» деревянную балку круглого поперечного сечения при [ ] 8 МПа ;
б) для схемы «б» – стальную балку двутаврового поперечного сечения при [ ] 160 МПа .
Схема «а» (рис. 4.1)
l1 10a 1,5 м; a1 7a, a2 5a, a3 2a, M 7 кН, P 5 кН ; q 7 кН/м .
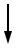 P
P
a1 |
a2 |
l1 =
Рис. 4.1
1. Составляем расчетную схему балки согласно своим исходным дан-
ным (рис. 4.2).
l1 10a 1,5 м, |
a 0,15 м, |
а1 7 0,15 1,05 м, |
а2 5 0,15 0,75 м. |
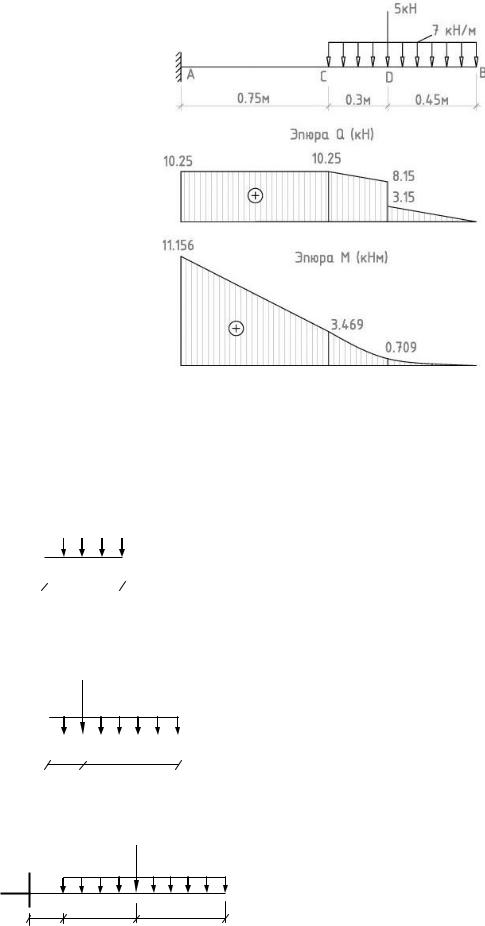
а)
б)
в)
Рис. 4.2
2. Запишем выражение для Q и M по участкам балки.
Участок ВD 0 x 0,45 м
|
|
|
|
|
|
|
|
|
Q 7x; |
|
|||
|
|
|
|
7 кН/м |
|
|
x 0, Q 0; x 0,45 м, Q 3,15 кН |
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
В |
|
|
M 7 |
x2 |
3,5x2 , |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x 0, x 0,45 м , |
М 0,709 кНм |
|||
|
|
|
|
|
|
|
|
|
Участок DC 0 x 0,3 м |
||||
|
|
|
|
5 кН |
|
|
Q 5 7(0,45 x) 8,15 7x |
||||||
|
|
|
|
|
|
x 0, Q 8,15 кН; |
x 0,3 м, Q 10,25 кН . |
||||||
|
|
|
|
|
|
7 кН/м |
|||||||
|
|
|
|
|
|
|
|
В |
M 7 |
(x 0,45)2 |
5x 0,70875 8,15x 3,5x2 , |
||
|
|
|
|
D |
|
|
|
||||||
|
|
|
x |
|
0,45 м |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x 0, M 0,70875 0,709 , |
||
|
|
|
|
x 0,3 м, |
М 0,70875 2,445 0,315 3,46875 3,469 кНм. |
||||||||
Участок СА 0 x 0,75 м
|
|
|
5 |
7 |
|
|
|
|
|
x |
С |
0,3 м |
D |
В |
0,45 |
Q5 7 0,75 10,25 кН
М5(0,3 x) 7 0,75 (0,375 x)
3,469 10,25x,
x 0, M 3,469 кНм.

x 0,75 м, M 11,156 кНм .
3. На основании выполненных расчетов строим эпюры Q и M (рис. 4.2
б, в).
4. Подберем необходимый диаметр круглого поперечного сечения деревянной балки из условия прочности на изгиб (рис. 4.3).
max M z max [ ]; [ ] 8 МПа 0,8кН см2 .
Wz
Сеч. |
y |
8 |
|
|
z Эп. σ
8
d
Рис. 4.3
Из эпюры М значение M z max 11,156 кНм 1115,6 кН см в сечении А
у жесткой заделки. Момент сопротивления Wz для круглого поперечного сечения равен
Wz d 3 . 32
С учетом этого условие прочности на изгиб примет вид
max 32 M z3max [ ].
d
|
|
32 |
M z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
32 1115,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда d |
3 |
|
|
3 |
|
|
3 |
1411,463 24,22 24,5 см. |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
[ ] |
|
3,14 0,8 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
d 24,5 см. |
|
|
|
|
|
|
|
|
||||||
Схема «б» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дано: схема (рис. |
4.4), l2 10a 7 м, |
а2 5а, |
|
а3 2а, |
М 7 кНм, |
||||||||||||||||||||||
q 7 кН м . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
M |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
l2 =10a |
|
a |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
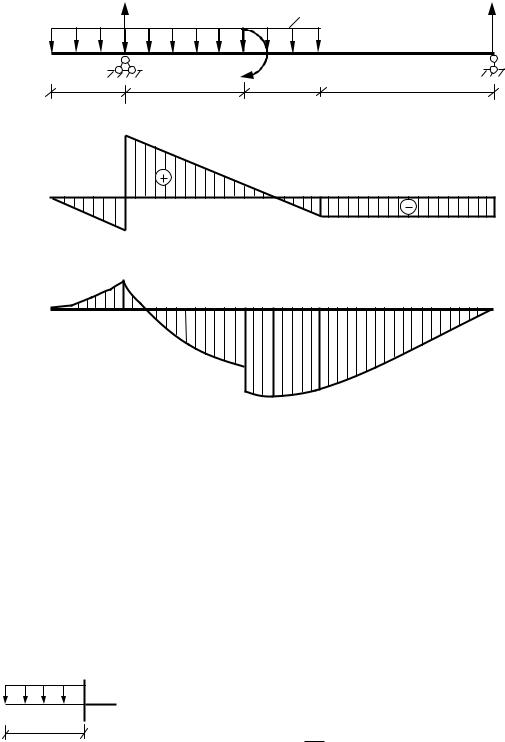
|
|
|
|
|
Рис. 4.4 |
|
|
||
|
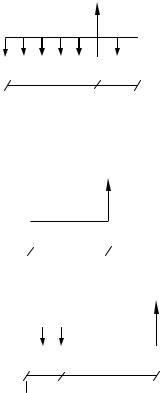
1. Составим расчетную схему балки согласно своим исходным данным |
||||||||
(рис. 4.5, а). |
|
|
|
|
|
|
|
||
|
l2 10a 7 м, а 0,7 м, |
|
|
|
|
|
|||
|
а1 7 0,7 4,9 м, |
а2 |
5 0,7 3,5 м, а3 |
2 0,7 1,4 м. |
|||||
|
|
RA= 28,155 |
|
|
|
|
|
|
RB= 6,145 кН |
|
|
|
|
|
7 кНм |
7 кН/м |
|
|
|
|
а) |
|
|
|
|
|
|
|
B |
|
C |
А |
|
|
D |
|
Е |
|
|
|
|
|
|
|
|
||||
|
|
1,4 м |
2,1 м |
1,4 м |
|
3,5 м |
|||
|
|
18,355 |
|
|
|
|
|
|
|
|
|
|
|
|
Эп. Q (кН) |
|
|||
|
б) |
|
|
|
|
|
|
|
|
|
|
9,8 |
|
|
|
6,145 |
|
6,145 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6,86 |
|
|
Эп. М |
|
|
||
|
в) |
|
|
|
|
|
|
|
0 |
|
|
|
16,25 |
|
|
|
|
||
|
|
|
|
23,25 |
21,508 |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
24,20 |
|
|
|
|
|
|
|
|
|
Рис. 4.5 |
|
|
||
|
2. Определим величину опорных реакций |
|
|||||||
|
|
M A 0 |
7 4,9 1,05 7 7RB 0 |
RB 6,145 кН. |
|||||
|
|
M B 0 |
7 7 4,9 5,95 7RA 0 |
RA 28,155 кН . |
|||||
|
Проверка. y 28,155 |
6,145 7 4,9 34,3 34,3 0. |
|||||||
|
3. Запишем выражения для Q и M по участкам балки. |
||||||||
|
|
|
Участок СА |
0 x 1,4 м |
|
||||
|
7 кН/м |
|
|
|
Q 7x ; |
|
|
|
|
|
|
|
|
|
x 0, |
Q 0; |
x 1,4 м, Q 9,8 кН. |
||
С |
x |
|
|
|
M 7 x |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3,5x2 |
, |
|||
|
|
|
|
|
|
2 |
|
|
|
x 0, M 0; x 1,4 м, M 6,86 кНм.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок AD |
0 x 2,1м |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q 7(1,4 x) 28,155 18,355 7x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0, |
Q 18,355 кН; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
28,55 кН |
x 2,1м, |
Q 3,655 кН. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(1,4 x)2 |
|
|
|||||||
|
|
|
7 кН/м |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 7 |
|
|
6,86 18,355x 3,5x2 |
; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
С |
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1,4 |
|
|
|
|
|
|
|
|
x 0, |
M 6,86 кНм; |
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2,1м, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 6,86 38,546 15,4365 16,251кНм. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок ВЕ |
0 x 3,5 м |
|
|
||||
|
|
|
|
|
|
|
|
|
|
6,145кН |
Q 6,145 кН, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
В |
M 6,145x. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
|
|
x 0, |
M 0, x 3,5 м, |
M 21,508 кНм. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок ED |
0 x 1,4 м |
|
|
||||
|
|
7 кН/м |
|
|
|
|
|
|
|
6,145кН |
Q 6,145 7x ; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
x 0, |
Q -6,145кН; |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
Е |
3,5м |
|
x 1,4 м, |
Q 3,655 кН. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поперечная сила на этом участке меняет знак, значит, существует экстремум для изгибающего момента.
6,145 7x 0, |
x 0,878 м . |
M 6,145(3,5 x) 7 |
x2 |
21,5075 6,145x 3,5x2 ; |
|||||||||||||||
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x 0, M 21,508 кНм; |
|||||||||||||||||
x 1,4 м, |
M 21,5075 8,603 6,86 23,251кНм; |
||||||||||||||||
x 0,878 м, |
M max 24,205 кНм. |
||||||||||||||||
4. На основании выполненных расчетов строим эпюры Q и М (рис. 4.5, |
|||||||||||||||||
б, в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Определим требуемый момент сопротивления поперечного сечения |
|||||||||||||||||
из условия прочности на изгиб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
max |
[ ], |
||||||||
|
|
M z |
|
||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Wz |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M z |
|
max . |
||||||||||
|
W |
z |
|
|
|
|
|
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
[ ] |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||

Из эпюры M значение M z max 24,205 кНм 2420,5 кН см. [ ] 160 МПа 16кН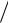 см2 .
см2 .
Wz 2420,5 151,3 см3. 16
6. Обращаемся к сортаменту прокатной стали и выбираем необходимый номер двутавровой балки с моментом сопротивления, близким к требуемому.
Наиболее близко подходят двутавры №18 с Wz 143 см3 и № 18а с Wz 159 см3.
При установке двутавра №18 будет некоторое перенапряжение. Оценим его величину.
|
|
|
|
M z |
max |
|
2420,5 |
|
16,93 кН см2 =169,3 МПа. |
||
max |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
Wz |
143 |
|
|
|||||
|
|
|
|
|
|
||||||
%перенапряжения |
169,3 160 |
100 5,8% 3%, что недопустимо. |
|||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
160 |
|
|
|
Окончательно выбираем двутавр №18а с Wz 159 см3. В этом случае максимальное напряжение будет равно
|
|
|
|
M z |
max |
|
2420,5 |
15,22 кН см2 =152,2 МПа<[σ]=160 МПа. |
max |
|
|
|
|||||
|
|
|
|
|||||
|
|
|
Wz |
159 |
|
|||
|
|
|
|
|
||||
Задача 5 Тема: Косой изгиб (стр.258-262)
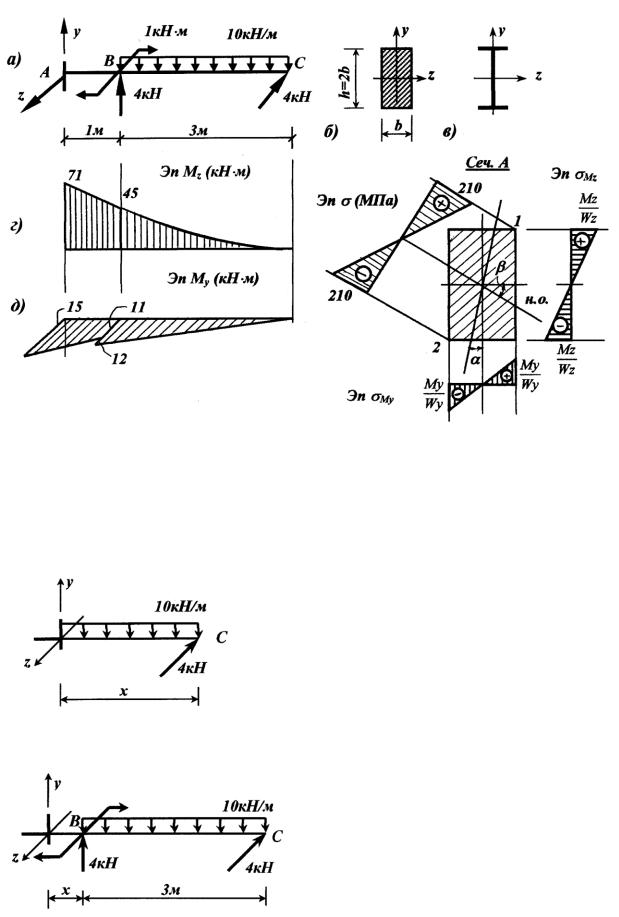
Определить размеры поперечных сечений стальной балки, найти положение нейтральной оси и построить эпюру нормальных напряжений в опасном прямоугольном сечении для балки, изображенной на рис. 5.1. Принять R 210 МПа , а нагрузки – расчетными.
е)
Рис. 5.1
Запишем выражения для Mz и My по участкам балки и вычислим их значения для характерных сечений
Участок СВ |
0 х 3 м |
|
|||||
|
М |
|
10 |
x2 |
5x2 . |
||
|
z |
|
|||||
|
|
|
2 |
|
|
||
|
|
|
|
|
|
||
|
x 0, M z |
|
0; |
x 3 м, М z 45 кНм . |
|||
|
М у 4х. |
|
|||||
|
х 0, М у 0; |
х 3 м, М у 12 кНм . |
|||||
Участок ВА |
0 х 1м |
|
|||||
|
|
М z 10 3(1,5 х) 4х 45 26 х. |
|||||
|
|
x 0, |
M z 45 кНм; |
||||
|
|
х 1 м, |
|
M z |
71кНм. |
||
Му 4(3 х) 1 11 4х;

х 0, М у 11кНм; х 1м, М у 15 кНм.
1.На основании выполненных расчетов строим эпюры Мz и Mу
(рис. 5.1, г, д).
2.Анализируем эпюры Мz и Mу и устанавливаем, что наиболее опасным сечением является сечение А у жесткой заделки, где Мz и Mу имеют максимальные по абсолютной величине значения, а опасными точками (см. рис. 5.1, е) являются точки 1 и 2. В точке 1 будут наибольшие растягивающие, а в точке 2 – наибольшие сжимающие напряжения. На сечение смотрим по направлению оси х.
3.Определим положение нейтральной оси. След плоскости действия
результирующего изгибающего момента определяется углом и проходит через 1-й и 3-й квадранты.
|
tg |
|
|
M y |
|
|
15 |
|
0,2113; |
|
arctg0,2113 12 . |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
M z |
|
71 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Положение нейтральной оси определяется |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
tg |
|
J z |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
bh3 |
|
b(2b)3 |
|
|
2 |
|
|
|
|
|
|
|
|
J y |
hb3 |
|
2b b3 |
1 |
|
|||||||||
|
|
|
|
|
|
b4 ; J |
|
|
|
b4 ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
J |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||||
12 |
|
12 |
|
3 |
12 |
12 |
6 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
tg 0,2113 |
2b4 6 |
0,2113 4 0,8452; |
|
|
|||||||||||||||||||||||
|
|
|
|
3 b4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
arctg0,8452 39 .
5.Определим из условия прочности по предельным состояниям величину размеров прямоугольного поперечного сечения.
Наиболее опасные точки 1 и 2, но для материалов, одинаково сопротивляющихся растяжению и сжатию, они равноопасны. Остановимся на точке 1.
max 1 M z M y R.
Wz Wy
Для прямоугольного поперечного сечения моменты сопротивления будут равны:
|
|
|
bh |
2 |
|
b(2b)2 |
|
2 |
b3; W |
|
|
hb2 |
2b b2 |
1 |
b3. |
||
W |
z |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
6 |
|
6 |
3 |
6 |
6 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||

3M |
z |
|
3M y |
R; |
1,5M |
z |
|
3M y |
R. |
2b3 |
b3 |
|
b3 |
|
|
b3 |
|
||
b 3 1,5M z 3M y ;
R
М z 71 кНм 7100 кН см.
M y 15 кН м 1500 кН см.
R 210 МПа 21кН см2 .
b 3 1,5 7100 3 1500 8,98 см 9 см.
21
h 2b 18 см .
Определим требуемый номер двутавровой балки.
Предварительно необходимо задаться соотношением
Для средних номеров двутавра Wy 10.
Wz
M |
z |
|
M y |
R; |
M |
z |
|
M y |
R; |
|
|
|
|
|
|
||||
Wz |
Wy |
|
Wz |
0,1Wz |
|
||||
Wy . Wz
W |
M z 10M y |
|
7100 10 1500 |
1052,4 см3. |
|
|
|
|
|||
z |
R |
|
21 |
|
|
|
|
|
|
||
Обращаемся к сортаменту прокатной стали и выбираем номер двутавра с близким к требуемому моментом сопротивления. Наиболее близко подхо-
дит двутавр № 45 с W 1231см3 и |
W |
y |
101cм3. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверим подобранный двутавр: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
M |
z |
|
M y |
|
|
7100 |
|
1500 |
5,768 14,851 |
20,619 |
кН |
|
|
|
||||||
max |
|
|
|
|
|
|
|
|
|
|
см |
2 |
|||||||||||
|
|
Wz |
Wy |
|
|
1231 |
|
|
101 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
206,19 МПа R 210 МПа.
Прочность обеспечена. Окончательно выбираем к установке двутавр № 45.

Задача 6 Тема: Внецентренное сжатие (стр. 262-266)
Чугунный короткий стержень, поперечное сечение которого изображено на рисунке (рис. 6.1), сжимается продольной силой P, приложенной в точке А. Требуется:
1)вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через P, и размеры сечения;
2)найти допускаемую нагрузку Р при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие [σc] и на растяжение [σр].
Дано: схема (рис. 6.1), a 3 см, b 6 см, [ c ] 88 МПа; [ р ] 21 МПа.
b |
A |
2b |
b |
a a
Рис. 6.1
1.Изобразим расчетную схему поперечного сечения согласно своим исходным данным (рис. 6.2).
2.Определим значения главных центральных моментов инерции.
Одна из главных центральных осей – это ось z, совпадающая с осью симметрии.
Для определения второй необходимо найти положение центра тяжести относительно оси y1.
а) разбиваем сечение на простейшие фигуры.
A 3 24 72 см2 , |
A 3 12 36 см2 , |
A A A 108 см2. |
||||||||||||||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
б) координаты центров тяжести составляющих частей относительно |
||||||||||||||||
оси y1 равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
3 |
1,5 см; |
z |
|
3 |
3 |
|
4,5 см, |
|
|||||
|
|
|
2 |
|
|
|||||||||||
|
|
1 |
2 |
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
c |
|
A1z1 A2 z2 |
|
72 1,5 36 4,5 |
2,5 см. |
||||||||||
|
|
|||||||||||||||
|
|
|
A1 A2 |
|
|
108 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
в) проводим через найденное положение центра тяжести вторую главную центральную ось y, перпендикулярную оси z.
