
mu-soprotivleniye-materialov-z
.pdf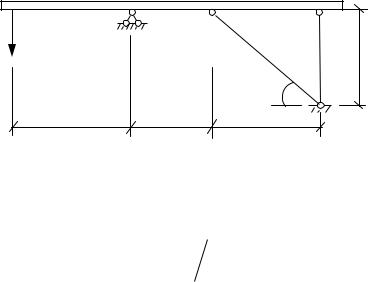
Методические рекомендации к практической подготовке по дисциплине "Сопротивление материалов"
для студентов-заочников специальности 1-70 04 03 "Водоснабжение, водоотведение и охрана водных ресурсов"
Отмена контрольных работ не отменяет умение производить расчеты на прочность, жесткость и устойчивость элементов строительных конструкций.
Для успешной сдачи экзамена по сопротивлению материалов студенты специальности 1-70 04 03 должны уметь решать задачи, примеры решения которых приведены ниже. В скобках указаны теоретические материалы по данной теме из: Сопротивление материалов: Учеб.-метод. комплекс для студ. спец. 1-70 04 -2 "Теплогазоснабжение, вентиляция и охрана воздушного бассейна", 1-70 04 03 "Водоснабжение, водоотведение и охрана водных ресурсов"/ Сост. В.К. Родионов; Под общ. Ред. Л.С. Турищева. – Новополоцк:
ПГУ, 2005. -364 с.
Вопросы для самоконтроля и рекомендованные для самостоятельного решения задачи также находятся в указанном УМК.
Задача 1 Тема: статически неопределимые задачи на растяжение (стр. 212-
236)
Абсолютно жесткий брус опирается на шарнирно-неподвижную опору
иприкреплен к двум стержням при помощи шарниров. Требуется:
1)найти усилия и напряжения в двух стержнях, выразив их через силу
Q;
2)найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [ ] 160 МПа;
3)найти предельную грузоподъемность Qтк и допускаемую нагрузку Qдоп, если предел текучести т 240 МПа и запас прочности k 1,5;
4)сравнить величины Qдоп, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам.
Дано: A 15 см2, а 2,7 м; b 2,5 м; с 1,7 м.
A |
B |
|
C |
Q |
|
A |
|
|
|
1 |
2 |
|
|
α |
|
a = 2,7 м |
c = 1,7 м |
b = 2,5 м |
|
2A
b
D
Рис. 1.1
1. Определим недостающие геометрические параметры, необходимые для дальнейшего расчета.
45 ; sin 45 cos45 0,707; |
l |
b |
sin 45 |
2,5 |
м. l |
|
b 2,5м . |
|
2 |
||||||
|
|||||||
|
1 |
|
|
sin 45 |
|
|
|
|
|
|
|
|
|
|
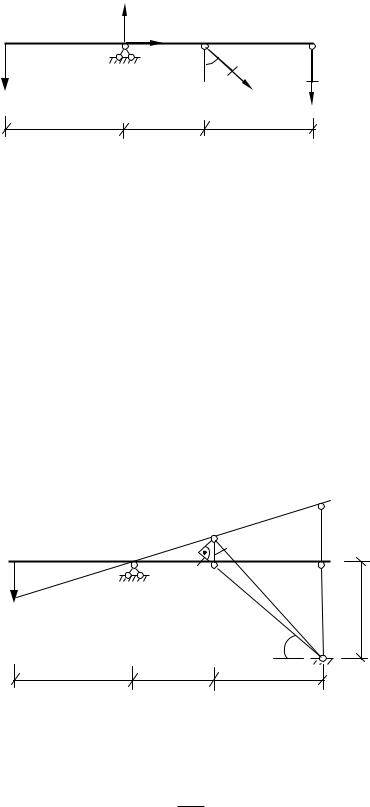
2. Изобразим план и определим степень статической неопределимости. План сил согласовываем с характером деформации системы.
RAy
RAx
A |
B |
|
C |
Q |
|
45º N1 |
N2 |
|
|
|
|
2,7 м |
1,7 м |
2,5 м |
|
Рис. 1.2
Всего неизвестных 4 (RAX, RAY, N1, N2), а уравнений статики для данной произвольной плоской системы сил можно составить только 3. Следовательно, данная система 4 3 1 раз статически неопределима.
3. Составим необходимое уравнение равновесия (статики). Для дальнейшего расчета нам необходимо определить значения усилий в стержнях N1 и N2, поэтому составим такое уравнение статики, в которое войдут только эти неизвестные.
M A 0. 2,7Q 1,7N1 cos 45 4,2N2 0
|
1,2019 N1 4,2N2 |
2,7Q . |
|
(1) |
|
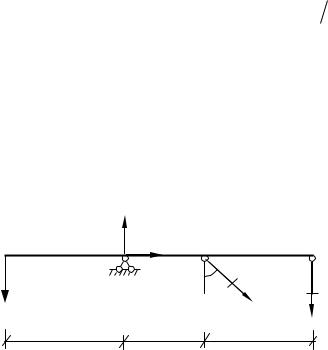
4. Изобразим диаграмму перемещений (рис. 1.3) и составим дополни- |
|||||
тельное уравнение совместности деформаций. |
|
|
|||
|
|
|
|
δС =Δl2 |
|
|
|
|
δB |
|
|
|
A |
l1 B |
|
C |
|
Q |
|
|
2A м |
||
|
|
A 1 |
|
||
|
|
|
2 |
2,5 |
|
|
|
|
|
45º |
D |
|
2,7 м |
1,7 м |
2,5 м |
|
|
Рис. 1.3
Из подобия треугольников
C 4,2 .
B 1,7
Заменим перемещения узлов абсолютными деформациями стержней
|
|
|
|
|
C l2 , B |
l1 |
, |
|
|
|
|
|
sin 45 |
||
|
|
|
|
|
|
|
|
l |
2 |
sin 45 |
4,2 |
|
|
|
|
|
|
|
|
(уравнение совместности деформаций). |
|||
|
|
l |
1,7 |
||||
|
|
1 |
|
|
|
|
|
Выразим абсолютные деформации стержней по закону Гука.
l |
2 |
|
N2l2 |
|
N2 |
2,5 |
; |
l |
|
|
N1l1 |
|
|
N1 2,5 |
; |
||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
EA2 |
|
2EA |
1 |
|
|
|
EA1 |
|
EAsin 45 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2,5N |
2 |
sin 2 45 EA |
|
4,2 |
|
|
|
|
|
|
|
4,2 4N |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
; N |
2 |
|
|
|
|
|
1 |
9,8824N . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2EA 2,5N1 |
|
1,7 |
|
|
|
|
1,7 |
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
N2 9,9924 N1 . |
|
|
(2) |
|||||||||||
5. Решаем совместно уравнения (1) и (2).
1,2019 N1 4,2 9,8824 N1 2,7Q ,
N1 0,0632 Q ,
N2 0,6248 Q .
6. Определим напряжения в стержнях (1) и (2).
N1 |
0,0632Q |
; |
|
N2 |
0,6248Q |
0,3124Q ; |
||||||||
1 |
A1 |
|
A |
|
2 |
|
A2 |
|
2A |
|
A |
|
||
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
max |
0,3124Q |
. |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
||
7. Определим величину допускаемой нагрузки из условия прочности по допускаемым напряжениям.
|
|
|
0,3124Q |
[]; |
|
[ ] 160 МПа 16 кН см2 . |
||||
max |
|
|
||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
А[ ] |
|
|
15 16 |
768,24 кН. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
доп |
0,3124 |
|
|
0,3124 |
|
||
|
|
|
|
|
|
|
||||
Qдоп 768б24 кН .
8. Изобразим схему в предельном состоянии, соответствующем исчерпанию несущей способности, когда напряжения в двух стержнях достигнут предела текучести (рис. 1.4).
RAy
RAx
A |
B |
|
C |
Qтк |
|
45º |
|
|
N1пр=σт·2 |
N2 = 2σт·2 |
|
|
|
||
2,7 м |
1,7 м |
2,5 м |
|
Рис. 1.4
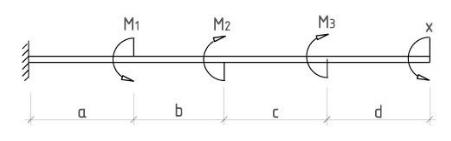
9. Составим уравнения равновесия в предельном состоянии и определим предельную грузоподъемность системы и значение допускаемой нагруз-
ки Qдоп.
2,7Qк |
1,7 |
т |
Аcos45 4,2 2 |
т |
A 0, |
|||||||||
т |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2,7Qк 9,6019 |
т |
А 0, |
|
|
|||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
||
Qк 3,5563 |
т |
А 3,5563 24 15 1280,27кН . |
||||||||||||
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
Qк |
|
1280, 27 |
|
|
|
|
|
|||
|
|
т |
|
|
|
|
853,5 кН . |
|||||||
|
|
|
|
|||||||||||
доп |
|
|
К |
|
1,5 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
10. Сравним величины Qдоп, полученные при расчете по допускаемым нагрузкам и допускаемым напряжениям.
Величина допускаемой нагрузки, полученная при расчете на прочность по допускаемым нагрузкам, больше величины допускаемой нагрузки из расчета на прочность по допускаемым напряжениям в
Q |
|
853,5 |
|
|
|
доп |
|
|
1,11 |
раз. |
|
Qдоп |
768,24 |
||||
|
|
|
Задача 2 Тема: Кручение (стр. 229-236)
К стальному валу приложены три известных момента: M1, M2, M3 (рис. 2.1). Требуется:
1)установить, при каком значении момента X угол поворота правого концевого сечения вала равен нулю;
2)для найденного значения Х построить эпюру крутящих моментов;
3)при заданном значении [τ] определить диаметр из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;
4)построить эпюру углов закручивания;
5)найти наибольший относительный угол закручивания (на 1 м длины). Дано: a 1,7 м, b 1,5 м, с 1,7 м ,
M1 1,7 кНм, M 2 1,5 кНм, М 3 1,7 кНм , [ ] 55 МПа.
Рис. 2.1

1. Установить, при каком значении момента X угол правого концевого сечения B равен нулю.
|
B |
|
M1a |
|
M 2 (a b) |
|
M3 (a b c) |
|
X (2a b c) |
0, |
|
|
|
|
|||||||
|
|
GJ |
|
GJ |
|
GJ |
|
GJ |
||
|
|
|
|
|
|
|||||
X M1a M 2 (a b) M 3 (a b c) 2a b c
2,89 4,8 6,6
1,7 1,7 1,5(1,7 1,5) 1,7(1,7 1,5 1,7) 2 1,7 1,5 1,7
8,33 1,552кНм.
а)
б)
в)
Рис. 2.2
2. Определить значения крутящих моментов по участкам, используя метод сечений, и построить эпюру крутящих моментов (рис. 2.2, б).
Т1к 1,552 1,7 1,5 1,7 0,052 кНм, Т 2к 1,552 1,7 1,5 1,648 кНм,

Т3к 1,552 1,7 0,148 кНм,
Т4к 1,552 кНм.
3.Определим требуемый диаметр стального вала круглого поперечного сечения из условия прочности при кручении.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
Tк |
|
|
max |
|
[ ]. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ ] 55 МПа 5,5кН см2 . |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Из эпюры Т |
|
Тк |
|
|
max 1,648кНм 164,8 кН см. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Полярный |
|
|
|
|
момент |
сопротивления |
|
круглого поперечного сечения |
|||||||||||||||||||||||||||||||||||||||||||||||||||
W |
d 3 |
. С учетом этого условие прочности примет вид |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
16 |
|
Tк |
|
max |
|
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
Tк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
16 164,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Отсюда |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
152,681 5,35см. |
Принимаем |
||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3,14 5,5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d 60 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
4. Построим эпюру углов закручивания. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
а) определим жесткость вала при кручении |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
GJ G |
d |
4 |
|
|
G 8 104 МПа 8 103 кН см2 ; |
d 6 см. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3,14 64 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
GJ 8 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101,7356 10 |
|
кН см |
|
. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
б) определим угол закручивания правого крайнего сечения первого уча- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
стка относительно левой жесткой заделки, где A 0. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
T1кl1 |
|
|
0 |
0,052 100 170 |
0,00087 рад. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
GJ |
|
|
|
|
|
|
|
|
101,736 104 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
в) угол закручивания крайнего правого сечения на втором участке |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
T2кl2 |
0,00087 |
1,648 100 150 |
0,00087 0,023430 0,02343рад. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
GJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101,736 104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
г) угол закручивания на конусе третьего участка |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
T3кl3 |
0,02343 |
0,148 170 100 |
0,02343 0,00247 0,02590 рад. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
GJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101,736 104 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
д) угол закручивания на конце четвертого участка |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
T4кl4 |
|
|
|
0,02590 |
1,552 100 170 |
0,02590 0,0259 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
GJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101,736 104 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
На основании выполненных расчетов строим эпюру υ (рис. 2.2, в). 5. Определим наибольший относительный угол закручивания.
Для вала постоянного поперечного сечения он будет на участке с максимальным по модулю крутящим моментом (т.е. на втором участке).
Его можно определить:
1) по эпюре углов закручивания
max |
|
0,02343 0,00087 |
0,0162 |
рад |
0,0162 |
180 |
0,93 |
|
град |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1,5 |
|
|
|
|
м |
|
|
|
3,14 |
|
|
|
м |
|
|
2) по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
max |
|
Tк |
|
max |
100 |
|
1,648 100 100 |
0,0162 |
рад |
0,93 |
град |
|
. |
|
|||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
GJ |
101,736 104 |
м |
м |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Задача 3 Тема: Геометрические характеристики плоских сечений (стр. 102-
112)
Для заданного поперечного сечения, состоящего из прокатных профилей, требуется определить положение главных центральных осей и вычислить главные центральные моменты инерции.
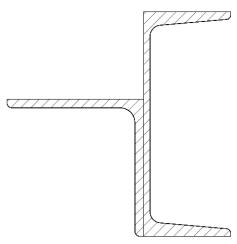
Схема (рис. 3.1), швеллер № 18, уголок 125×125×12
Рис. 3.1
1. Вычерчиваем прокатные профили и выписываем из сортамента все необходимые для расчета геометрические характеристики.
Швеллер № 18 (рис. 3.2, а)
h1 = 180 мм, b1 = 70 мм
d = 5,1 мм, t1 = 8,7 мм, А1 = 20,7 см2,
J |
z |
01 |
1090см4 |
, J |
y |
01 |
86см4 |
, z |
0 |
1,94 см. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
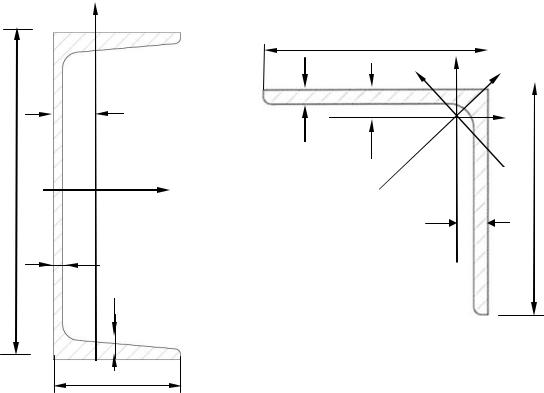
Центральный момент инерции сечения относительно центральных осей z01y01, которые являются главными центральными, J z01 y01 0.
Уголок равнобокий 125×125×12 (рис. 3.2, б)
b 125 мм, d 12 мм, |
А 28,9 см2. |
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
J |
z |
02 |
J |
y |
02 |
422 см4 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J |
max |
670 см4 , |
J |
min |
174 см4 . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z0 y0 3,53 см. |
|
|
|
|
|
|
|
|
||||||||||
Центробежный момент инерции |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
J |
z |
|
y |
|
|
|
J max J min |
|
670 174 |
248 см4 . |
|
|
|
|
|
|
|
|
02 |
02 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y01 |
|
|
|
|
|
|
|
|
|
||
h1
|
|
|
b2 |
y02 |
|
max |
|||
|
|
|
|||||||
|
|
|
|
min |
|
||||
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z02 |
|||
|
|
|
|
|
|
|
|
||
|
|
d |
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
C1 |
Z01 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
b |
||
|
|
|
|
|
|
|
2 |
||
|
|
|
|
|
z0 |
|
|
|
|
d
t
a) |
b1 |
б) |
|
Рис. 3.2
2. Определим положение центра тяжести сечения (рис. 3.3). а) выбираем вспомогательные оси z и y;
б) вычисляем площадь всего сечения
A 20,7 см2 |
; |
A 28,9 см2 |
; |
A 20,7 28,9 49,6 см2. |
1 |
|
2 |
|
|
в) вычислим координаты центров тяжести каждого профиля относительно вспомогательных осей zy.
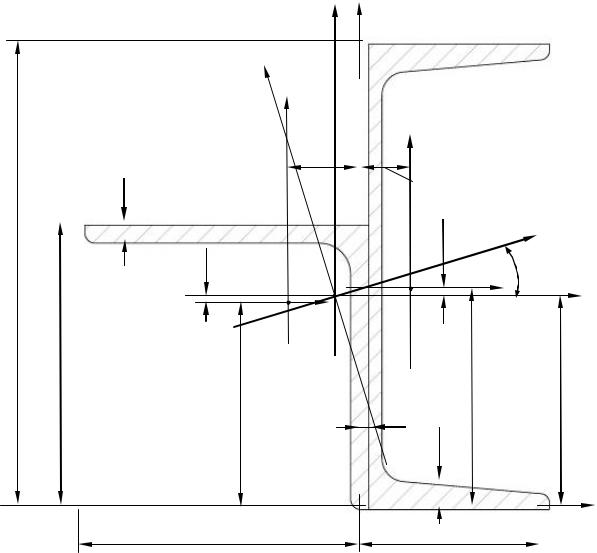
z z |
0 |
1,94 см ; |
у |
h1 |
|
18 |
9 см ; |
||
|
|
||||||||
1 |
|
|
1 |
2 |
2 |
|
|||
|
|
|
|
|
|
||||
z2 z0 353 см ; |
y2 b y0 12,5 3,53 8,97 см. |
||||||||
|
|
|
|
|
yC |
|
y |
||
|
|
|
|
|
V(min) |
|
|
|
|
|
|
|
y02 |
|
|
|
|
|
|
z2 =35,3 |
|
|
12 |
|
|
|
|
180 |
|
|
|
=0,12 |
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
2C |
|
C |
|
|
|
|
y |
|
|
|
|
|
|
|
C2 |
z02 |
125 |
|
|
|
89,7 |
||
|
|
|
|
|||
|
|
|
|
|
= |
|
|
|
|
|
|
z |
|
|
|
|
|
|
y |
|
125
Рис. 3.3
y01 |
|
||
z1 =19,4 |
|
||
= 0,18 |
|
|
U(max) |
1C |
|
||
y |
|
||
|
|
|
18,7º |
C1 |
|
|
z01 |
|
|||
|
|
|
zC |
|
= 90 |
89,82 |
|
5,1 |
1 |
= |
|
|
y |
2 |
|
|
|
|
y |
|
8,7 |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
70 |
||
|
|
||
|
|
|
|
г) вычисляем статические моменты каждого профиля и всего сечения относительно осей z и y.
S |
(1) |
A y |
20,7 9 |
186,3 см3; |
S (2) |
A |
y |
2 |
28,9 8,97 259,23 см3 |
; |
|
|||||
|
z |
1 |
1 |
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
S |
z |
S |
(1) |
S (2) |
186,3 259,23 445,53 см3 ; |
|
|
|||||
|
|
|
|
|
z |
z |
|
|
|
|
|
|
|
|
||
S (1) |
A z |
20,7 |
1,94 40,16 см3; |
S (2) |
A |
z |
2 |
28,9 353 102,02 см3 |
; |
|||||||
y |
|
1 1 |
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
S |
y |
S |
(1) |
S (2) |
40,16 102,02 |
61,86 см3. |
|
|
||||
|
|
|
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
д) вычислим координаты центра тяжести сечения
z |
|
|
S y |
|
61,86 |
1,247 см; y |
|
|
S |
z |
|
445,53 |
8,928 см. |
|
C |
A |
49,6 |
C |
A |
49,6 |
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
3. Определяем моменты инерции сечения относительно центральных |
||||||||||||||
осей zCyC, параллельных осям z и y.
a) через центр тяжести сечения проводим оси zC и yC параллельно соответствующим исходным осям z и y.
б) вычислим координаты центров тяжести ziC, yiC каждого профиля относительно центральных осей zC и yC.
z1C z1 zC 1,94 1,247 3,187 см ,
z2C z2 |
ZC 3,53 1,247 2,283 см , |
y1C y1 |
yC 9 8,982 0,018 см , |
y2C y2 |
yC 8,97 8,982 0,012 см. |
в) вычислим осевые и центробежные моменты инерции каждого профиля относительно центральных осей:
J (1) |
J |
z01 |
y 2 |
A 1090 0,0182 |
20,7 1090,007 см4 , |
|
|
zC |
|
1C |
1 |
|
|
|
|
J (2) J |
z02 |
y 2 |
A 422 ( 0,012)2 |
28,9 422,004 см4 |
, |
||
zC |
|
2C 2 |
|
|
|
||
|
J |
(1) |
J |
y 01 |
z2 |
|
A 86 3,1872 20,7 296,25 см4 , |
|
|||||||||||||||
|
|
y C |
|
|
|
|
1C |
1 |
|
|
|
|
|
|
|
|
|||||||
|
J |
(2) |
J |
y 02 |
z2 |
|
A |
422 ( 2,283)2 28,9 572,63 см4 , |
|
||||||||||||||
|
|
y |
C |
|
|
|
|
2C |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J (1) |
J |
z 01 y 01 |
z |
|
|
|
y |
|
|
A 0 3,187 0,018 20,7 1,19 см4 |
, |
||||||||||||
z C y C |
|
|
|
|
|
|
1C |
|
|
1C |
|
1 |
|
|
|
|
|||||||
J (2) |
J |
|
02 y02 |
z |
|
|
y |
A |
248 ( 2,283) ( 0,012) 28,9 |
||||||||||||||
zC yC |
|
|
|
z |
|
|
|
2C |
|
|
|
2C |
|
|
2 |
|
|
|
|
|
|||
248 0,792 247,21 см4 , |
|
|
|
|
|
||||||||||||||||||
|
J |
zC |
|
J (1) |
J |
(2) 1090,007 422,004 1512,01см4 , |
|
||||||||||||||||
|
|
|
zC |
|
|
|
zC |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
J |
yC |
J |
(1) |
|
J (2) |
296,25 572,63 868,88 см4 , |
|
|||||||||||||||
|
|
|
y |
C |
|
|
|
|
y |
C |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
J |
|
|
|
J (1) |
|
|
|
J |
(2) |
|
1,19 247,21 246,02 см4 . |
|
||||||||||
|
|
z C y C |
|
|
z C y C |
|
|
|
z C y C |
|
|
|
|||||||||||
4. Определим положение главных центральных осей инерции попереч- |
|||||||||||||||||||||||
ного сечения uv. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2Jz y |
|
|
|
|
|
2 ( 246,02) |
|
|||||||
|
|
tg 2 |
|
|
|
|
C C |
|
|
|
|
|
0,7651; |
|
|||||||||
|
|
Jz |
|
J y |
|
|
1512,01 868,88 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 37,4 ; |
18,7 . |
|
|||||||||
