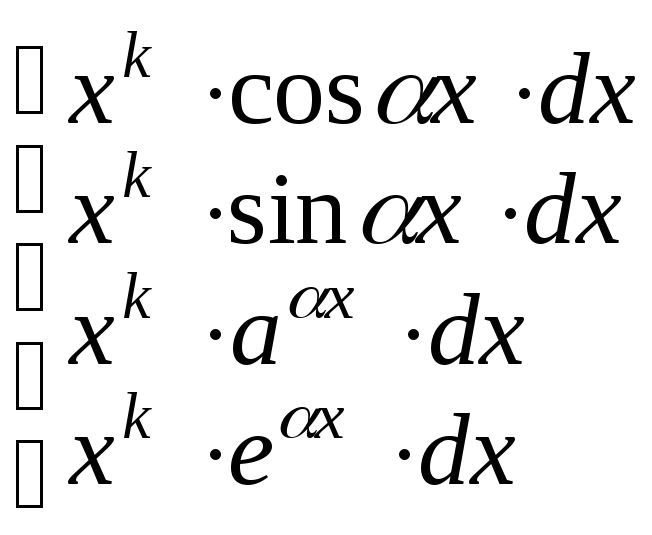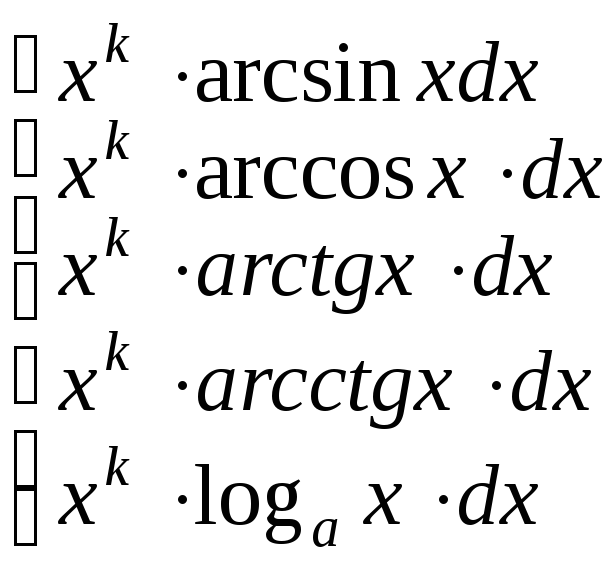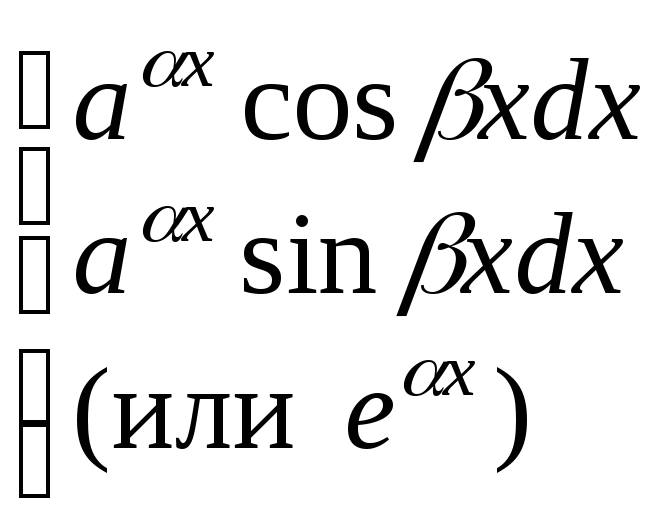- •Министерство образования и науки Украины
- •С о д е р ж а н и е
- •В в е д е н и е
- •I. П о н я т и е и н т е г р а л а
- •1.1. Неопределенный интеграл.
- •Основные свойства неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •Определенный интеграл. Формула Ньюбона-Лейбница. Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •II. М е т о д ы и н т е г р и р о в а н и я
- •2.1. Метод непосредственного интегрирования
- •2.2. Метод замены переменной
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных дробей
- •2.5. Интегрирование некоторых иррациональных функций
- •2.6. Интегрирование тригонометрических функций
- •Примеры.
- •6) Случай универсальной подстановки .
- •2.7. Несобственные интегралы
- •Ііі. Задания для индивидуального решения
- •3.1. Метод непосредственного интегрирования
- •3.2. Метод замены переменной
- •3.3. Метод интегрирования по частям
- •3.4. Интегрирование рациональных дробей
- •3.5. Интегрирование иррациональных функций
- •3.6. Интегрирование тригонометрических функций
- •Несобственные интегралы
2.3. Интегрирование по частям
|
Теорема 4. |
Если
функции
|
Смысл
этой формулы состоит в том, что в ней
интеграл от произведения
![]() выражают через произведение
выражают через произведение
![]() и интеграл от произведения
и интеграл от произведения
![]() .
Естественно, что ее применение оправдано
тогда, когда интеграл, полученный справа,
будет проще заданного.
.
Естественно, что ее применение оправдано
тогда, когда интеграл, полученный справа,
будет проще заданного.
Применение
формулы интегрирования по частям
основывается на следующем: подынтегральное
выражение разбивают на два множителя,
один из которых обозначают через
![]() ,
другой через –
,
другой через –
![]() .
В качестве
.
В качестве
![]() следует брать выражение, от которого
достаточно легко берется интеграл, за
следует брать выражение, от которого
достаточно легко берется интеграл, за
![]() – функцию, которая упрощает выражение.
Таким образом, в эту формулу входят
четыре элемента:
– функцию, которая упрощает выражение.
Таким образом, в эту формулу входят
четыре элемента:
![]() .
.
Например.
1.
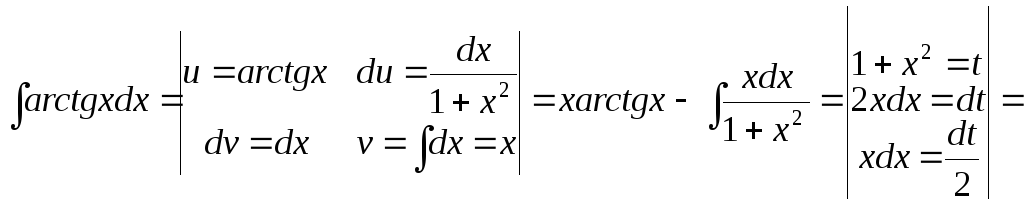
![]() ;
;
2.
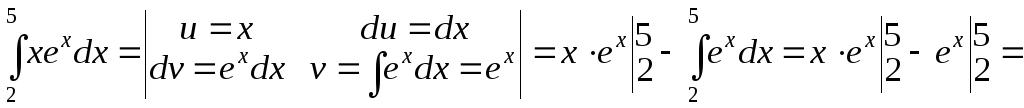
![]() ;
;
Можно указать основные типы интегралов, к которым применима формула интегрирования по частям:
|
|
Здесь
рекомендуется вводить такие обозначения:
|
|
|
Здесь
рекомендуется элементы подынтегрального
выражения обозначать так:
|
|
|
|
Например:
а)
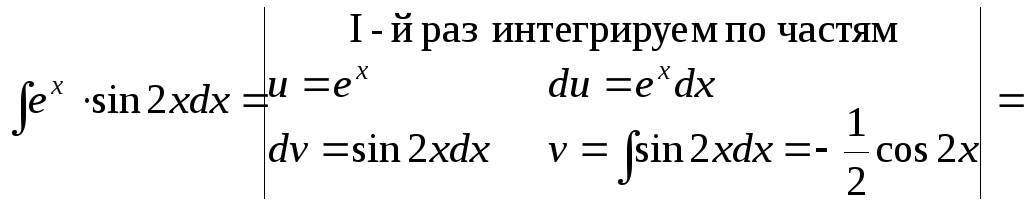
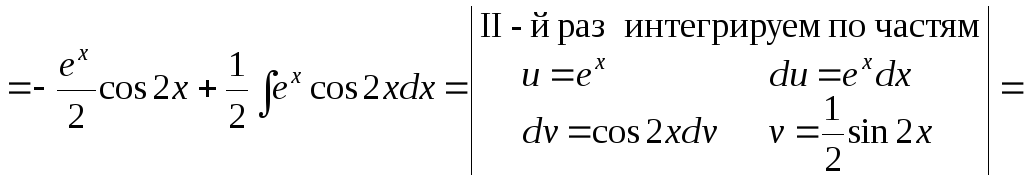
![]() ;
;
Составим равенство для начального и конечного выражений:
![]() .
.
Приведем подобные элементы, собрав их в правой части:
![]() .
.
Теперь легко получить значение искомого интеграла:
![]() .
.
б)
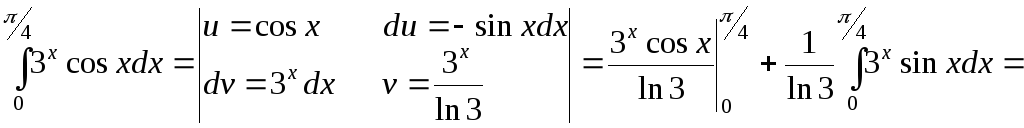
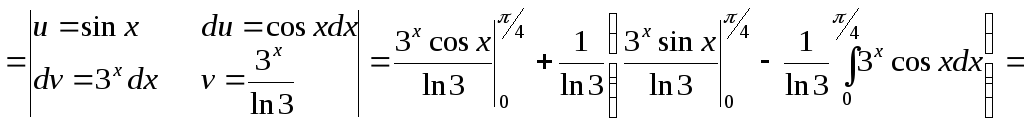
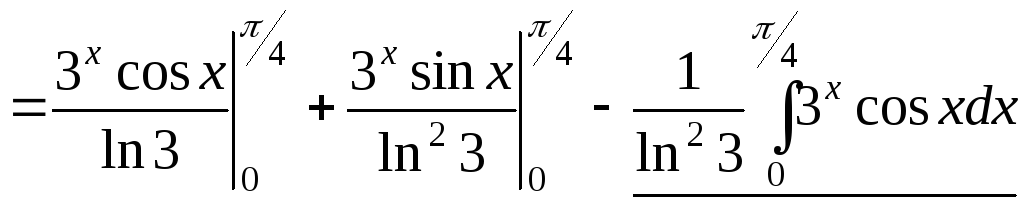 .
.
Объединим начало и конец равенства:
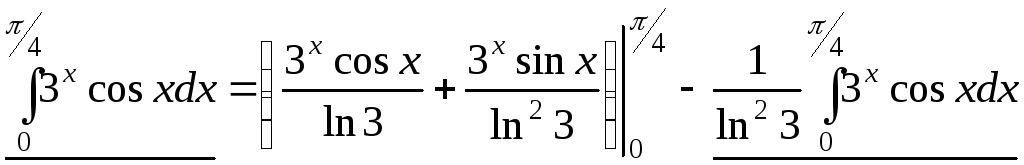 ;
;
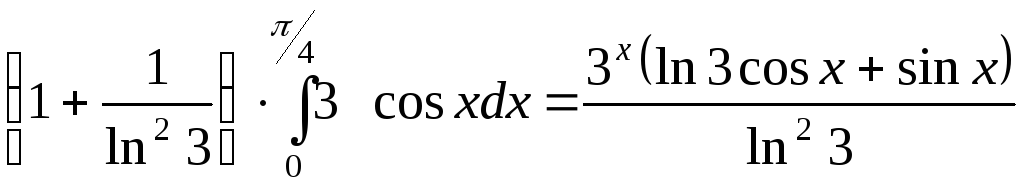 ;
;
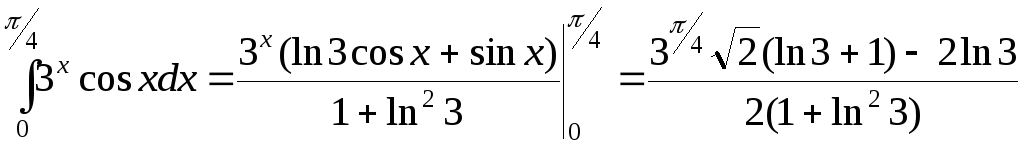 .
.
в)
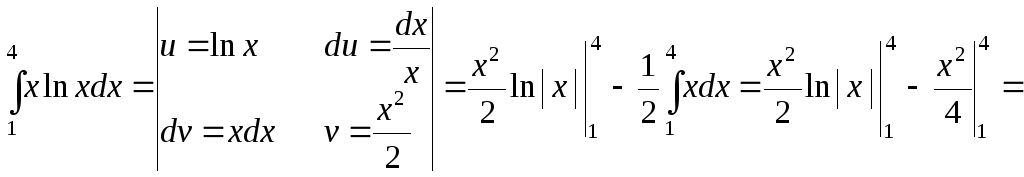
![]() .
.
Замечание. Рассмотренные приемы часто применяют одновременно для нахождения одного интеграла.
Примеры:
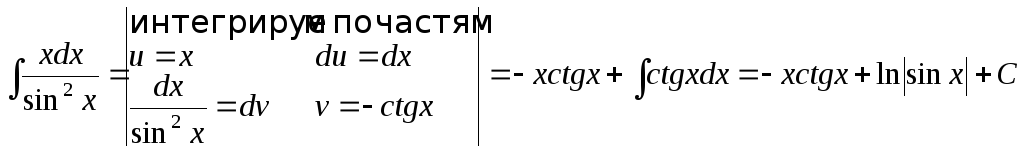 ;
;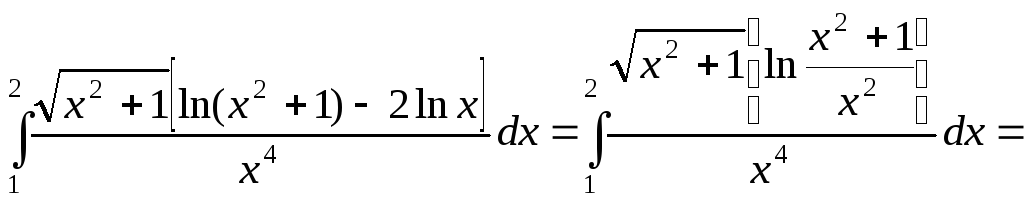
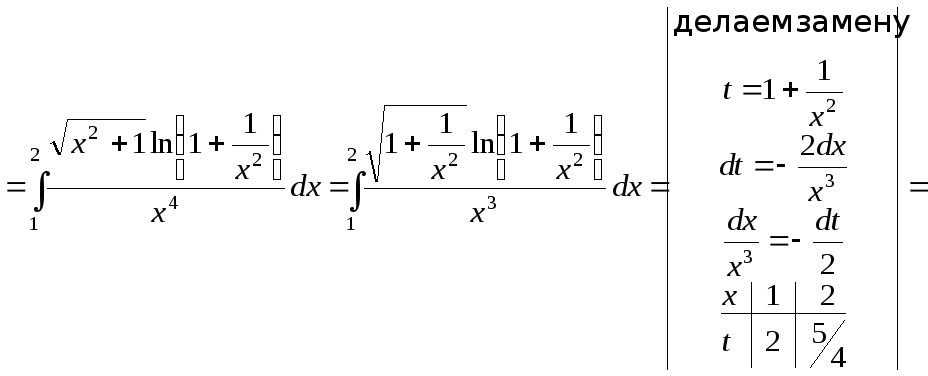
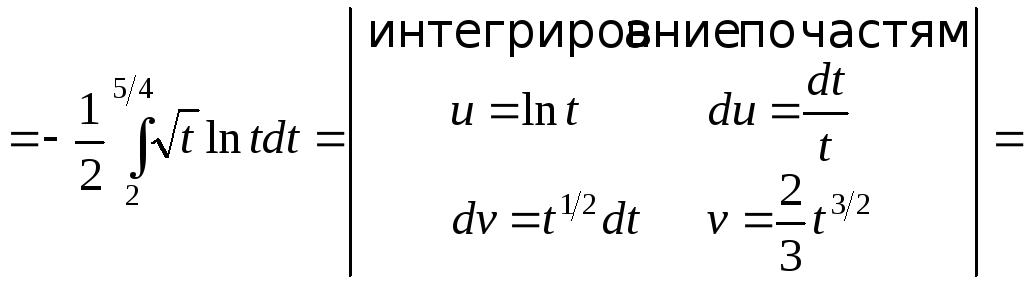
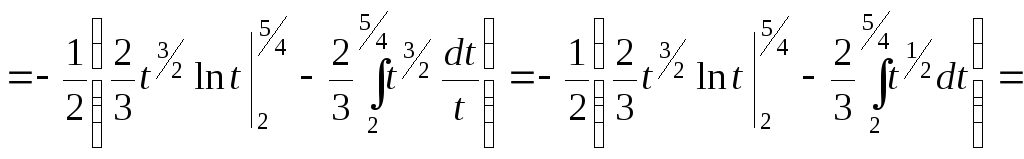
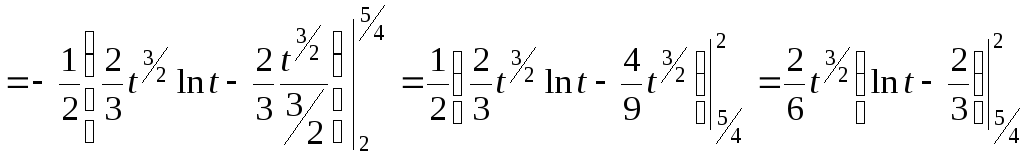
![]() ;
;
3.
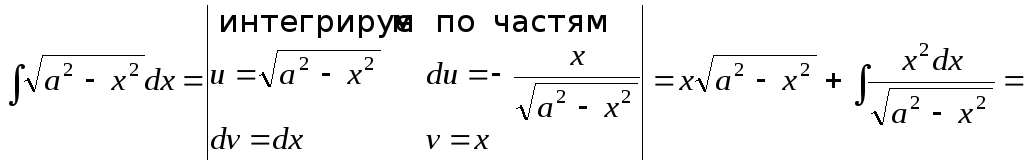
![]()
![]() .
.
![]() ;
;
4.
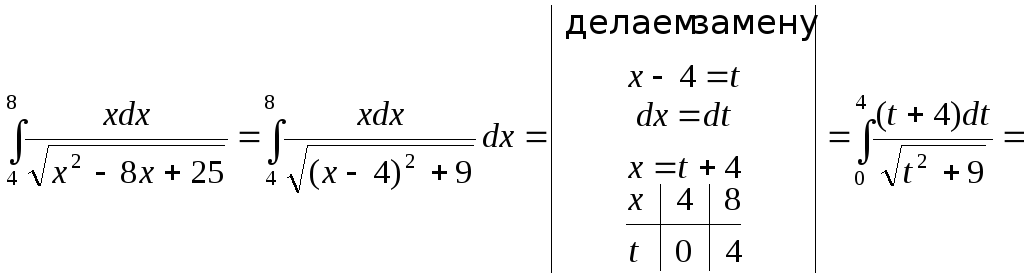
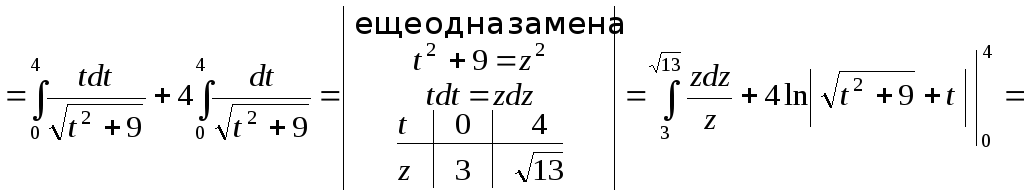
![]() .
.
2.4. Интегрирование рациональных дробей
1. Простые (правильные) дроби бывают четырех типов:
|
|
|
|
![]()
![]() –действительные
числа.
–действительные
числа.
![]() –не
имеет действительных корней и на
множители не раскладывается.
–не
имеет действительных корней и на
множители не раскладывается.
Рассмотрим интегрирование каждой из этих дробей.
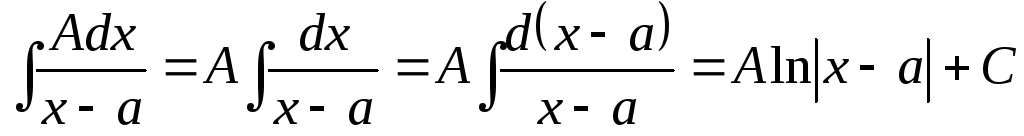 ;
;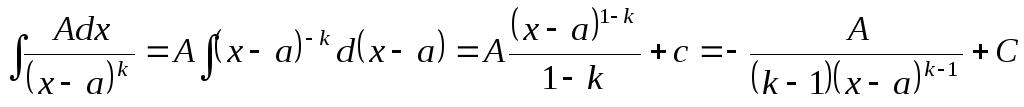 .
.
Например,
![]() .
.
Для интегрирования дробей III типа необходимо опираться на такие интегралы:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
IV.
![]() – вычисление интеграла этого типа
связано с выделением полного квадрата
в знаменателе: заменой переменной;
рассмотрением суммы интегралов типа
а), б).
– вычисление интеграла этого типа
связано с выделением полного квадрата
в знаменателе: заменой переменной;
рассмотрением суммы интегралов типа
а), б).
Например,
а)
![]()
![]() ;
;
б)
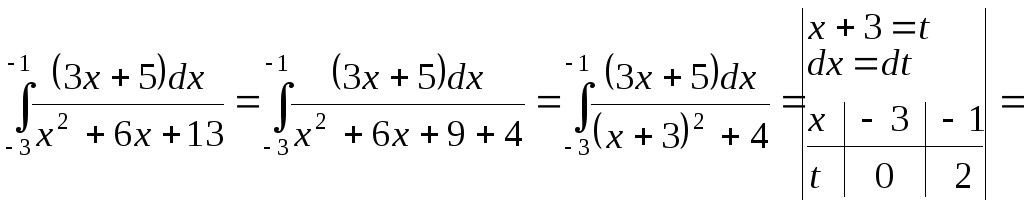
![]()
![]() .
.
в)
![]() .
.
2.
Рассмотрим правильную рациональную
дробь
![]()
(![]() ,
,
![]() – многочлены и степень
– многочлены и степень
![]() меньше степени
меньше степени
![]() ).
).
|
Теорема 5. |
(из алгебры). Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей. |
Нам
необходимо указать способ разложения
такой дроби на простые. Он тесно связан
с разложением знаменателя
![]() на множители. Известно, что каждый целый
многочлен с действительными коэффициентами
может быть разложен единственным образом
на действительные множители типа
на множители. Известно, что каждый целый
многочлен с действительными коэффициентами
может быть разложен единственным образом
на действительные множители типа
![]() и
и
![]() ,
далее неразложимые.
,
далее неразложимые.
Рассмотрим несколько случаев:
а)
![]() ,
тогда дробь представляют в виде:
,
тогда дробь представляют в виде:
![]() ,
,
где
![]() – коэффициенты, которые следует
определить.
– коэффициенты, которые следует
определить.
б)
![]() ,
тогда
,
тогда
![]()
![]() ,
,
![]() –необходимо
определить.
–необходимо
определить.
в)
![]() .
.
![]()
![]() .
.
Последовательность разложения правильной рациональной дроби будет такой:
|
1) |
Знаменатель дроби раскладывают на множители. |
|
2) |
Заданную дробь представляют в виде суммы простых дробей с неизвестными коэффициентами. |
|
3) |
Приводят к общему знаменателю сумму простых дробей и приравнивают числители обеих частей равенства. |
|
4) |
Определяют коэффициенты и переходят к интегрированию простых дробей. |
Покажем все этапы на примерах.
а)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Чтобы
найти значения
![]() используют два способа:
используют два способа:
а)
задают конкретные значения
![]() (корни знаменателя);
(корни знаменателя);
б)
приравнивают коэффициенты при одинаковых
степенях
![]() и решают систему.
и решают систему.
Первый прием особенно удобен, когда знаменатель раскладывается на разные множители. В данном примере его применение позволяет получить такие результаты:
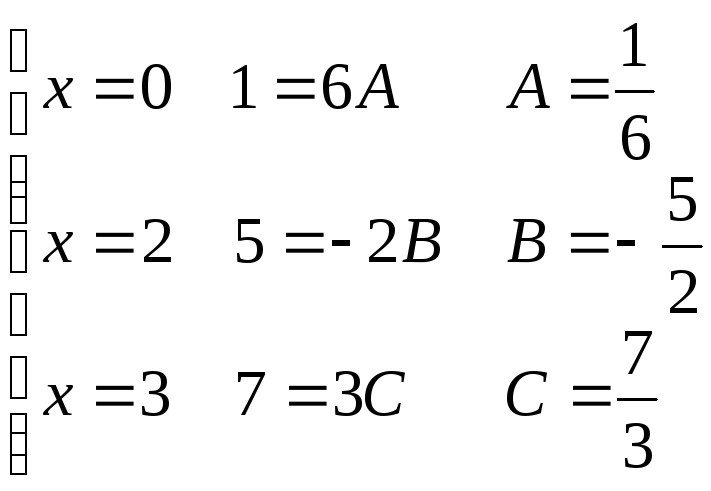 ;
;
![]() ;
;
![]()
![]() .
.
б)
![]() ;
;
![]() ;
;
![]() .
.
Приравняем
коэффициенты при одинаковых степенях
переменной
![]() .
.
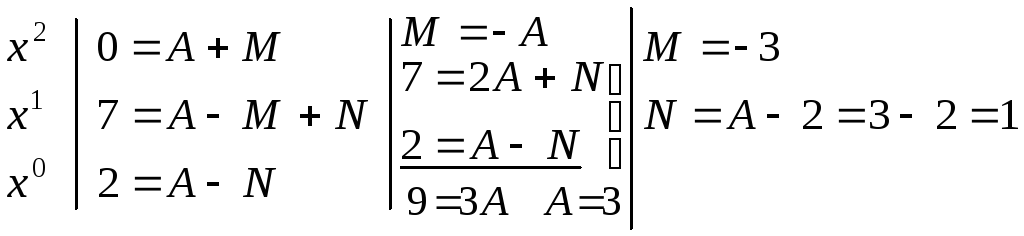 ;
;
![]() .
.
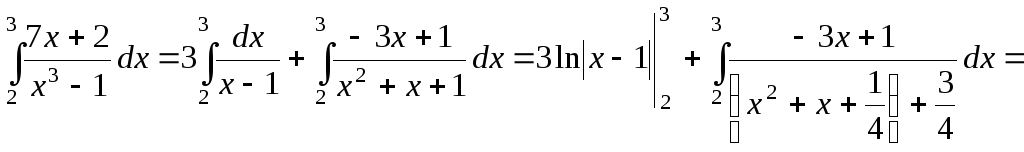
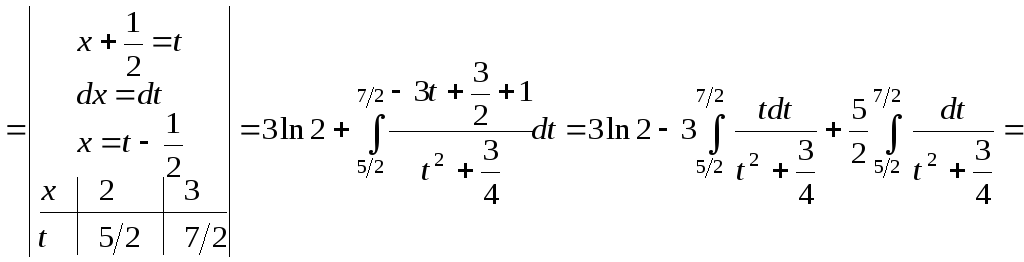
![]()
![]() .
.
3. Рассмотрим дробь четвертого типа.
![]() ;
;
![]()
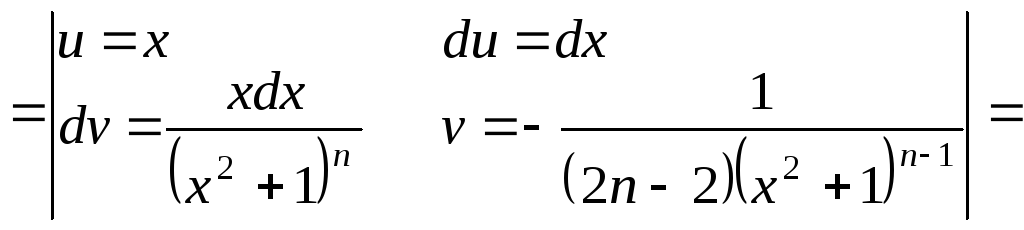
![]() .
.
![]() .
.
|
|
– рекуррентное
соотношение, позволяющее последовательно
упрощать интеграл и свести его до
|
Примеры.
а)
![]()
![]() .
.
б)
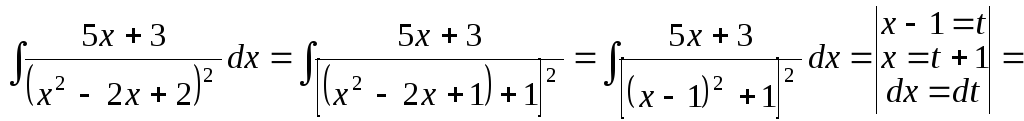
![]()
![]()
![]() .
.
|
Замечание 1. |
Если
при выделении полного квадрата в
качестве “остатка” будет не 1, а другое
число и
|
|
|
|
|
Замечание 2. |
Если подынтегральная дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и правильной дроби. |
Например,
![]() – неправильная дробь.
– неправильная дробь.
Выполним деление, чтобы выделить целую часть:
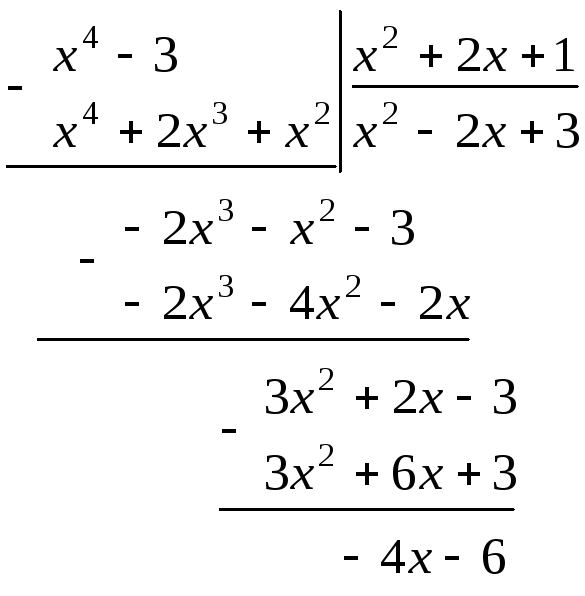
Таким образом, числитель дроби можно представить так:
![]()
![]()
![]()
![]()
![]() .
.