2.5. Несобственные интегралы

2.5.1. Интегралы с бесконечными пределами

Определение интеграла, приведенное в п. 2.1, было дано в предположении, что областью интегрирования является конечный промежуток . Если же предположить, что область интегрирования бесконечна, например, является интервалом, то даже для непрерывной функцииобычное определение интеграла становится неприемлемым. В данном случае нельзя говорить об интегральных суммах, так как при любом разбиении интервалана конечное число частей одна из этих частей будет бесконечной.

Если интеграл стремится к конечному пределу при неограниченном возрастании, то этот предел называютнесобственным интегралом сбесконечной верхней границейот функциии обозначают символом.

Таким образом,

.

В этом случае говорят, что несобственный интеграл существуетилисходится. Если указанный предел не существует (в частности, если он бесконечен), то говорят, что интегралне существуетилирасходится.

Аналогично определяется несобственный интегралс бесконечной нижней границей:

.

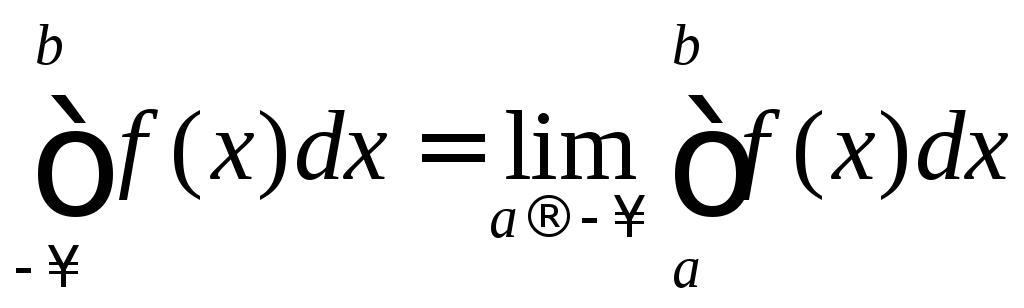Несобственный интегралс двумя бесконечными границамиопределяется формулой

,

где – любая фиксированная точка оси.

Таким образом, интеграл 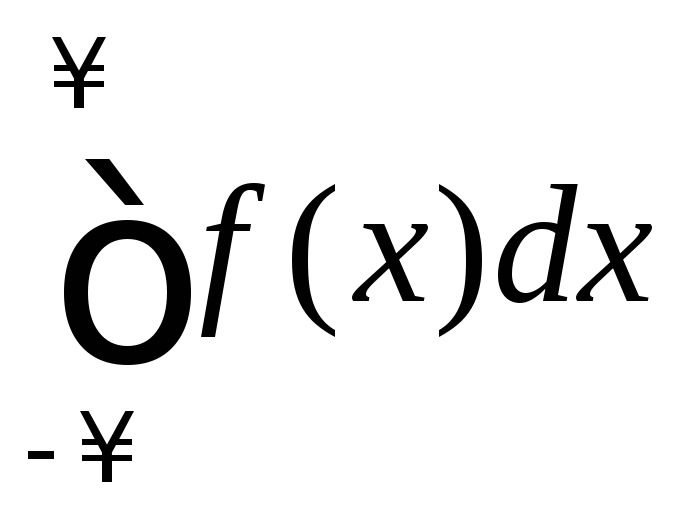существует тогда и только тогда, когда существует каждый из интегралови.

2.5.2. Интегралы от непрерывных функций

а) Пусть непрерывна во всех точках отрезказа исключением точки , где, тогда:

.

б) Пусть непрерывна во всех точках отрезказа исключением точки , тогда:

.

в) Пусть непрерывна во всех точках отрезказа исключением точки , тогда:

.

г) Пусть непрерывна во всех точках отрезказа исключением точек и , тогда:

.

Эти интегралы могут как сходиться, так и расходиться.

Пример 2.5.1.Исследовать интеграл на сходимость.

Решение.

–интеграл сходится.

Пример 2.5.2.Исследовать интеграл на сходимость.

Решение.

–интеграл расходится.

Пример 2.5.3.Исследовать интеграл на сходимость.

Решение.

–сходится.

Пример 2.5.4.Исследовать интеграл на сходимость.

Решение.

–расходится.

Пример 2.5.5.Исследовать интеграл на сходимость.

Решение.

.

Пример 2.5.6.Исследовать интеграл на сходимость.

Решение.

–интеграл расходится.

Пример 2.5.7.Исследовать интеграл на сходимость.

Решение.

–интеграл расходится.

Пример 2.5.8.Исследовать интеграл на сходимость.

Решение.

–расходится.

Пример 2.5.9.Исследовать интеграл на сходимость.

Решение.

–сходится.

Пример 2.5.10.Исследовать интеграл на сходимость.

Решение.

–интеграл расходится.

Пример 2.5.11.Исследовать интеграл на сходимость.

Решение.

–интеграл сходится.

35