2. Определенный интеграл

1. Определенный интеграл как предел интегральной суммы

Пусть функция определена на отрезке. Этот отрезок разделим напроизвольных частей (рис.1). Обозначим абсциссы точек деления через

.

В каждом частичном промежутке возьмем произвольную точку. Умножив значение функции в точкена длину соответствующего частичного промежутка, получим

.

Составим сумму

,

рис.1

которую называют интегральной суммой функции отрезка, и перейдем к пределу

,

(1)

где – наибольшая из разностей.

Если существует конечный предел (1), то он называется определенным интегралом в промежутке отдои обозначается

,

где число называютверхним пределом,

число называютнижним пределом,

–подынтегральной функцией,

–подынтегральным выражением,

–переменной интегрирования.

2. Простейшие свойства определенного интеграла.

Формула Ньютона-Лейбница

I. Интеграл с одинаковыми пределами интегрирования равен нулю: .

II. Если в интеграле поменять местами пределы интегрирования, то интеграл изменит знак: .

III. Если функцияинтегрируема на отрезке, то она интегрируема на любом отрезке, содержащемся в: , .

IV. Постоянный множитель можно выносить за знак интеграла: .

V. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций: .

Рассмотрим формулу Ньютона-Лейбница.Если функциянепрерывна на промежутке, то

,

(2)

где – первообразная функция для, т.е..

Пример 2.2.1.Вычислить интеграл.

Решение.

.

Пример 2.2.2.Вычислить интеграл.

Решение..

Пример 2.2.3.Вычислить интеграл.

Решение.Выделим полный квадрат в знаменателе дроби.

.

Пример 2.2.4.Вычислить интеграл.

Решение..

2.3. Замена переменной в определенном интеграле

Если функция непрерывна в промежуткеи функциянепрерывна вместе со своей производнойв промежутке, причем,и при изменениив промежутке, значенияне выходят за пределы промежутка непрерывности функции, то

.

Пример 2.3.1.Вычислить интеграл.

Решение.Данный интеграл легко приводится к интегралу вида, поэтому применим подстановку,. Определим новый промежуток интегрирования: если, тои; если, тои, следовательно,

.

Пример 2.3.2.Вычислить интеграл.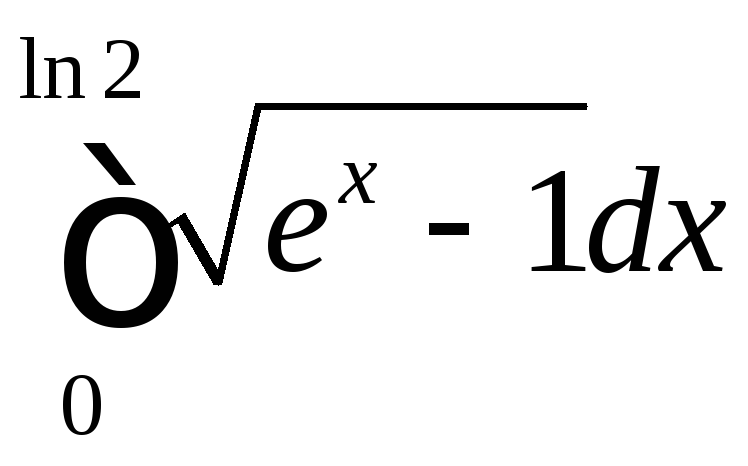

Решение.Применим подстановку,,,. Если, то; если, то, следовательно,

.

Пример 2.3.3.Вычислить интеграл.

Решение.Применим подстановку,,или. Если, то; если, то, следовательно,

.

2.4. Интегрирование по частям в определенном интеграле

Если функции инепрерывны вместе со своими производнымиив промежутке, то имеет место следующая формула интегрирования по частям:

.

Пример 2.4.1.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

Пример 2.4.2.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

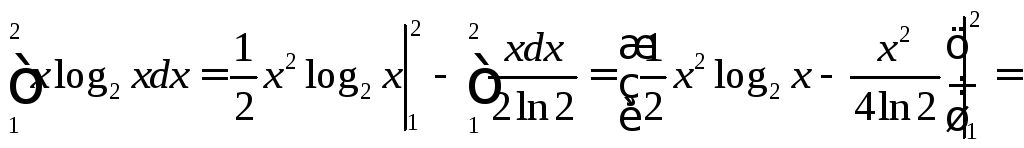
Пример 2.4.3.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

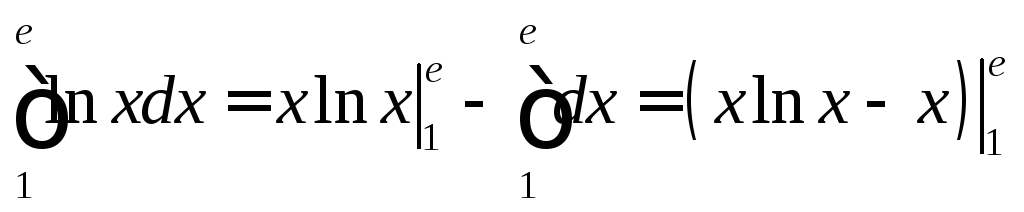Интеграл вычисляем методом интегрирования по частям. Пусть,, тогда,и. Окончательно получим

.