1.6. Интегрирование по частям

Формула интегрирования по частям имеет вид

,

где и – дифференцируемые функции.

Применение формулы интегрирования по частям основывается на следующем:

подынтегральное выражение разбивают на два множителя, один из которых обозначают через , другой через –. В качествеследует брать выражение, от которого достаточно легко берется интеграл, за– функцию, которая упрощает выражение. Затем по установленному выражениюдифференцированием найти, а по известномупутем интегрирования найти функцию(при этом считают, что).

Для интегралов вида , где- многочлен, заследует принять.

Для интегралов вида ,,запринимаются соответственно функции,,,,,.

Для интегралов вида заможно принять любую из функций, но здесь требуется двукратное интегрирование по частям.

Пример 1.6.1.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

Пример 1.6.2.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

(а)

Теперь найдем интеграл в правой части равенства (а) с помощью подстановки . Дифференцируя, получаемили, следовательно,

.

Подставляя этот результат в равенство (а), находим

.

Пример 1.6.3.Вычислить интеграл.

Решение.Данный интеграл представляет собой произведение обратной тригонометрической функции на многочлен нулевой степени. Тогда, для интегрирования по частям, полагая,, имеем,, следовательно,

.

(б)

Интеграл в правой части найдем с помощью подстановки ,;

.

Подставляя этот результат в равенство (б), получаем

.

Пример 1.6.4.Вычислить интеграл.

Решение.Для интегрирования по частям, полагая,, имеем,, следовательно,

.

(в)

Интеграл в правой части снова интегрируем по частям. Полагая ,, имеем,, следовательно,

.

Подставляя этот результат в равенство (в), получаем

,

приведем подобные элементы

.

Следовательно,

.

Пример 1.6.5.Вычислить интеграл.

Решение.Для интегрирования по частям, полагая,, имеем,, следовательно,

.

(г)

Интеграл в правой части снова интегрируем по частям. Полагая ,, имеем,, следовательно,

.

Подставляя этот результат в равенство (г), получаем

.

Пример 1.6.6.Вычислить интеграл.

Решение.Полагая,, имеем,, следовательно,

.

(д)

Вычисляем интеграл в правой части равенства (д) с помощью формулы интегрирования по частям: ,,,, следовательно,

.

Подставляя этот результат в равенство (д), получаем

.

1.7. Интегрирование некоторых выражений, содержащих квадратный трехчлен

Для вычисления интегралов вида

; ;,

содержащих квадратный трехчлен, применяют прием выделения полного квадрата из квадратного трехчлена. После этого применяют уже известные методы интегрирования.

Пример 1.7.1.Вычислить интеграл.

Решение.Преобразуем знаменатель, выделив полный квадрат из квадратного трехчлена:.

.

Пример 1.7.2.Вычислить интеграл.

Решение.Преобразуем знаменатель, выделив полный квадрат из квадратного трехчлена:.

.

Пример 1.7.3.Вычислить интеграл.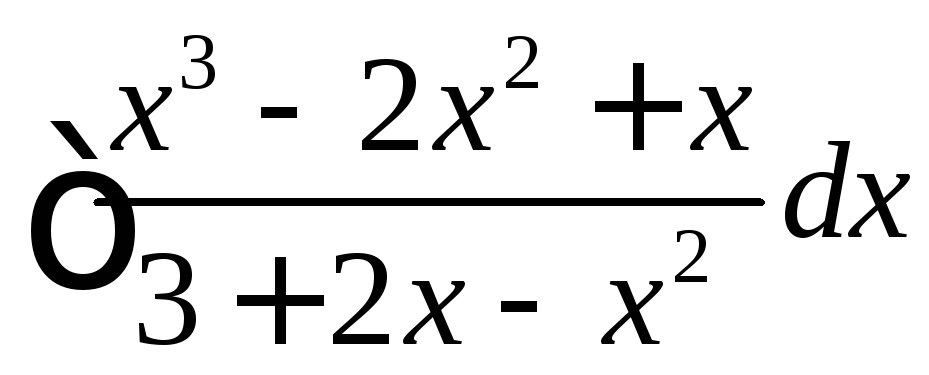

Решение.Подынтегральная рациональная дробь неправильная. Разделим числитель на знаменатель и представим данную дробь в виде суммы целой рациональной функции и правильной рациональной дроби:

Получим

.

В знаменателе подынтегрального выражения выделим полный квадрат .

.

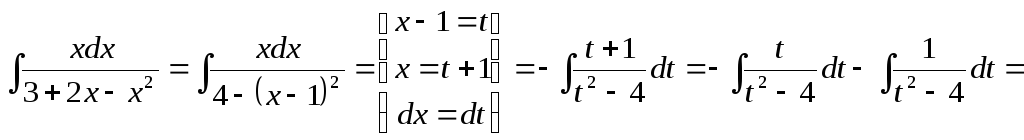
Следовательно, .

Пример 1.7.4.Вычислить интеграл.

Решение.В знаменателе подынтегрального выражения выделим полный квадрат.

.

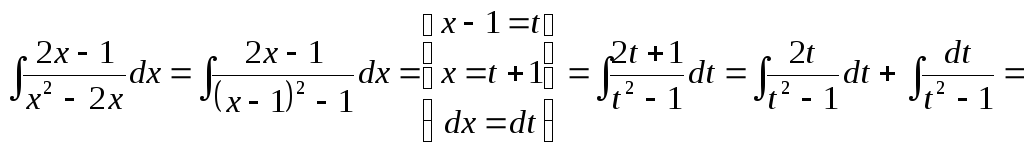
Пример 1.7.5.Вычислить интеграл.

Решение.В знаменателе подынтегрального выражения выделим полный квадрат

.

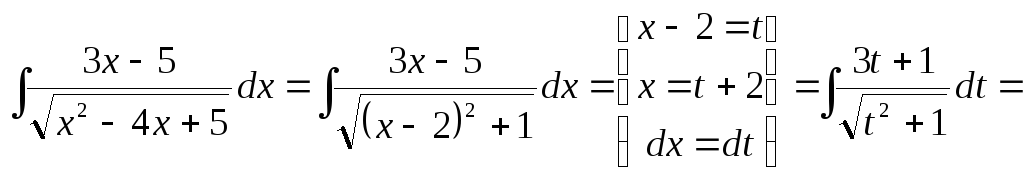
Пример 1.7.6.Вычислить интеграл.

Решение.В знаменателе подынтегрального выражения выделим полный квадрат

.

Замечание. Интегралв зависимости от знака коэффициенталегко свести к интеграламили, каждый из которых можно вычислить методом интегрирования по частям.

Пример 1.7.7.Вычислить интеграл.

Решение..

.

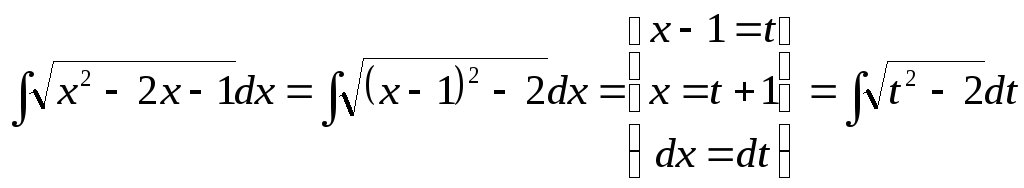Последний интеграл вычислим методом интегрирования по частям. Полагая ,. Имеем,, следовательно,

,

откуда

или

.

Учитывая, что , получаем

.