1.3. Таблица основных интегралов

	(1)
	(2)
	(3)
	(4)
	(5)
	(6)
	(7)
	(8)
	(9)
	(10)
	(11)
	(12)
	(13)
	(14)
	(15)

Справедливость формул можно проверить путем дифференцирования, т.е. надо убедиться в том, что производные от правых частей формул будут равны соответственно подынтегральным функциям. Так, если , то.

Например, в формуле (14) ;;

, т.е. .

Аналогичным способом можно проверить и все остальные формулы. Заметим, что каждая из формул таблицы справедлива в любом промежутке, содержащемся в области определения подынтегральной функции.

Интегралы таблицы называются табличными.

4. Непосредственное интегрирование

Пользуясь таблицей интегралов и свойствами I, II неопределенного интеграла, можно вычислить многие интегралы.

Пример 1.4.1.Вычислить интеграл.

Решение.. Воспользовались формулой (3).

Пример 1.4.2.Вычислить интеграл.

Решение.

. Воспользовались формулой (3).

Пример 1.4.3.Вычислить интеграл.

Решение.

. Воспользовались свойством IIи формулами (1), (3).

Пример 1.4.4.Вычислить интеграл.

Решение.

. Воспользовались свойством IIи формулами (1), (3), (2), (4).

Пример 1.4.5.Вычислить интеграл.

Решение.

Воспользовались свойствами IIиIи формулами (2), (4).

Пример 1.4.6.Вычислить интеграл.

Решение.Подынтегральная функция является неправильной дробью, т.к. степень числителя больше степени знаменателя. Разделив числитель на знаменатель, получим

. Воспользовались свойствами IIиIи формулами (3), (2), (12).

Пример 1.4.7.Вычислить интеграл.

Решение.. Воспользовались формулой (5).

Пример 1.4.8.Вычислить интеграл.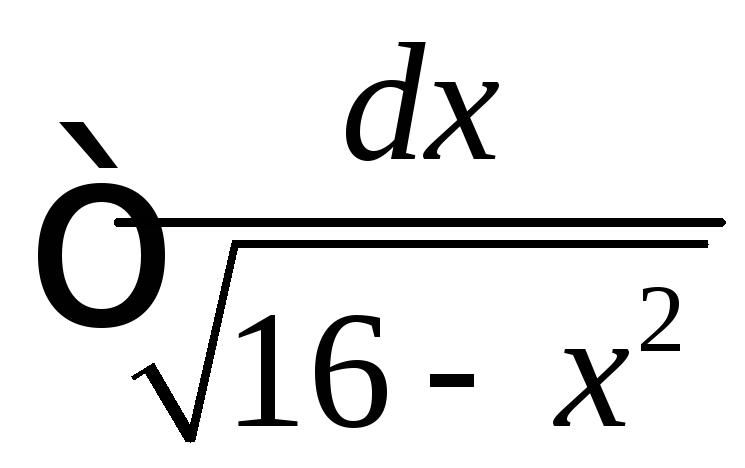

Решение.. Воспользовались формулой (11).

Пример 1.4.9.Вычислить интеграл.

Решение.. Воспользовались формулой (13).

Пример 1.4.10.Вычислить интеграл.

Решение.. Воспользовались формулой (14).

Пример 1.4.11.Вычислить интеграл.

Решение.

. Воспользовались формулой (12).

Пример 1.4.12.Вычислить интеграл.

Решение.. Воспользовались формулой (11).

Пример 1.4.13.Вычислить интеграл.

Решение.. Воспользовались формулой (14).

Пример 1.4.14.Вычислить интеграл.

Решение.. Воспользовались формулой (13).

Пример 1.4.15.Вычислить интеграл.

Решение.. Воспользовались свойствамиIIиIи формулами (2), (8).

Пример 1.4.16.Вычислить интеграл.

Решение.. Воспользовались свойствомIIи формулами (10), (2).

1.5. Метод подстановки (замена переменной)

1. Пусть функция непрерывная. Полагая,, где производнаяесть функция непрерывная, получаем

.

Если окажется, что интеграл в правой части равенства находится проще исходного, то цель замены переменной достигнута.

Для получения искомого результата в найденном интеграле с новой переменной переходим к переменной, пользуясь исходной формулой.

2. Полезно запомнить частный случай:

.

Интеграл дроби, числитель которой есть дифференциал знаменателя, равен натуральному логарифму модуля знаменателя.

Действительно, положим , тогда. Получим

.

Пример 1.5.1.Вычислить интеграл.

Решение.Наличие множителядает возможность применить подстановку, откуда. Дифференцируя, получаем, следовательно,

.

Пример 1.5.2.Вычислить интеграл.

Решение. Полагаем, , тогда, следовательно,

.

Пример 1.5.3.Вычислить интеграл.

Решение.Полагая, имеем, следовательно,

.

Пример 1.5.4.Вычислить интеграл.

Решение.Множительпозволяет применить подстановку. Имеем, следовательно,

.

Пример 1.5.5.Вычислить интеграл.

Решение.Положим, тогда, следовательно,

.

Или:

.

Пример 1.5.6.Вычислить интеграл.

Решение.Полагая, имеем, следовательно,

.

Или:

.

Проверка.Убедимся, что. Находим

,

следовательно, интегрирование произведено правильно.

Пример 1.5.7.Вычислить интеграл.

Решение..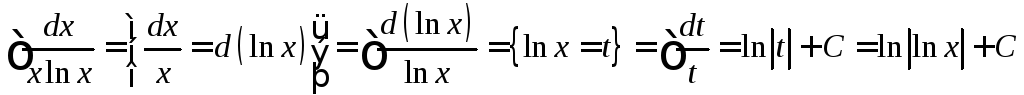

Проверка.Убедимся, что. Находим

,

следовательно, интегрирование произведено правильно.

Пример 1.5.8.Вычислить интеграл.

Решение.

.

Пример 1.5.9.Вычислить интеграл.

Решение.Применим подстановку, тогда;

.

Пример 1.5.10.Вычислить интеграл.

Решение..

Проверка..

Пример 1.5.11.Вычислить интеграл.

Решение.Числитель дроби равен дифференциалу знаменателя, следовательно, интеграл равен логарифму модуля знаменателя

.

Проверка..

Пример 1.5.12.Вычислить интеграл.

Решение..

Пример 1.5.13.Вычислить интеграл.

Решение..

Пример 1.5.14.Вычислить интеграл.

Замечание.Выражения, содержащиеили, можно интегрировать с помощью тригонометрических подстановок. Так, если в подынтегральном выражении содержится, то применяется подстановкаили, если содержится, то подстановкаили, если же содержится, то подстановкаили.

Решение.Применим подстановку, тогда.

.