Дисциплина

ВЫСШАЯ МАТЕМАТИКА

Неопределенный, определенный, несобственный интегралы

I.	Неопределенный интеграл………………….………..……..………
1.1.	Первообразная функция и неопределенный интеграл………………
1.2.	Простейшие свойства неопределенного интеграла……….…….....
1.3.	Таблица основных интегралов…………………………………….....
1.4.	Непосредственное интегрирование……………………………...…..
1.5.	Метод подстановки (замена переменной)………………..…………
1.6.	Интегрирование по частям…………………………………..………
1.7.	Интегрирование некоторых выражений, содержащих квадратный трехчлен……………………………..
1.8.	Интегрирование рациональных функций…………………………….
1.9.	Интегрирование некоторых иррациональных функций……………
1.10.	Интегрирование тригонометрических функций……………………
II.	Определенный интеграл……………….....………………………....
2.1.	Определенный интеграл как предел интегральной суммы…………………...………………………………………………
2.2.	Простейшие свойства определенного интеграла. Формула Ньютона-Лейбница…………………………………………………...
2.3.	Замена переменной в определенном интеграле..…………………….
2.4.	Интегрирование по частямв определенном интеграле………..……………………………………………………..
2.5.	Несобственные интегралы…………………………………………..

1. Неопределенный интеграл

1. Первообразная функция и неопределенный интеграл

В дифференциальном исчислении одной из основных задач является нахождение производной или дифференциала от данной функции :

или

.

В интегральном исчислении основной является обратная задача – отыскание функции по заданной ее производнойили дифференциалу, т.е. для данной функциинадо найти такую функцию, что

или

.

Функция , производная которой равна, а дифференциалназываетсяпервообразной функциейдля функции.

Приведем примеры.

1) Если , то первообразная будет, так как.

2) Если , то, так как.

Заметим, что если – первообразная функция для функции, то и(–произвольная постоянная) есть также первообразная функция, так как

.

Например, пусть , тогдабудет первообразной функцией для данной функции, так как

.

Общее выражение совокупности всех первообразных функций для данной непрерывной функцииназываетсянеопределенным интегралом от функциии обозначается символом, где. Функцияназываетсяподынтегральной функцией,–подынтегральным выражением.

Задача состоит в нахождении хотя бы одной первообразной, что достигается путем интегрирования. При этом следует иметь в виду, что правильность интегрирования проверяется дифференцированием.

2. Простейшие свойства неопределенного интеграла

1. Постоянный множитель 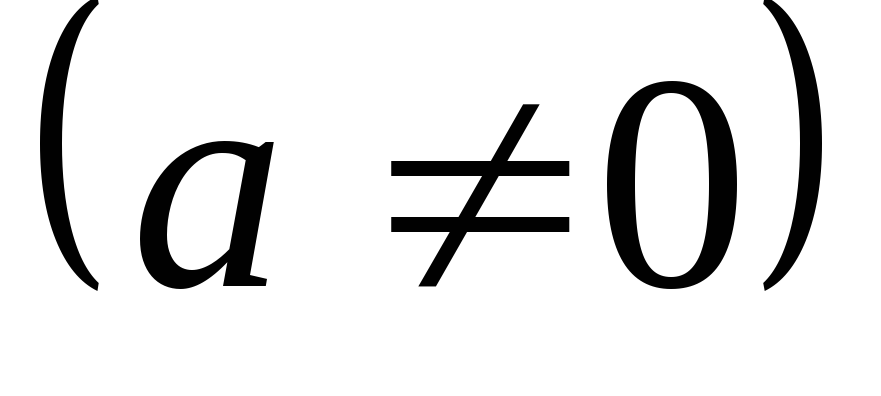можно выносить за знак интеграла:

.

2. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций:

.

3. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению

или .

4. Неопределенный интеграл от дифференциала функции равен сумме этой функции и произвольной , т.е.

или .

V. Если справедливо равенство, то справедливым будет и соотношение:

.