
- •Практические занятия по геометрии
- •1 Семестр
- •Раздел 1. Элементы векторной алгебры в пространстве
- •Тема 1.1.Направленные отрезки. Векторы.
- •Тема 1.2.Умножение векторов на действительные числа
- •Тема 1.3.Коллинеарные и компланарные векторы.
- •Тема 1.4.Скалярное произведение векторов
- •Тема 1.5.Векторные подпространства
- •Тема 1.6.Применение векторов к решению задач
- •Задачи повышенной трудности
- •Домашнее задание
- •Индивидуальные задания по векторной алгебре Вариант I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
Тема 1.5.Векторные подпространства
Литература: [1], § 9, стр. 28-32.
Основные определения, теоремы и формулы
Пусть L – непустое множество векторов из векторного пространства V. Множество называется векторным подпространством пространства V, если выполнены следующие два условия.
Если
 и
и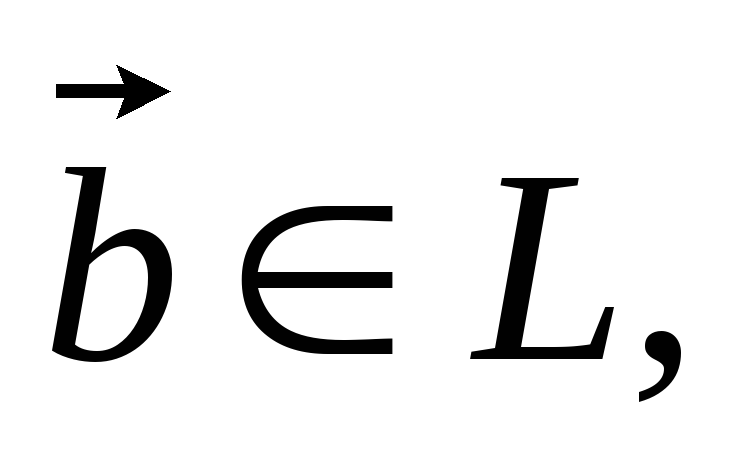 то
то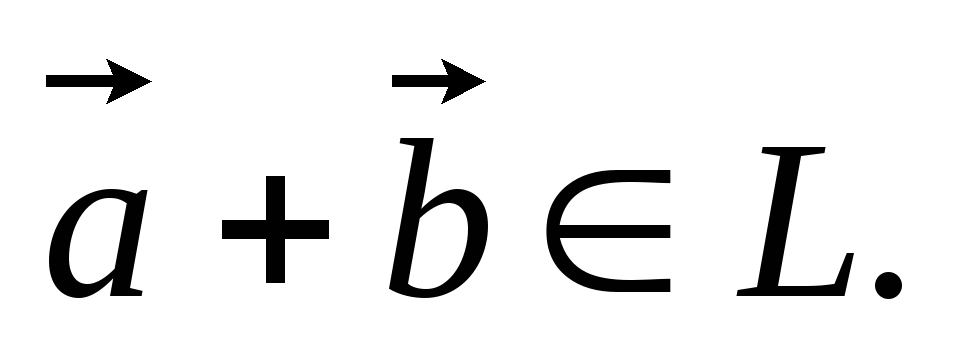
Если
 ,
то
,
то для любого вещественного числа
для любого вещественного числа .
.
Например, множество векторов, параллельных фиксированной плоскости образует подпространство векторного пространства. Так как при сложении двух векторов, параллельных плоскости, снова получим вектор, параллельный той же плоскости и при умножении вектора, параллельного фиксированной плоскости, так же получим вектор, параллельный этой плоскости.
Вопросы для самоконтроля
1. Что такое размерность подпространства? Поясните ответ на примерах.
2. Приведите примеры: 1) нульмерного; 2) одномерного; 3) двумерного подпространства.
3. Приведите примеры базисов в одномерном и двумерном пространствах.
4. Что такое координаты вектора в двумерном векторном пространстве? Почему у любого вектора двумерного пространства координаты относительно фиксированного базиса всегда существуют и определяются единственным образом?
5. Перечислите свойства координат векторов в двумерном подпространстве.
6. Доказать, что пересечение любых двух векторных подпространств всегда не пусто.
7. Является ли векторным подпространством пересечение (объединение) двух векторных подпространств?
Задачи
Являются ли векторным подпространством каждая из следующих совокупностей векторов: а) все векторы трехмерного векторного пространства, координаты которых – целые числа? б) все векторы трехмерного векторного пространства, не параллельные данной прямой? в) все векторы трехмерного векторного пространства, координаты которых имеют вид (1,a,b), где a,b – действительные числа? г) все векторы (x,y,z) трехмерного векторного пространства, координаты которых удовлетворяют уравнению x+y+z=0?
Пусть F – множество всех векторов
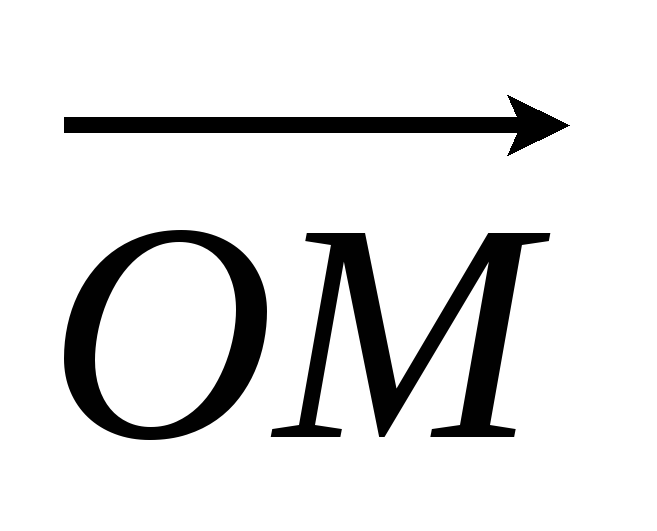 ,
где M
– внутренняя точка данного угла AOB.
Является ли F
векторным пространством?
,
где M
– внутренняя точка данного угла AOB.
Является ли F
векторным пространством?В трехмерном векторном пространстве V3 даны два двумерных векторных подпространства: V2 – натянутое на векторы
 и
и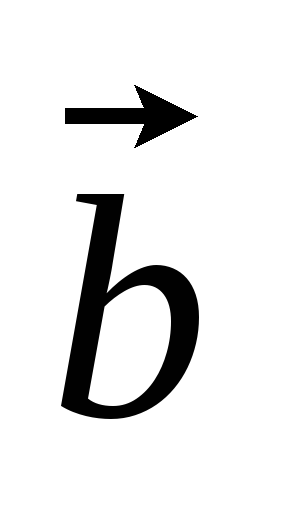 и V2´
– натянутое на векторы
и V2´
– натянутое на векторы
 и
и .
Может ли пересечение V2
и V2´
быть подпространством: а) нульмерным,
б) одномерным, в) двумерным?
.
Может ли пересечение V2
и V2´
быть подпространством: а) нульмерным,
б) одномерным, в) двумерным?В данном базисе (
 ,
, )
построить вектор: а)
)
построить вектор: а) (-2,3),
б)
(-2,3),
б)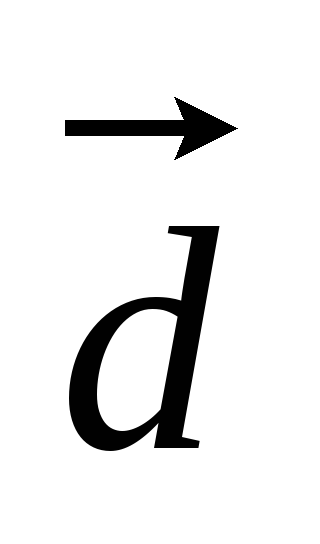 (
( ,
-2).
,
-2).Даны векторы
 (2,3),
(2,3), (1,-3),
(1,-3), (-1,3).
При каком значении коэффициента
(-1,3).
При каком значении коэффициента векторы
векторы =
= +
+
 и
и =-3
=-3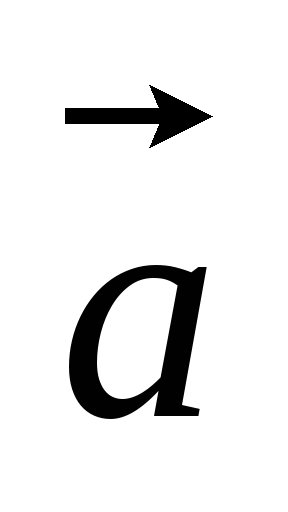 +6
+6 коллинеарны?
коллинеарны?Вектор
 в базисе (
в базисе (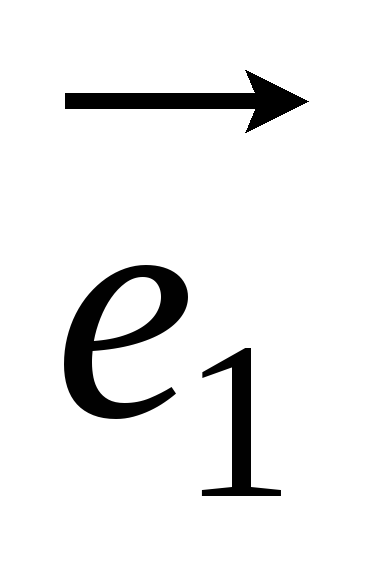 ,
,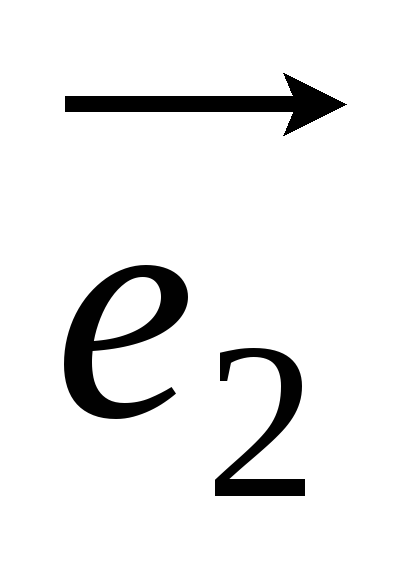 )
имеет координаты (2,1). Доказать, что
векторы
)
имеет координаты (2,1). Доказать, что
векторы =3
=3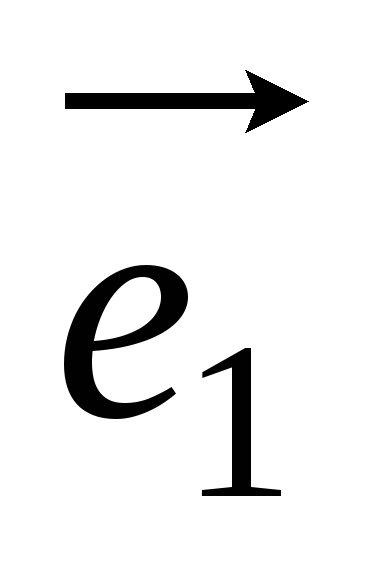 -
- и
и =-2
=-2 +
+ образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора в новом базисе.
в новом базисе.На прямой AB дана точка C такая, что
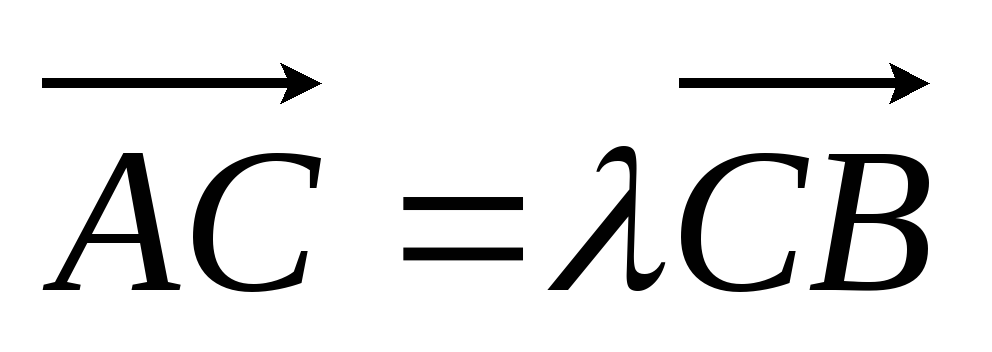 (
(
 -1),
и дана точкаD,
не лежащая на прямой AB.
Разложить: а)
-1),
и дана точкаD,
не лежащая на прямой AB.
Разложить: а)
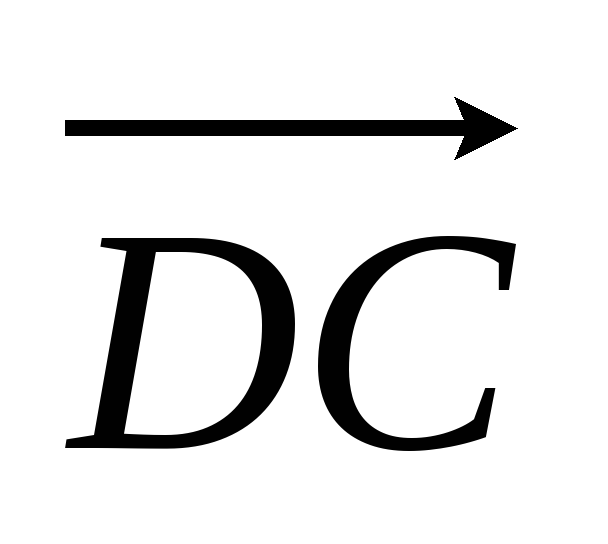 по векторам
по векторам
 и
и
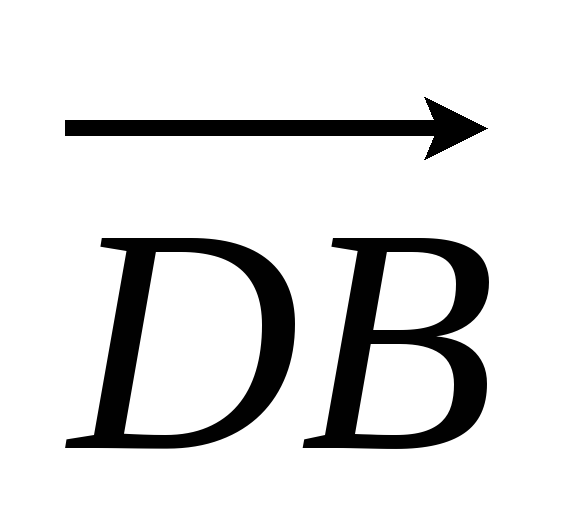 ;
б)
;
б) по
по
 и
и
 ;
в)
;
в)
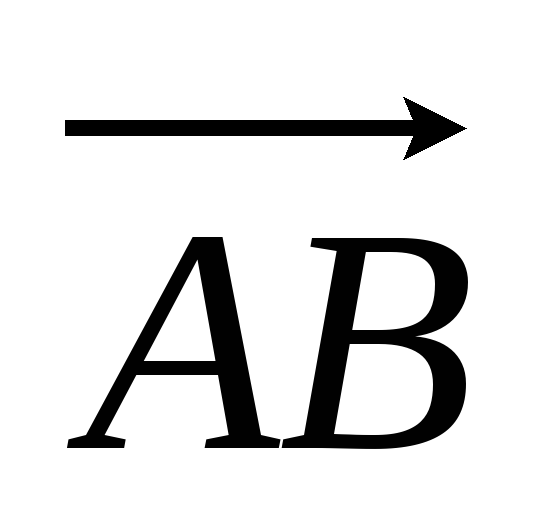 по
по
 и
и
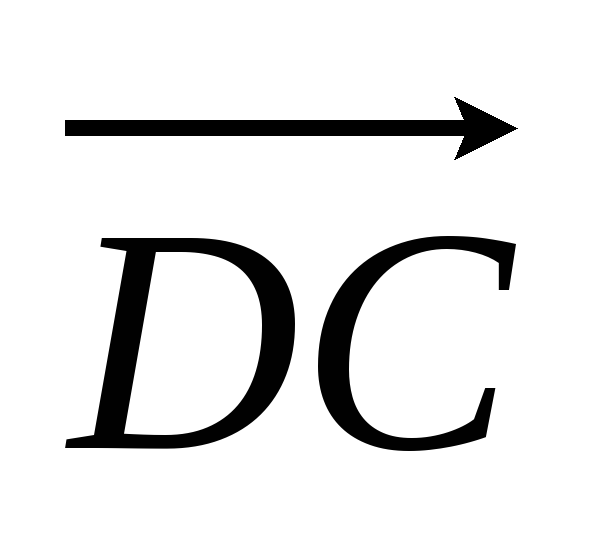 .
.Дан треугольник ABC. Через векторы
 =
= и
и =
=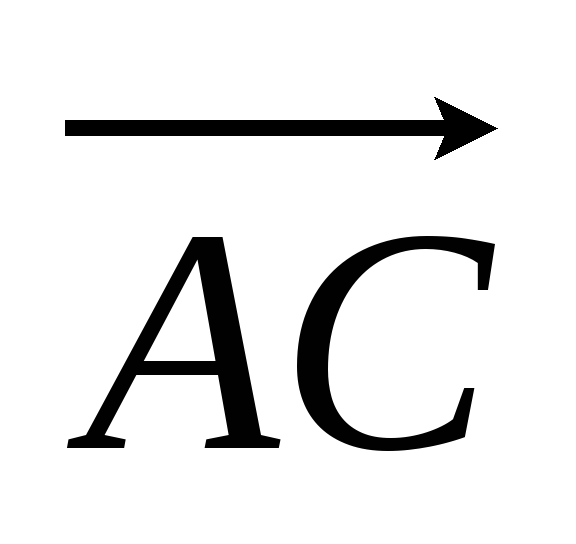 выразить условие того, что M – внутренняя
точка треугольникаABC.
выразить условие того, что M – внутренняя
точка треугольникаABC.
Задачи повышенной трудности
Пусть
V
и F
– два подпространства трехмерного
векторного пространства. Докажите, что:
а) сумма V+F,
то есть множество всех векторов,
представимых в виде суммы вектора из V
и вектора из F,
является векторным подпространством,
б) сумма размерностей подпространств
V+F
и V![]() F
равна сумме размерностей подпространств
V
и F.
F
равна сумме размерностей подпространств
V
и F.
Домашнее задание
Найти координаты вектора
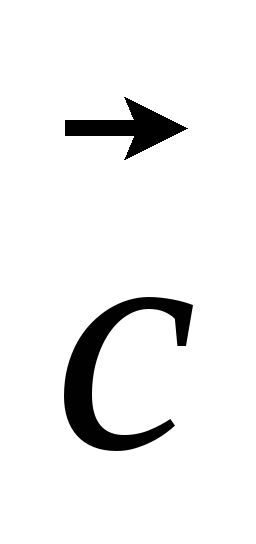 в базисе (
в базисе ( ,
, ),
если: а)
),
если: а)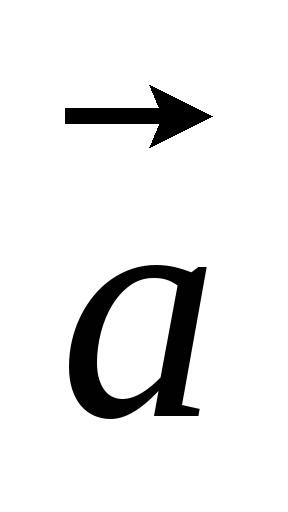 (4,-2),
(4,-2), (1,3),
(1,3),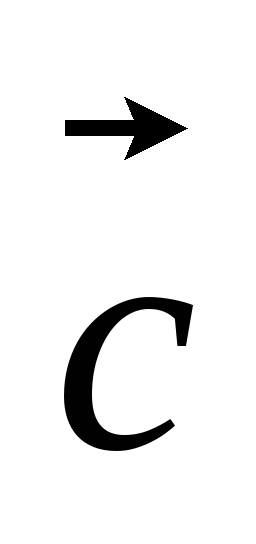 (2,-5);
б)
(2,-5);
б)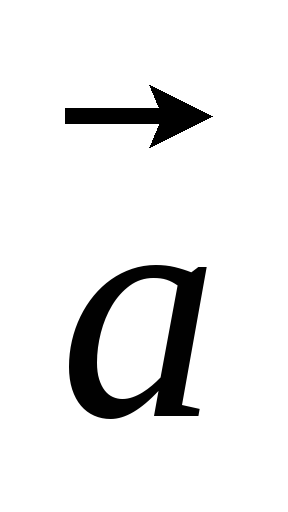 (5,2),
(5,2), (-1,3),
(-1,3), (12,-5).
(12,-5).Дан параллелограмм ABCD. Через векторы
 =
= и
и =
= выразить условие того, чтоM
- внутренняя точка параллелограмм ABCD.
выразить условие того, чтоM
- внутренняя точка параллелограмм ABCD.Могут ли для тройки компланарных векторов
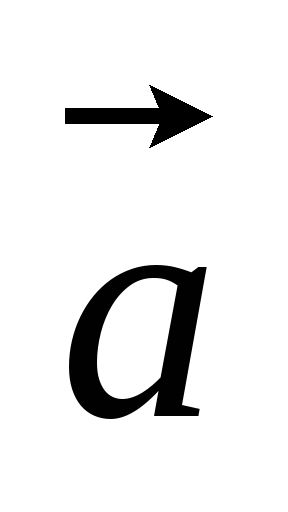 ,
, ,
,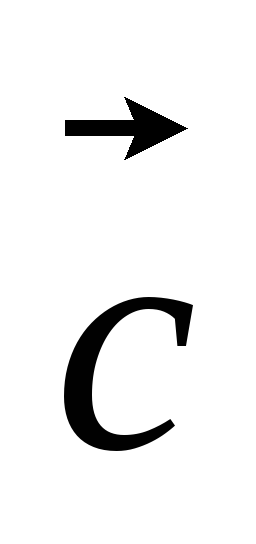 не существовать такие числа
не существовать такие числа иk,
что
иk,
что
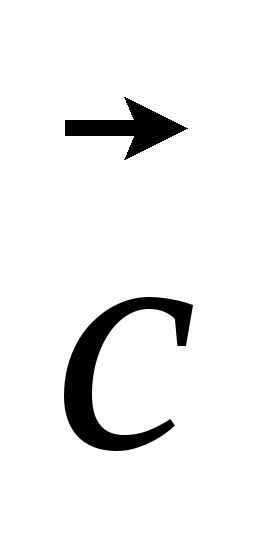 =
=
 +k
+k ?
?Даны векторы
 (1,2,3),
(1,2,3),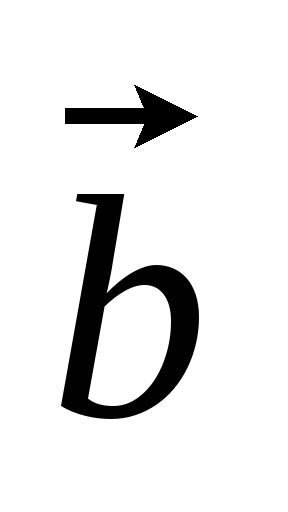 (2,-1,1),
(2,-1,1),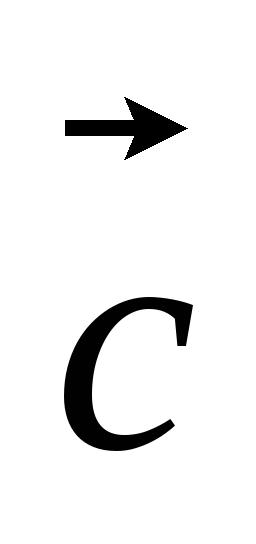 (3,1,-4)
и
(3,1,-4)
и (-1,8,7).
Доказать, что: а) векторы
(-1,8,7).
Доказать, что: а) векторы ,
,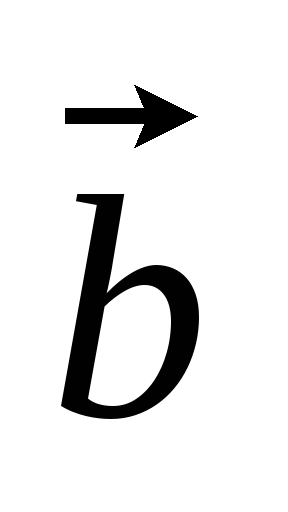 ,
,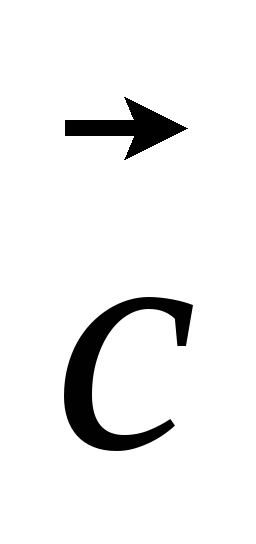 линейно независимы, б) вектор
линейно независимы, б) вектор принадлежит векторному подпространству,
натянутому на векторы
принадлежит векторному подпространству,
натянутому на векторы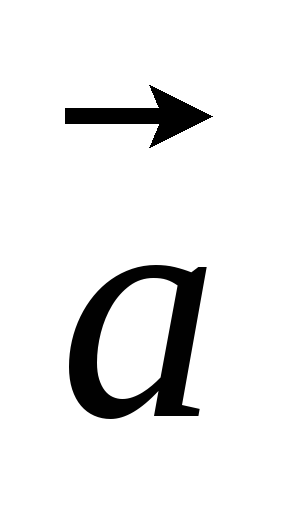 и
и .
.
